Тема 1.6. Задачі дробово-лінійного програмування

Загальний вигляд задачі. Загальна задача дробово-лінійного програмування полягає у визначенні максимального значення функції

(1.6.1)

при умовах

(1.6.2)

, (1.6.3)

де C_j, d_j, b_i та a_ij – деякі постійні числа,  (j = 1…n) і в області не-від’ємних розв’язків системи лінійних рівнянь (1.6.2). Будемо вважати, що .

Як і у випадку загальної задачі лінійного програмування, свого максимального значення цільова функція задачі (1.6.1)–(1.6.3) набуває в одній з вершин многогранника розв’язків, що визначається системою обмежень (1.6.2)–(1.6.3) (звичайно, при умові існування оптимального плану).

Розглянемо задачу, що полягає у визначенні максимального значення функції

(1.6.4)

при умовах

(1.6.5)

. (1.6.6)

Будемо вважати, що . Для знаходження розв’язку задачі (1.6.4)–(1.6.6) спочатку знаходимо многогранник розв’язків, визначений обмеженнями (1.6.5)–(1.6.6). Припускаючи, що цей многокутник не порожній, надаємо деякого значення h такого, що пряма лінія

, (1.6.7)

яка проходить через початок координат, має спільні точки з многогранником розв’язків. Обертаючи пряму (1.6.7) навколо початку координат, або визначаємо вершину (або вершини), в яких функція F набуває максимальних значень, або встановлюємо необмеженість функції на множині планів задачі.

Алгоритм розв’язування. Процес знаходження розв’язку конкретної задачі типу (1.6.4)–(1.6.6) включає такі етапи:

1. У системі обмежень задачі замінюють знаки нерівностей знаками рівностей і будують прямі, що визначаються отриманими рівняннями.

2. Знаходять півплощини, визначені кожною нерівністю системи обмежень задачі.

3. Знаходять многокутник розв’язків задачі.

4. Будують пряму (1.6.7), рівняння якої отримуємо при наданні цільовій функції деякого постійного значення.

5. Визначають точку максимуму або встановлюють відсутність розв’язку задачі.

6. Знаходять значення цільової функції в точці максимуму.

До розглянутого типу математичних моделей приводять економічні задачі, в яких необхідно «екстремізувати» питомі економічні показники, наприклад, собівартість, рентабельність та ін.

Задача. Для виробництва двох видів виробів А і В підприємство використовує три типи технологічного обладнання. Кожен з виробів повинен пройти обробку на кожному обладнанні. На І-му та ІІІ-му типах обладнання обробку можна проводити відповідно не більше 26 та 39 годин, а на ІІ-му типі – не менше 4 годин. Час, що витрачається на обробку одного виробу на різних типах обладнання вказаний у таблиці:

Тип обладнання	Витрати часу на обробку 1 виробу		Ресурс часу
	А	В
І ІІ ІІІ	2 1 12	8 1 3	26 4 39
Витрати на вироб-ництво 1-го виробу	2	3

Визначити, скільки виробів кожного виду треба встановити підприємству, щоб собівартість одного виробу була мінімальною.

Нехай х₁ – кількість виготовлених виробів виду А, х₂ – кількість виготовлених виробів виду В. Загальні витрати становитимуть 2х₁ + 3х₂, а собівартість .

Складемо систему обмежень:

Згідно з економічним змістом, х₁, х₂  0.

Для знаходження розв’язку задачі побудуємо многокутник розв’язків. Це трикутник BCD (рис.1.7).

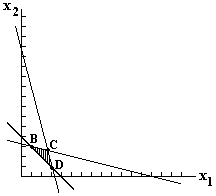
Рис.1.7.

Отже, функція F набуває екстремального значення в одній з трьох точок: B, C чи D. Для визначення конкретної точки мінімуму функції F надамо їй деякого значення, наприклад, 11/4. Тоді

або

.

Це рівняння визначає пряму, що проходить через початок координат. Координати точок, що належать цій прямій і многокутникові розв’язків, є планами задачі, при якій значення F дорівнює 11/4. В нашому випадку до вказаних точок належить лише точка В(1; 3).

Тепер нехай h = 5/2.

або

.

Це також пряма, що проходить через початок координат. Її можна розглядати, як пряму, отриману при обертанні попередньої прямої навколо початку координат.

Знайдемо останню спільну точку прямої з многокутником розв’язків. Це точка D(3; 1), в якій досягається мінімум функції F.

Отже, оптимальним планом виробництва продукції є план, згідно якого виготовлятимуть 3 вироби виду А і один виріб виду В. Собівартість одного виробу буде мінімальною й дорівнюватиме

.

Відзначимо, що при розв’язуванні деяких конкретних задач можуть реалізуватись різні випадки:

1. Многокутник розв’язків обмежений, тоді максимум і мінімум досягаються у кутових точках.

2. Многокутник розв’язків не обмежений, але існують кутові точки, в яких цільова функція задачі набуває відповідно максимального і мінімального значень.

3. Многокутник розв’язків не обмежений і один з екстремумів досягається. Наприклад, мінімум досягається в одній з вершин, функція F має так званий асимптотичний максимум.

4. Многокутник розв’язків не обмежений, і обидва екстремуми є асимптотичними.

Сформульована задача (1.6.4)–(1.6.6) може бути зведена до задачі лінійного програмування. Для цього вводять позначення

(1.6.8)

і нові змінні

. (1.6.9)

Застосовуючи нові змінні, вихідну задачу (1.6.4)–(1.6.6) приводять до такої: знайти максимум функції

(1.6.10)

при умовах

, (1.6.11)

, (1.6.12)

0, у₀  0. (1.6.13)

Задача (1.6.10)–(1.6.13) є задачею лінійного програмування, отже, її можна розв’язати відомими методами (наприклад, симплексним). Знаючи оптимальний план цієї задачі, на основі співвідношень (1.6.9) отримаємо оптимальний план вихідної задачі.

ІІ. НЕЛІНІЙНЕ ПРОГРАМУВАННЯ