
- •Розділ 3. Вступ у математичний аналіз § 1. Множини дійсних чисел
- •1.1. Сталі і змінні величини
- •1.2. Множини дійсних чисел
- •1.3. Абсолютна величина дійсного числа
- •Властивості абсолютної величини
- •1.4. Властивості абсолютної величини, зв’язаної з нерівностями величин. Окіл точки
- •1.5. Верхня і нижня грані дійсних чисел
- •§2. Класифікація функцій
- •2.1. Поняття функції. Способи задання функції
- •2.2. Класифікація функцій
- •2.3. Криві попиту і пропозиції. Точка рівноваги
- •§ 3. Границя числової послідовності
- •3.1. Числова послідовність
§2. Класифікація функцій
2.1. Поняття функції. Способи задання функції
Означення
1.
Нехай
![]() і
і
![]() - дві числові множини. Якщо кожному
значенню
за деяким правилом (законом)
- дві числові множини. Якщо кожному
значенню
за деяким правилом (законом)
![]() поставимо
у відповідність одне дійсне число
поставимо
у відповідність одне дійсне число
![]()
,
то будемо говорити , що на множині
задано функцію
.
,
то будемо говорити , що на множині
задано функцію
.
Множина
![]() називається областю визначення
називається областю визначення
функції,
а множина
![]() - називається областю значень
функції, х
– називається аргументом функції.
- називається областю значень
функції, х
– називається аргументом функції.
Функції позначаються малими буквами латинського
алфавіту
![]() і т.д.
і т.д.
Але
для простоти вивчення курсу вищої
математики надалі ми будемо використовувати
такі формулювання і позначення функцій:
нехай задано функції
![]() і
т.д.
і
т.д.
Основними способами задання функції є такі: аналітичний, табличний, графічний, словесний.
Функція, задана аналітично, якщо вона задана за допомогою однієї або кількох формул. Табличний спосіб полягає в тому, що функцію задають за допомогою таблиці, яка містить ряд окремих значень аргументу і відповідні їм значення функції.
Графічний
спосіб задання функції полягає в тому,
що її подають на малюнку у вигляді певної
кривої, що задає множину точок
![]() ,
яку називають графіком функції.
,
яку називають графіком функції.
Якщо функцію не можна задати першими трьома способами, то її описують за допомогою висловлень (опису). В цьому полягає словесний спосіб задання функції.
2.2. Класифікація функцій
а) Обмежені функції:
Означення
2. Функція
![]() ,
яка визначена на множині
називається
обмеженою зверху (знизу), якщо існує
число
,
яка визначена на множині
називається
обмеженою зверху (знизу), якщо існує
число
![]() таке, що для всіх
виконується нерівність
таке, що для всіх
виконується нерівність
![]() (
(![]() ).
).
Якщо функція , обмежена на множині і зверху і знизу, то вона називається обмеженою на всій множині .
Наприклад,
функція
![]() обмежена на всій числовій осі,
обмежена на всій числовій осі,
![]() для
(
для
(![]() .
.
б) Монотонні функції:
Означення
3.
Функція
,
яка визначена на множині
називається:
а) зростаючою;
б) спадною;
в) незростаючою;
г) неспадною на цій
множині, якщо для будь-яких
![]() і
і
![]() ,
які належать множині
і при
<
мають місце відповідні нерівності :
а)
,
які належать множині
і при
<
мають місце відповідні нерівності :
а)
![]() б)
б)![]() в)
в)![]()
г)
![]()
Функції, які задовольняють даному означенню, називають монотонними.
в) Парні і непарні функції:
Означення
4.
Функція
називається парною, якщо для будь-яких
=![]() виконується умова
виконується умова
![]() і непарною, якщо
і непарною, якщо
![]()
Наприклад,
![]() - парна функція,
- парна функція,
![]() -
непарна функція. Зауважимо,
що графік парної функції симетричний
відносно осі
-
непарна функція. Зауважимо,
що графік парної функції симетричний
відносно осі
![]() ,
а графік непарної функції
- симетричний
відносно початку координат.
,
а графік непарної функції
- симетричний
відносно початку координат.
г) Періодичні функції:
Означення
5.
Функція
,
яка визначена на всій числовій осі
називається періодичною, якщо існує
таке число
![]() яке називається періодом, що має місце
нерівність
яке називається періодом, що має місце
нерівність
![]() для всіх x
для всіх x![]()
Наприклад,
![]()
Функція
![]() є періодична з періодом
є періодична з періодом
![]() .
.
д) Складні функції:
Означення
6.
Нехай
функція
![]() визначена на множині
визначена на множині
![]() ,
а функція
,
а функція![]() визначена на множині
і всі її значення
визначена на множині
і всі її значення
![]()
.
Тоді змінна
.
Тоді змінна
![]() через проміжну змінну
є
функцією
:
через проміжну змінну
є
функцією
:
![]() В цьому випадку
є складною функцією або функцією від
функції.
В цьому випадку
є складною функцією або функцією від
функції.
Наприклад,
![]() ,
,
![]() Тоді
Тоді
![]() є складною функцією
.
є складною функцією
.
е) Обернені функції:
Нехай
функція
задана на множині
,
а множина значень (область зміни функції
) є
![]() .
Якщо кожному значенню
.
Якщо кожному значенню
![]() відповідає одне значення
,
для якого
,
то на множині
можна визначити функцію
відповідає одне значення
,
для якого
,
то на множині
можна визначити функцію
![]() так,
що кожному значенню
буде відповідати одне значення
,
для якого
так,
що кожному значенню
буде відповідати одне значення
,
для якого
![]()
Функція називається оберненою відносно
функції , яка задовольняє для всіх умові
![]()
Приклад.
Нехай задана функція
,
![]()
![]()
![]() .
Оберненою для даної функції буде функція
.
Оберненою для даної функції буде функція
![]()
![]() =
.
=
.
є) Неявна функція від однієї змінної.
Якщо
функція задана не рівнянням вигляду
,
а рівнянням вигляду
![]() ,
то у припущенні, що на деякій множині
рівняння
має єдиний розв’язок
,
то у припущенні, що на деякій множині
рівняння
має єдиний розв’язок
![]() , тоді рівність
називають неявним заданням функції.
, тоді рівність
називають неявним заданням функції.
Наприклад,
,
![]() - явні функції, а рівняння
- явні функції, а рівняння
![]() визначає неявну функцію
від
.
визначає неявну функцію
від
.
ж) Елементарні функції.
Cтепенева
функція
![]() ,
показникова
,
показникова
![]() ,
логарифмічна
,
логарифмічна
![]() ,тригонометричні
,тригонометричні
![]() ,
,
![]() ,
,
![]() ,
обернені тригонометричні
,
обернені тригонометричні
![]()
![]() ,
,
![]() ,
,
![]() і стала
і стала
![]() називаються основними елементарними
функціями.
називаються основними елементарними
функціями.
Означення
7.
Основні
елементарні функції, а також функції,
знайдені за допомогою формул, що містять
лише скінчене число арифметичних дій
(+,-,![]() )
і суперпозицій основних елементарних
функцій, називаються елементарними
функціями.
)
і суперпозицій основних елементарних
функцій, називаються елементарними
функціями.
Наприклад,
![]() - елементарна функція.
- елементарна функція.
Елементарні функції поділяються на такі класи:
1)Цілі раціональні функції:
Цілі
раціональні функції – це функції вигляду
![]() ,
де
,
де
![]() сталі
дійсні числа. Такі функції називаються
ще многочленами, а числа
сталі
дійсні числа. Такі функції називаються
ще многочленами, а числа
![]() - коефіцієнтами многочлена;
якщо
- коефіцієнтами многочлена;
якщо
![]() ,
то число
,
то число
![]() називають степенем многочлена.
називають степенем многочлена.
2) Раціональні функції:
Раціональні функції – це функції вигляду
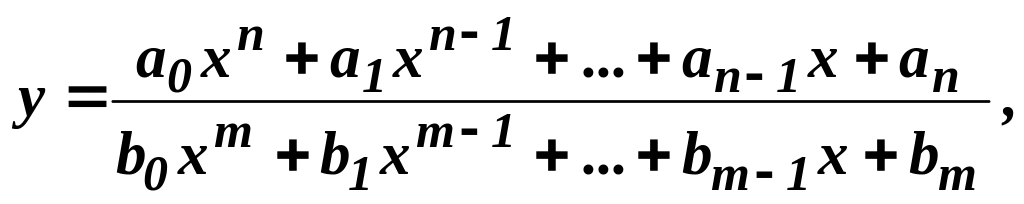 тобто
це частка двох цілих
тобто
це частка двох цілих
раціональних функцій (многочленів).
Якщо
![]() ,
,
![]() ,
то раціональна функція називається
дробово-раціональною.
,
то раціональна функція називається
дробово-раціональною.
3)Ірраціональні функції:
Ірраціональні
функції - це функції, які задані за
допомогою суперпозицій раціональних
функцій, степеневих функцій з раціональними
показниками і чотирьох арифметичних
дій, застосованих скінчене число раз.
Наприклад,
![]() - ірраціональна функція .
- ірраціональна функція .
4) Алгебраїчні функції:
Функція
від
(![]() називається алгебраїчною, якщо вона
задовольняє рівняння
називається алгебраїчною, якщо вона
задовольняє рівняння
![]() де
Pk(x),(
де
Pk(x),(![]() - алгебраїчні многочлени від
.
- алгебраїчні многочлени від
.
Всяка
раціональна функція є алгебраїчною,
оскільки
![]() ,
де
,
де
![]()
![]()
5)Трансцендентні функції:
Елементарні функції, які не є алгебраїчними, називаються трансцендентними елементарними функціями. Можна показати, що тригонометричні, обернено тригонометричні, показникова і логарифмічна функції є трансцендентними елементарними функціями.
6) Деякі неелементарні функції:
1.![]() - абсолютне значення, або
- абсолютне значення, або
м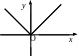 одуль,числа
одуль,числа
2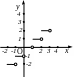 .
.![]() – ціла
частина числа
– ціла
частина числа
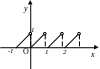
3.![]() – дробова
частина
числа
– дробова
частина
числа

4.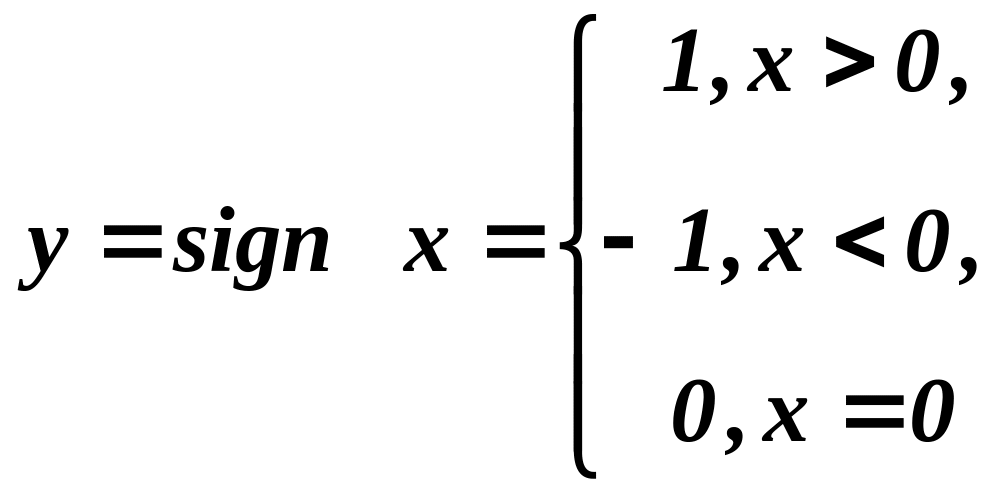
- знак числа
