1.3. Абсолютна величина дійсного числа

Означення 2. Абсолютною величиною (або модулем) дійсного числа називається саме число , якщо додатне і число - , якщо від’ємне. Абсолютна величина приймається рівною 0 і позначають

Наприклад, .

• Властивості абсолютної величини

1. Абсолютна величина алгебраїчної суми не більша суми абсолютних величин , тобто

2. Абсолютна величина добутку дорівнює добутку абсолютних величин множників :

3. Абсолютна величина частки дорівнює частці від ділення абсолютних величин діленого і дільника : , якщо .

4. Для будь-якого правильні співвідношення:

1.4. Властивості абсолютної величини, зв’язаної з нерівностями величин. Окіл точки

1. Нехай . Нерівність рівносильна нерівностям .

2. Нехай . Нерівність рівносильна

нерівностям .

Означення 3. Околом точки називається кожен інтервал вигляду ( ), де .

Таким чином, запис , , означає множину чисел , що знаходяться в околі точки .

1.5. Верхня і нижня грані дійсних чисел

Нехай дано непорожню множину дійсних чисел ( Множина називається обмеженою зверху (знизу), якщо існує дійсне число таке, що для всіх є правильна нерівність .

Число при цьому називається верхньою (нижньою) межею множини . Зрозуміло, що коли -верхня (нижня) межа множини , то будь-яке число також буде верхньою (нижньою) межею.

Означення 4. Найменша верхня межа непорожньої обмеженої зверху множини дійсних чисел називається точною верхньою межею або верхньою гранню цієї множини і позначається sup .

Означення 5. Найбільша нижня межа непорожньої обмеженої знизу множини дійсних чисел називається точною нижньою межею або нижньою гранню цієї множини і позначається inf .

Наприклад, якщо , то sup =1, inf =0.

Тут верхня грань, яка дорівнює 1, належить множині а нижня грань, яка дорівнює 0, множині не належить. Коли у множині є найбільше (найменше) число , тобто таке число  , що будь-яке число  задовольняє нерівність

, то це число й буде верхньою (нижньою) гранню множини . Однак не в усякій непорожній обмеженій зверху (знизу) множині дійсних чисел є найбільше (найменше ) число. Наприклад, у розглянутій вище множині є найбільше число, але немає найменшого, а у множині немає ні найменшого, ні найбільшого числа.

Сформулюємо без доведення наступне твердження.

ТЕОРЕМА 1. У будь-якої непорожньої обмеженої зверху (знизу) множини дійсних чисел існує верхня (нижня) грань.

Надалі нам доведеться часто користуватися наступними двома властивостями sup і inf .

Властивість 1 . Якщо - непорожня обмежена зверху множина дійсних чисел і , то для будь-якого  правильна нерівність і для будь-якого числа існує число  таке, що

В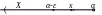 ластивість 2 . Якщо - непорожня обмежена знизу множина дійсних чисел і , то

1) для будь-якого  правильна нерівність ;

2) для будь-якого числа

існує число  таке, що

З азначимо, що коли множина дійсних чисел необмежена зверху (знизу), то за означенням