17.2. Рівняння площини у відрізках

Нехай в рівнянні (2.72) кожний із коефіцієнтів не дорівнює нулю, тобто площина перетинає всі осі координат і не проходить через початок координат. Перетворимо рівняння (2.72) таким чином:

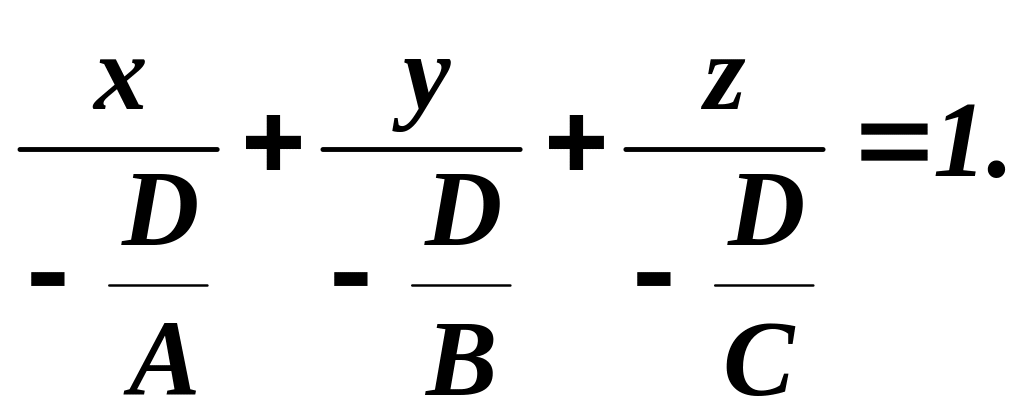
Для скорочення запису позначимо тоді рівняння площини буде мати вигляд

. (2.73)

Рівняння (2.73) називають рівнянням площини у відрізках, де числа є величини відрізків, які відтинає площина на осях координат.

17.3. Кут між двома площинами. Умови паралельності

і перпендикулярності площин.

Нехай задано дві площини

, (2.74)

. (2.75)

Якщо ці площини перетинаються, то кутом між ними назвемо будь-який суміжний двогранний кут. Один із них дорівнює куту між векторами і , а другий - .

Значить, шуканий кут φ можна знайти за формулою (2.21) §11

. (2.76)

Якщо то із формули (2.76) одержуємо, що

. (2.77)

Умова (2.77) одержується із умови перпендикулярності векторів і . Рівність (2.77) називається умовою перпендикулярності двох площин.

Якщо площини (2.74) і (2.75) паралельні, то нормалі цих площин і будуть колінеарні і тоді за

формулою (2.23) одержимо

. (2.78)

Умова (2.78) виражає умову паралельності двох площин.

Приклад 1. Записати рівняння площини, що проходить через точки і і перпендикулярна до площини .

Розв’язування. Тому що площина проходить через точку , то її координати задовольняють рівняння (2.71), тобто

. (2.79)

Аналогічно, площина проходить і через точку , то її координати задовольняють рівнянню (2.79), тобто

. (2.80)

Використаємо умову перпендикулярності (2.77) для площини (2.79) і заданої площини 3x+5y-7z+21=0, тобто 3A+5B-7C=0. Для знаходження А,В,С маємо систему двох рівнянь з трьома невідомими, а саме

З даної системи знаходимо і через , тобто і підставляємо одержані значення в рівняння (2.79):

Зробивши спрощення в останньому рівнянні , одержуємо шукане рівняння площини 3x+y+2z-23=0.

17.4. Нормальне рівняння площини

Положення площини в просторі можна визначити через нор-

мальний вектор , початок якого співпадає з початком коор-

динат, а кінець знаходиться на площині π. Нехай довжина цього ве-

ктора дорівнює , тобто , а кути нахилу цього вектора з осями координат є α,β,γ (мал.45). Значить р є віддаль площини до

144