§17. Площина та її рівняння

Нехай в системі координат задана довільна площина .

Візьмемо на цій площині яку-небудь точку Виберемо вектор перпендикулярний до площини і

н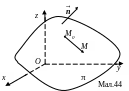 азвемо його нормальним вектором, або просто нормаллю. Цими двома величинами (точкою через яку проходить площина і вектором перпендикулярним до площини) площина визначається однозначно. На площині візьмемо довільну точку (мал.44). Тому що точка знаходиться на площині, то вектор перпендикулярний до вектора , а це значить, що їх скалярний добуток дорівнює нулю, тобто (2.70).

Рівняння (2.70) є векторним рівнянням площини. Розпишемо рівняння (2.70) в координатній формі , знаючи, що . Одержимо

(2.71).

Рівняння (2.71) є рівнянням площини, що проходить через задану точку і перпендикулярна до заданого вектора . Рівняння (2.71) задовольняють координати довільної точки, яка знаходиться на цій площині і не задовольняють координати довільної точки, яка не знаходиться на цій площині.

Розкривши дужки в рівнянні (2.71), одержимо

(2.72)

де . Рівняння (2.72) називається загальним рівнянням площини. Кожна площина в декартових прямокутних координатах визначається рівнянням першого степеня відносно біжучих координат Вірно і обернене твердження: кожне рівняння першого степеня відносно біжучих координат визначає

площину.

Дійсно, нехай - який –небудь розв’язок рівняння (2.72), тобто

. (2.73).

Віднімаючи почленно із рівняння (2.72) рівність (2.73), одержимо рівняння яке і є рівнянням площини, що проходить через точку і перпендикулярна до вектора .

17.1. Дослідження загального рівняння площини

Під дослідженням загального рівняння площини розуміється те, яке положення займає площина, коли деякі із коефіцієнтів і перетворюються в нуль.

1) , то рівняння площини має вигляд тобто площина проходить через початок координат;

2) то рівняння (2.72) буде мати вигляд .

В площині це рівняння визначає пряму лінію, а в просторі це буде рівняння площини паралельної вісі

3) , то рівняння (2.72) буде мати вигляд .

і є рівнянням площини, паралельної вісі

4) то рівняння (2.72) має вигляд і є рівнянням площини , яка паралельна вісі . Отже, якщо в рівнянні площини (2.72) відсутня одна із координат або то площина паралельна вісі або .

5) Якщо , то рівнянню відповідає площина, яка проходить через початок координат і паралельна вісі , тобто ця площина проходить через вісь ;

6) Аналогічно, коли , , то рівнянню відповідає площина , що проходить через вісь .

7) Коли , то рівнянню відповідає площина, що проходить через вісь .

8) Якщо , то рівняння визначає площину , яка паралельна вісі і вісі , тобто площина паралельна координатній площині . Ця площина відтинає на осі відрізок .

9) Аналогічно, коли , то рівняння визначає площину , яка паралельна координатній площині і відтинає на вісі відрізок

10) Коли , , то рівняння визначає площину, яка паралельна координатній площині і відтинає на вісі відрізок .

11) Якщо то рівняння рівносильне , а це і є рівняння координатної площини .

12) Аналогічно, коли , то рівняння ( ) представляє відповідно координатну площину

13) Якщо то рівняння (або є відповідно рівнянням координатної площини Oxy.