§15. Квадратичні форми.
Означення.
Квадратичною формою
від
змінних називається сума, кожен член якої є або квадратом однієї із змінних, або добутком двох різних змінних, взятих з
деяким коефіцієнтом, тобто
.
(2.44)
Допускаємо, що в квадратичної форми (2.44) - дійсні числа.
Розпишемо квадратичну
форму (2.44), розбивши доданки, що містять
добутки змінних на дві рівні частини
Матриця
,
(2.45)
або
є
симетричною, так як
,
називається матрицею квадратичної
форми (2.44).
Рангом квадратичної форми називається ранг її матриці. Квадратична форма називається невиродженою, якщо її матриця невироджена.
Якщо
,
то квадратичну форму можна переписати
в матричному вигляді
.
Вираз
представляє собою квадратичну форму в
матричному вигляді.
Приклад 1. Записати
в матричному вигляді квадратичну форму
Розв'язування. Матриця даної квадратичної форми має вигляд
.
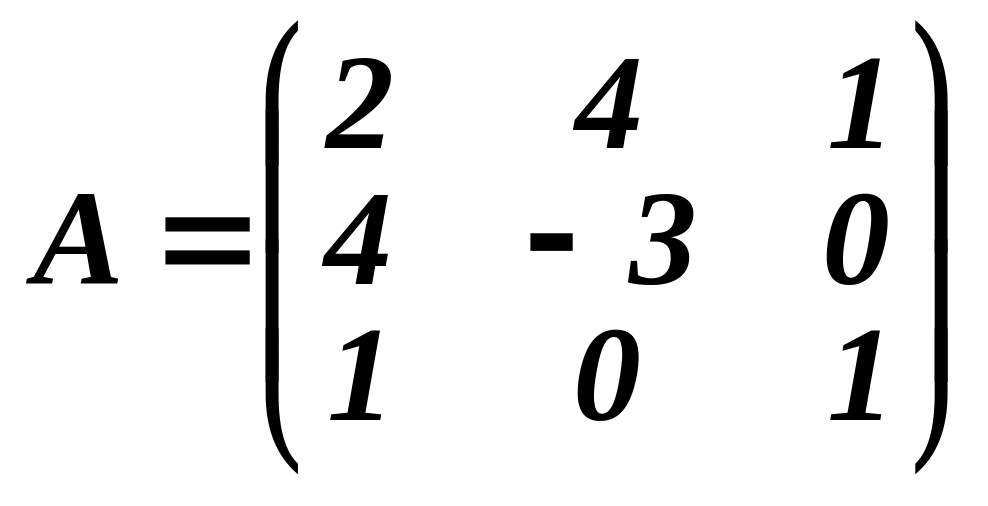Значить
Квадратична форма
називається канонічною (або другими
словами має канонічний вигляд), якщо
всі
коли
.
Тоді
квадратична форма буде мати вигляд
.
Розглянемо таку теорему.
ТЕОРЕМА 1. Довільна квадратична форма приводиться до канонічного вигляду.
Доведення.
Нехай задана квадратична форма (2.44) з
матрицею (2.45) в базисі
Так як
симетрична
матриця, то існує ортогональна матриця
така, що
Матриця є матрицею переходу від базису
,
(2.46)
до деякого базису
.
(2.47)
Примітка. Дійсна
квадратна матриця називається
ортогональною, якщо сума квадратів
елементів кожного стовпчика дорівнює
одиниці і сума добутків відповідних
елементів із двох різних стовпчиків
дорівнює нулю. Необхідна і достатня
умова ортогональності матриці
є
умова
Нехай
і
є
вектори- стовпчики із координат вектора
відповідно в базисах (2.46) і (2.47). Тоді
і
або
.
(2.48)