§14. Власні числа та власні вектори матриці

Означення. Вектор називається власним вектором матриці , якщо знайдеться таке число що

, (2.36)

де число називається власним значенням матриці , яке відповідає вектору

Запишемо рівність (2.36) в матричній формі:

, (2.37)

де матриця-стовпчик із координат вектора .

Рівняння (2.37) розпишемо в координатній формі

(2.38)

Перепишемо рівняння системи (2.38) так, щоб в правих частинах були нулі:

(2.39)

Щоб перейти до розгляду системи (2.39) доведемо таку теорему.

ТЕОРЕМА. Однорідна система ( рівнянь з невідомими)

(2.40)

має ненульовий розв’язок тоді і тільки тоді, коли , тобто коли матриця є виродженою.

Доведення. Нехай система (2.40) має ненульовий розв’язок. Покажемо, що . Дійсно, якщо б це було не так, тобто , то розв’язуючи систему за правилом Крамера, ми б одержали єдиний нульовий розв’язок , а це протирічить умові.

Нехай , покажемо, що існує ненульовий розв’язок системи. Для зручності розглянемо систему двох рівнянь.

(2.41)

Тому що , то і , тобто матриця є виродженою.Значить стрічки матриці є лінійно залежними, а це означає, що і стовпчики матриці є лінійно залежні. Вказані стовпчики позначимо через . При цьому існують такі числа і , які не дорівнюють одночасно нулю, що виконується рівність або в координатній формі .

Отже, це значить, що система (2.41) має ненульовий розв’язок. Теорема доведена.

Тепер повернемось до системи (2.39). На основі вище приведеної теореми, система (2.39) має ненульовий розв’язок тоді і тільки тоді, коли визначник системи дорівнює нулю, тобто

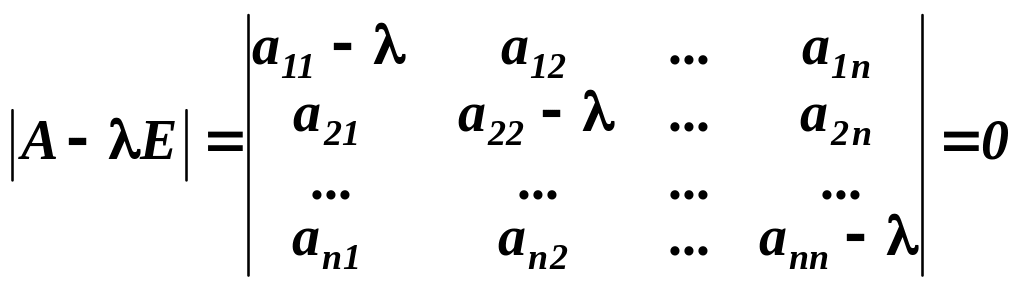. (2.42)

Визначник (2.42) є многочленом -го степеня відносно . Цей многочлен називається характеристичним многочленом матриці А, а рівняння (2.42) називається характеристичним рівнянням матриці А

Приклад 1. Знайти власні числа і власні вектори матриці

.

Розв’язування. Запишемо систему типу (2.39) для знаходження власних чисел і власних векторів, а саме

(2.43)

Як нам уже відомо, для того, щоб ця система мала ненульові розв’язки, потрібно , щоб визначник цієї системи дорівнював нулю, тобто або Корені цього квадратного рівняння є Таким чином ми знайшли власні (характеристичні) числа.

Тепер знайдемо власні вектори, які відповідають знайденим власним числам.

Щоб знайти координати власного вектора, що відповідає власному числу то підставляємо в систему (2.43).

Одержимо , звідси , при довільному , є розв’язком цієї системи. Отже, вектор , є власним вектором-стовпчиком матриці

Для знаходження координат власного вектора матриці що відповідає власному числу поступаємо аналогічно. Число підставляємо в систему (2.43) і одержимо

звідси

Значить, , , а вектор-стовпчик є власним вектором, що відповідає власному числу .

14.1. Лінійна модель торгівлі.

Одним із прикладів економічних процесів, які приводять до поняття власного числа і власного вектора матриці, є процес взаємних закупок товарів. Ми будемо розглядати лінійну модель обміну, або як її називають другими словами, модель міжнародної торгівлі.

Нехай є держав, національний дохід яких дорів-

нює відповідно . Долю національного доходу, яку держава витрачає на покупку товарів у держави позначимо коефіцієнтами . Будемо вважати, що весь національний дохід витрачається на закупку товарів або всередині держави, або на імпорт із інших держав, тобто

.

Розглянемо матрицю коофіцієнтів :

Матриця А, з властивістю, що сума елементів її довільного стовпчика дорівнює 1, називається структурною матрицею торгівлі.

Для будь-якої держави загальна виручка від зовнішньої і внутрішньої торгівлі складає

Для збалансованості торгівлі необхідно бездефіцитність торгівлі кожної держави, тобто виручка від торгівлі кожної держави не повинна бути меншою від її національного доходу, тобто або В цій умові не може бути знака нерівності. Дійсно, додавши всі ці нерівності, коли міняється від 1 до і згрупувавши, одержимо

Тому що в дужках є суми елементів матриці по

стовпчиках, які дорівнюють 1, ми отримали суперечливу нерівність. Отже, можливий тільки знак рівності.

Введемо вектор національних доходів

держав, одержимо матричне рівняння або (A-E)X=0, де - матриця-стовпчик із координат вектора

Значить задача звелася до знаходження власного вектора матриці A, який відповідає власному значенню λ=1.

Приклад 1.Структурна матриця торгівлі трьох країн

має вигляд

.

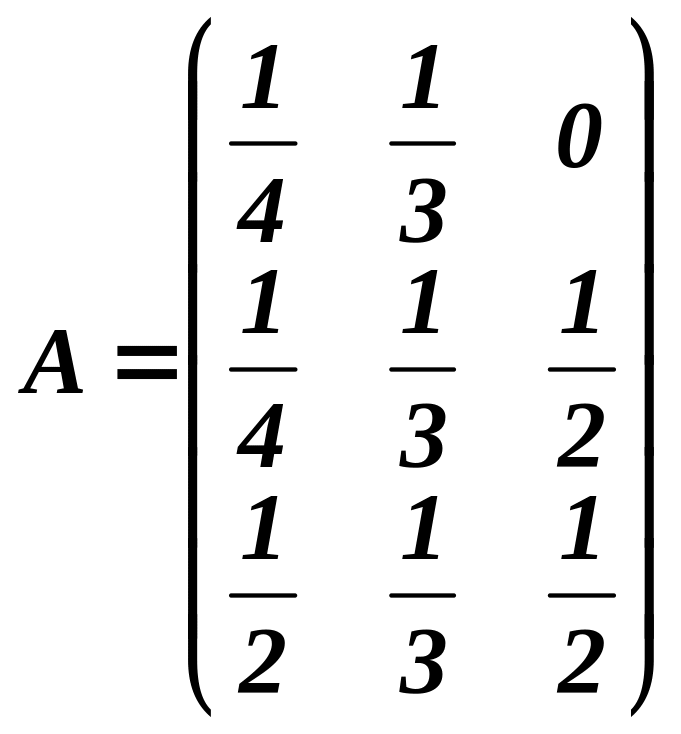Знайти співвідношення між національними доходами країн, при якому буде торгівля збалансована.

Розв’язування. Знаходимо власний вектор який відповідає власному значенню розв’язавши рівняння або систему рівнянь

Позначимо національні доходи відповідно Тоді будемо шукати власний вектор , який відповідає власному значенню λ=1 розв’язавши рівняння (A-E)X=0.

Тому що ранг даної системи дорівнює 2, то одна із змінних, наприклад x₃=C є вільною невідомою. Решту невідомих виразимо через неї. Розв’язуючи дану систему, знаходимо, що

тобто

Одержаний результат означає, що збалансованість торгівлі

трьох країн досягається при векторі національного доходу тобто при співвідношенні доходів або