3.2.Определение коэффициентов, входящих в эмпирическую формулу

После того, как установлена пригодность выбранной формулы для выражения изучаемой зависимости переменных, необходимо определить численные значения входящих в формулу коэффициентов. Наиболее точные результаты дает использование метода наименьших квадратов.

Однако этот способ громоздок и во многих случаях его можно заменить более простым способом средних, дающих вполне удовлетворительные результаты.

Способ средних заключается в следующем: использовав метод выравнивания и получив линейную зависимость

Y=A+b·X,

(6)

составляют условные уравнения Y_i=A+B·X_i, число которых равно числу имеющихся соответственных значений X_i, Y_i.Условные уравнения разбивают на две приблизительно равные группы и уравнения, входящие в каждую из этих групп, складывают.

Получают два уравнения:

;

(7)

из которых находят неизвестные коэффициенты А и В.

Наиболее простым способом получения коэффициентов эмпирических формул, однако и наименее точным, является графический метод (метод натянутой нити).Он основан на геометрическом подборе прямой на глаз.С помощью соответствующей замены линеаризуют функциональную зависимость и получают линейную функцию вида

Y=A+B·X.

Нанеся полученные экспериментальные значения на соответствующие функциональные шкалы, подбирают графически прямую(рисунок 2), ближе всего подходящую к полученным значениям.

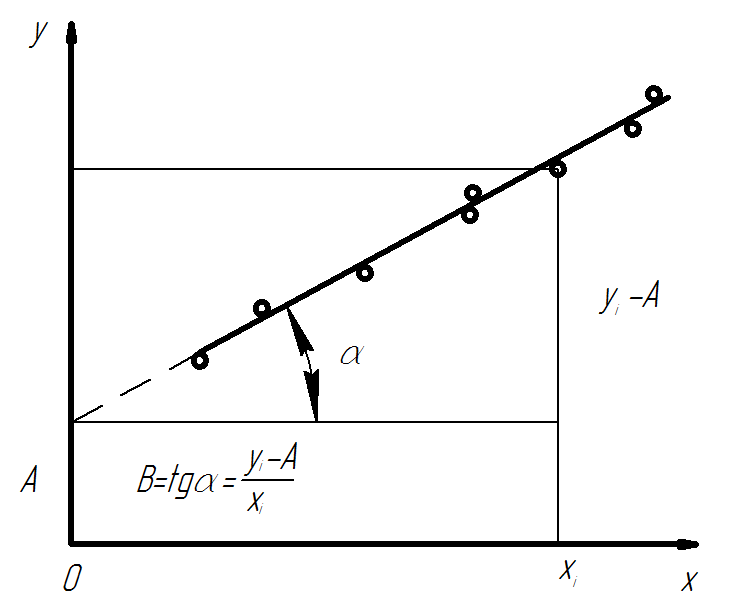
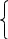
Рисунок 2 – Графическое определение коэффициентов эмпирических формул

Метод графического определения коэффициентов А и В понятен из рисунка 2.

Обратный переход к исходной функциональной зависимости осуществляется с учетом использованного метода линеаризации.

Если полученная прямая расположена далеко от начала координат и ее невозможно продолжить(рисунок 2), то используют следующие соотношения:

,	(8)
,	(8а)

где Y₁, X₁,Y₂,X₂– численные значения координат двух произвольных точек полученной прямой.

Рассмотрим теперь некоторые примеры применения этих двух способов.

ПРИМЕРI.В результате экспериментов получены значения перепадов давления ΔP, Па в функции от скорости воздуха υ, м/с, в отверстиях ситчатой тарелки, приведенной в таблице 3.

Найти зависимость перепада давления от скорости воздуха.

Таблица 3 – Значение перепада давления ΔPв зависимости от скорости воздуха υ

Экспериментальные значения величин				Вычисленные значения величин по
				по уравнению 12			по уравнению 13
ΔP, Па	υ, м/с	Lgυ	lgΔP	ΔP, Па	Δ, %	ΔP, Па		Δ, %
3	5,01	0,6998	0,4771	3,02	+0,7	3,05		+1,7
6	7,1	0,8513	0,7781	6,17	+2,8	6,12		+2,0
10	9,10	0,9590	1,0000	10,24	+2,4	10,05		+0,5
15	11,10	1,0453	1,1761	15,38	+2,6	14,96		-0,4
24	14,20	1,1523	1,3892	25,45	+3,9	24,45		-0,2
34,5	17,00	1,2304	1,5378	36,77	+6,6	35,08		+1,7
46,0	19,20	1,2833	1,6627	47,16	+2,7	44,75		-2,7
60,0	22,30	1,3485	1,3485	64,05	+5,3	60,37		+0,6
75,3	24,80	1,3945	1,3945	79,59	+5,7	74,67		-0,8
98,0	28,60	1,4564	1,4564	106,53	+8,6	99,30		+1,3

По экспериментальным данным строят график (в обычных координатах), представленный на рисунке 3.

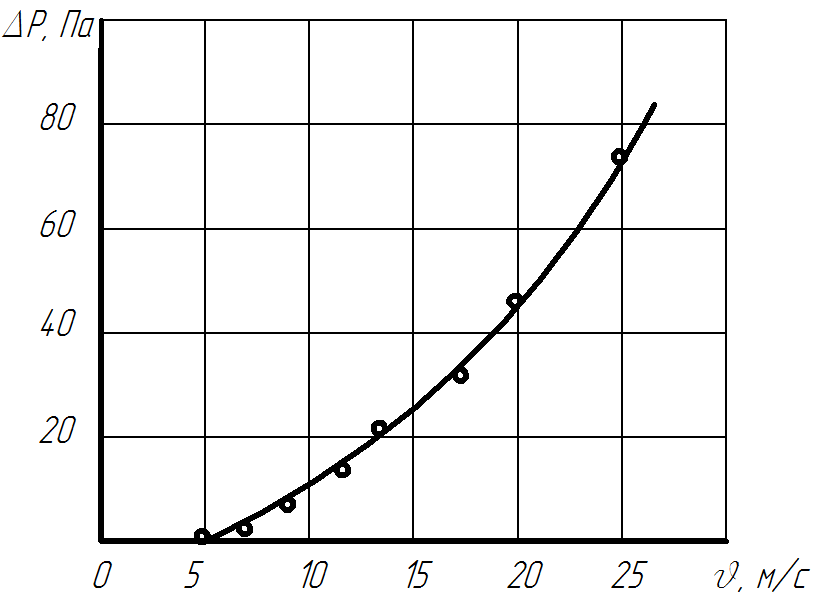
Рисунок 3 – Зависимость перепада давления ΔP от скорости воздуха υ (уравнение 9) в обычных координатах

Из уравнения полученной кривой с кривыми, приведенными в таблице 2, видно, что ее можно аппроксимировать уравнением 1, т.е. зависимость потери напора ∆Р от скорости газа υ описывается уравнением вида

∆P=aVb

(9)

Обозначим ∆Р=у и V=х. Путем логарифмирования линеаризуем уравнение (9)

lgy=lga+b·lgx

(10)

или

Y=A+BX.

(11)

В соответствии с уравнением(11) полученные экспериментальные данные изобразятся в логарифмических координатах в виде прямой, как это действительно видно из рисунка 4.

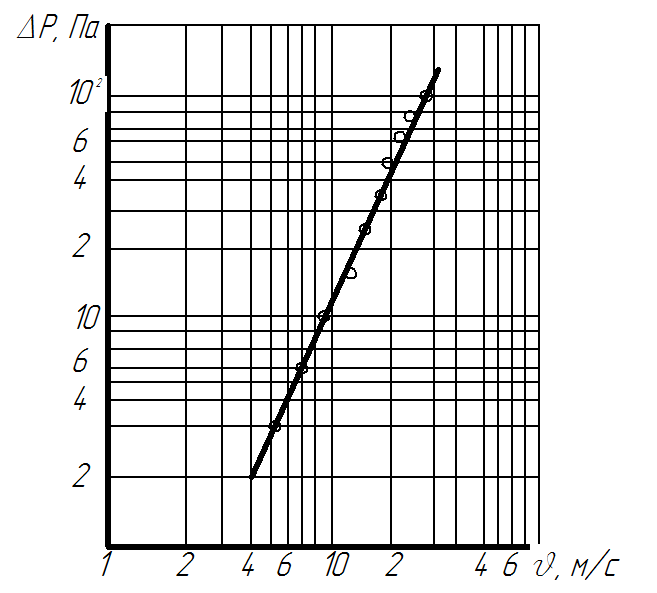
Рисунок 4 – Зависимость перепада давления ΔP от скорости воздуха υ (уравнение 9) в логарифмических координатах

Постоянные а и b определим графическим методом и методом средних.

Графический метод. Продолжив на рисунке 4 экспериментальную прямую до пересечения с осью координат, получим при Х=0 значение а=0,112 (А=-0,951).Постоянную b (угловой коэффициент прямой) находят построением, показанным на рисунке 4 пунктирными линиями в соответствии с уравнением 8а.

b=

Таким образом, при использовании графического метода получаем следующее уравнение

∆Р=0,112V2,045

(12)

Метод средних. Подставив в уравнение (11) значения величин, соответствующих экспериментальным данным из таблицы 3, получим следующие уравнения:

0,4771=А+0,6998В 1,5378=А+1,2304В

0,7781=А+0,8512В 1,6627=А+1,2633В

1,0000=А+0,9590В 1,7781=А+1,3483В

1,1760=А+1,0453В 1,8767=А+1,3944В

1,3691=А+1,1522В 1,9912=А+1,4563В

Разделив эти уравнения на две группы и сложив уравнения каждой группы, получаем систему двух уравнений:

4,8203=5А+4,7075В

8,8465=5А+6,7127В

решая ее, получаем:

В=в=2;

А=lga=-0,9158=1,0842;

а=0,1214

Подставив эти значения в уравнение (9), найдем выражение для определения потери напора в отверстиях ситчатой тарелки в зависимости от скорости воздуха в отверстиях

р=0,1214V2

(13)

В правой части таблицы 3 приведены значения ∆р, вычисленные по эмпирическим уравнениям 12 и 13, а также отклонения расчетных значений величин в % от значений полученных экспериментально.

Как видно из таблицы 3, уравнение 13, полученное методом средних, является значительно более точным.

ПРИМЕР 2.При конвективной сушке молочного сахара в псевдоожиженном состоянии получены следующие данные:

τс	0	20	40	60	80	100
ωc	29,5	18,4	11,9	8,5	5,0	3,3

где τ_с– продолжительность сушки,с;

ω^c– влажность, рассчитанная на сухой остаток,%.

Найти эмпирическую формулу, связывающую приведенные выше экспериментальные данные.

Переводя полученные экспериментальные данные на простые прямоугольные координаты, по форме кривой мы получаем возможность подобрать функциональные шкалы (вид уравнения), в которых данные эксперимента расположатся вдоль прямой линии. То есть специальным подбором функциональных шкал исходный криволинейный график преобразуется к прямолинейному типу.

На рисунке 5 изображен график зависимости ω^c=f(τ_с)(сплошная кривая) и экспоненциальная зависимость вида ω^c=ае^nτ(штриховая кривая).

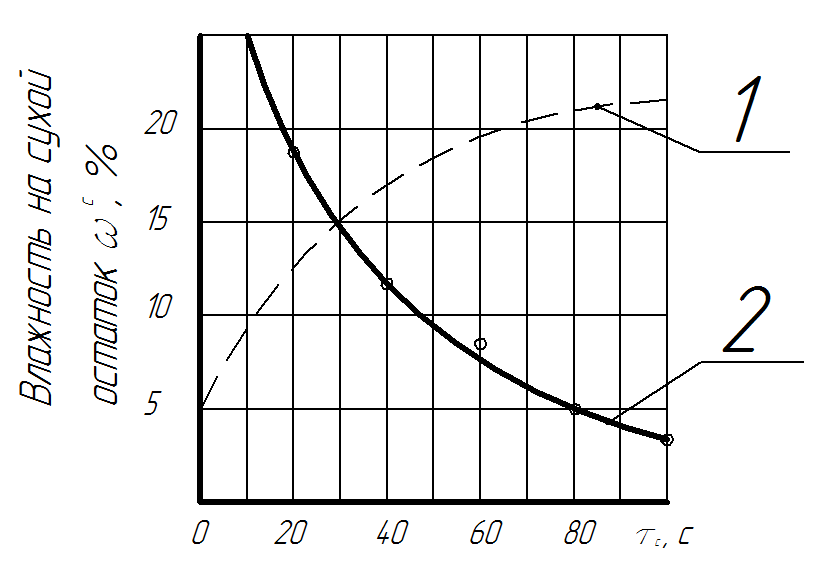
Рисунок 5 – График зависимости ω^c=f(τ_с) –кривая 2 (графическое изображение экспериментальных данных)

Если опытные точки в простых координатах располагаются около монотонных кривых, изображенных на рисунке 5, которые не спрямляются в логарифмических координатах, то можно попытаться спрямить их в полулогарифмических координатах. В этом случае делается предположение, что искомая зависимость описывается уравнениями следующих видов:

для кривой 1 ωc=аеn1τ для кривой 2 ωc=ае-n2τ

(14) (15)

Уравнения вида 14,15 обычно встречается при описании различных тепло-и массообменных процессов, протекающих во времени. Рассматриваемый пример убедительно подтверждает справедливость поговорки: “Природа любит натуральный логарифм”.

Кроме того, подобные монотонные кривые удобно описать зависимостью вида:

У=10а+bх

(16)

Так как

lgy=a+bx

(16а)

то при наличии зависимости данного вида x и lgy связаны линейно, т.е. на полулогарифмической сетке (рисунок 6) зависимость (16а) обращается в линейную.

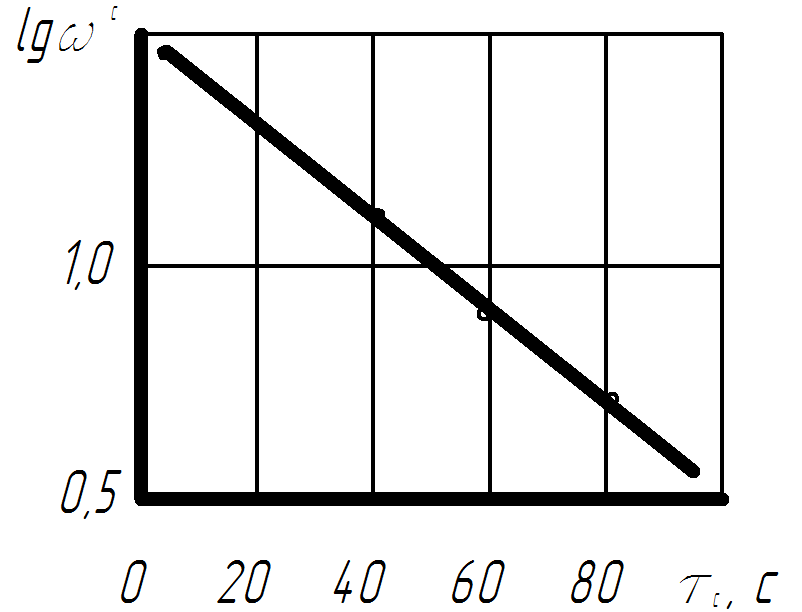
Рисунок 6 – Линеаризованный график уравнения 16 (кривая 2 на рисунке 5)

Полагая у= ω^c, х=τ, найдем эмпирическую зависимость вида(16).

Таблица 4 –

ωc, %	τс, с	lgωc	ωcрасч	Δ, %
29	0	1,4693	28,7	2,7
18,4	20	1,2648	18,6	1,08
11,9	40	1,0755	12,0	0,84
8,0	60	0,9031	7,82	2,50
5,0	80	0,6990	5	0
3,3	100	0,5185	3,3	0

Δ_ср=1,18%

В соответствии с прологарифмированном выражении (16), напишем уравнения

1,4698=a+0·b,

1,2648=а+20·b,

1,0755=а+40·b,

0,9031=а+60·b,

0,6991=а+80·b,

0,5185=а+100·b.

Группируя уравнения по 3 в порядке проведения экспериментов, имеем

3,8101=3·а+60·b,

2,1206=3·а+240·b.

Решая эти уравнения, получим

а=1,4568,

b=-0,00938τ_с.

Подставив полученные значения коэффициентов а и b в уравнение(16), получим следующую эмпирическую формулу

ω^c=10^{1,4568-0,00938τ}