1.5 Рекуррентные формирователи кодовых сигналов

Помехоустойчивость линий связи можно повысить, если в кодовых сигналах за каждым информационным символом будет следовать проверочный. Для формирования проверочных символов используются рекуррентные алгоритмы. Известны два типа рекуррентных формирователей: 1) формирователи систематических кодов; 2) формирователи несистематических кодов.

На рис. 1.5.1 представлена блок-схема формирователя 1-го типа

ПР/ПС – преобразователь параллельных сигналов в последовательные;

ФФ – формирующий фильтр.

Рисунок 1.5.1 – Формирователь систематических кодов

Начальное двоичное сообщение U(k) преобразуется нерекурсивным фильтром и полученный выходной сигнал S₂(k) и сигнал S₁(k) = U(k) – две параллельные последовательности, преобразуются в одну – S(i). Математически этот процесс описывается следующим образом:

(1.5.1)

Так как номер k может быть только целым числом, то последовательность S(i) будет представлять собой ряд

S₁(1) S₂(2) S₁(3) S₂(4) S₁(5) S₂(6) …

Рассмотрим рекуррентный формирователь на основе нерекурсивного фильтра с дискретной передаточной функцией Q(z)=z^-2+z^-4 (кодер Д. В. Хагельбаргера). Его схема представлена на рис. 1.5.2. Сигнал S₂(k) равен U(k-2)S₂(k-4).

Рисунок 1.5.2 – Кодер Д. В. Хагельбергера

Формирователь несистематических кодовых сигналов содержит два нерекурсивных фильтра (рис. 1.5.3)

(1.5.2)

Рисунок 1.5.3 – Формирователь несистематических кодов

Рассмотрим формирователь с двумя нерекурсивными фильтрами

Схема формирователя показана на рис 1.5.4.

Рисунок 1.5.4 – Кодер с двумя формирующими фильтрами

Эффективность кодирования характеризуется кодовым расстоянием. Найдены оптимальные рекуррентные кодеры с формирующими фильтрами:

1. Q₁(k)=111; Q₂(k)=101;

2. Q₁(k)=1111; Q₂(k)=1101;

3. Q₁(k)=11101; Q₂(k)=10011;

4. Q₁(k)=111011; Q₂(k)=110001;

5. Q₁(k)=1111001; Q₂(k)=1011011;

6. Q₁(k)=11111001; Q₂(k)=10100111.

При их использовании минимальное кодовое расстояние будет наибольшим (максимальным)

Повышение помехоустойчивости при рекуррентном формировании кодовых сигналов достигается за счет увеличения длительности сообщения в два раза (или уменьшения в 2 раза скорости передачи информации).

1.6 Схемы и алгоритмы исправления ошибок в разделимых блоковых кодовых сигналах

Блоковые кодовые сигналы сформированы таким образом, что при искажении символов принятый сигнал X(k) не будет делится без остатка на формирующий сигнал Q(k). При делении X(k)=S(k)(k) будет остаток, который можно определить, разделив (k) на Q(k). Рассмотрим семизначный кодовый сигнал, в котором искажен один из семи символов. Перенумеруем их, начиная со старшего разряда: ₁(k)=1000000; ₂(k)=0100000; ₃(k)=0010000; ₄(k)=0001000; ₅(k)=0000100; ₆(k)=0000010; ₇(k)=0000001. Их зет-преобразования равны: ₁(z)=1; ₂(z)=z^-1;₃(z)=z^-2;₄(z)=z^-3;₅(z)=z^-4; ₆(z)=z^-5;₇(z)=z^-6. Если Q(z)=1+z^-2+z^-3 (Q(k)=1011), то можно определить остаток от деления ₁(k) на Q(k):

В результате деления получим: R₁(z)=z^-4+z^-6; R₂(z)=z^-4+z^-5+z^-6; R₃(z)=z^-4+z^-5; R₄(z)=z^-5+z^-6; R₅(z)=z^-4; R₆(z)=z^-5; R₇(z)=z^-6. Таким образом, можно записать коды-опознаватели ошибок: 0000101; 0000111; 0000110; 0000011; 0000100; 0000010; 0000001. На рис. 1.6.1 представлена схема алгоритма формирования оценки сигнала помехи: 1) деление сигнала X(k) на формирующую функцию Q(k) и определения остатка R(k); 2) преобразование остатка R(k) в оценку сигнала помехи ^*(k).

ДО – детектор ошибок

Рис 1.6.1 – Схема формирования оценки помехи и исправления ошибок сигнала

Задача определения остатка решается за 7 тактов (k=1,2,3,4,5,6,7). Этот процесс описывается разностными уравнениями

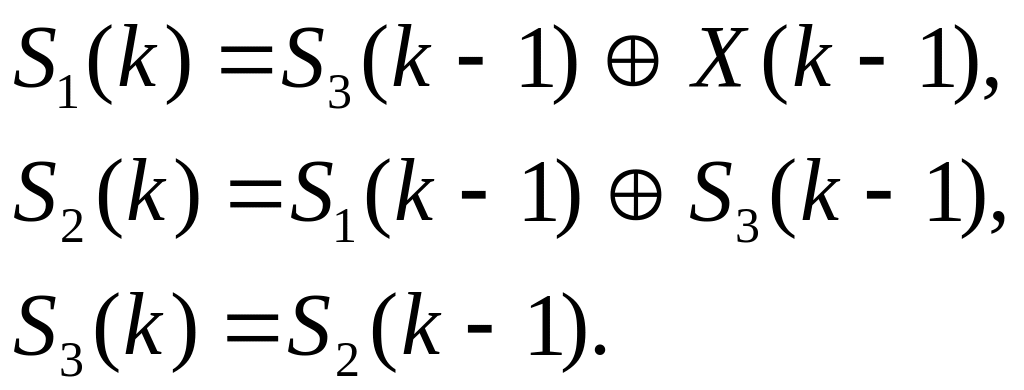(1.6.1)

На восьмом шаге (k=8) ключ принимает положение 1 и определяются D₁(8), D₂(8) и D₃(8):

D₁(8)= S₃(7) X(7), D₁(8) = S₁(7) S₃(7), D₁(8)= S₂(7).

После этого ключ возвращается в положение 2 и S₁(8)=0, S₂(8)=0 и S₃(8)=0.

При k=8,9,10,11,12,13,14 на вход делителя поступает следующая кодовая комбинация, а в схеме преобразования остатка (второй делитель) процесс описывается уравнениями

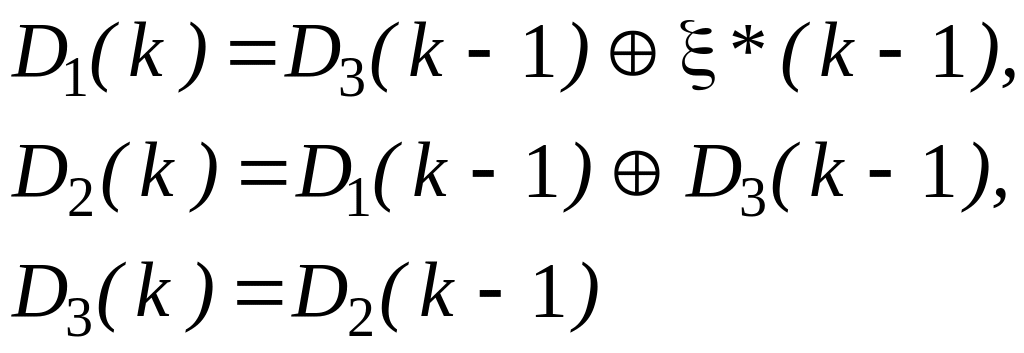(1.6.2)

Рассмотрим формирование оценки помехи, полагая X(k)= (k)=1000000

K	=	1	2	3	4	5	6	7	8
X(k)	=	1	0	0	0	0	0	0	0
S3(k)	=	0	0	0	1	0	1	1	0
S2(k)	=	0	0	1	0	1	1	1	0
S1(k)	=	0	1	0	0	1	0	1	0
K	=	8	9	10	11	12	13	14	15
D3(k)	=	1	0	0	0	0	0	0	0
D2(k)	=	0	0	0	0	0	0	0	0
D1(k)	=	1	0	0	0	0	0	0	0
*(k)	=	1	0	0	0	0	0	0	0

Предположим теперь, что (k)=0001000 и исследуем процесс формирования оценки *(k)

K	=	1	2	3	4	5	6	7	8
X(k)	=	0	0	0	1	0	0	0	0
S3(k)	=	0	0	0	0	0	0	1	0
S2(k)	=	0	0	0	0	0	1	0	0
S1(k)	=	0	0	0	0	1	0	0	0
K	=	8	9	10	11	12	13	14	15
D3(k)	=	0	1	1	1	0	0	0	0
D2(k)	=	1	1	1	0	0	0	0	0
D1(k)	=	1	0	1	1	0	0	0	0
*(k)	=	0	0	0	1	0	0	0	0

Как в первом ((k)=1000000), так и во втором случае ((k)=0001000) ошибка описывается одним и тем же остатком второго делителя: D₃(k)=1; D₂(k)=0; D₁(k)=1. Путем непосредственной проверки легко убедится, что сочетание 101 не зависит от номера разряда искаженного символа. Поэтому детектор ошибки для рассмотренного случая можно описать уравнением

(1.6.3)

Функция – это функция, противоположная функции D₂(k). Например, если D₂(k)=101, то . Операция инвертирования описывается выражением

(1.6.4)

где sgn(x) – функция единичного скачка: sgn(x)=1, если x0, sgn(x)=0, если x<0.

Таким образом, уравнения (1.6.1) и (1.6.2), описывающие процесс определения и исправления ошибки, должны быть дополнены формулами (1.6.3) и (1.6.4). Оценку сигнала получим по формуле

(1.6.5)

Уравнение детектора ошибки зависит от вида формирующей функции Q(k). Например, если Q(k)=1101, то

(1.6.6)

Процесс исправления ошибки в четвертом разряде кодовой комбинации S(k)=10100011 представлен ниже.

K	=	1	2	3	4	5	6	7	8	9	10	11	12	13	114
X(k)	=	1	0	1	1	0	1	1	0	0	0	0	0	0	0
S3(k)	=	0	0	0	1	0	0	0	0	0	0	0	0	0	0
S2(k)	=	0	0	1	0	0	0	0	0	0	0	0	0	0	0
S1(k)	=	0	1	0	1	0	0	1	0	0	0	0	0	0	0
D3(k)	=	0	0	0	0	0	0	0	0	1	1	1	0	0	0
D2(k)	=	0	0	0	0	0	0	0	1	1	1	0	0	0	0
D1(k)	=	0	0	0	0	0	0	0	1	0	1	1	0	0	0
*(k)	=	0	0	0	0	0	0	0	0	0	0	1	0	0	0
X(k-7)	=	0	0	0	0	0	0	0	1	0	1	1	0	1	1
S*(k)	=	0	0	0	0	0	0	0	1	0	1	0	0	1	1