
- •Часть I. Общая теория статистики
- •Тема 1. Предмет и метод статистики
- •Тема 2. Статистическое наблюдение
- •1.Понятие статистического наблюдения
- •Программно-методологические и организационные вопросы статистического наблюдения.
- •Формы, виды наблюдения.
- •Тема 3. Сводка и группировка данных статистического наблюдения Понятие группировки статистических данных
- •Классификация группировок
- •Группировка по количественному признаку
- •Статистические таблицы
- •Тема 4. Статистические величины Абсолютные величины
- •Относительные величины
- •Тема 5. Средние величины Значение средних величин в социально-экономических исследованиях
- •Виды средних величин
- •Тема 6. Статистические ряды распределения и их основные характеристики Вариация признака в совокупности
- •Показатели вариации
- •Нормальный закон распределения
- •Виды дисперсий. Правило сложения дисперсий
- •Тема 7. Выборочное наблюдение Понятие о выборочном наблюдении и его теоретические основы
- •Простая случайная выборка
- •Малая выборка
- •Тема 8. Корреляционно-регрессионный анализ
- •Тема 9. Индексы Понятие индексов
- •Индивидуальные индексы
- •Общие индексы
- •Индексы средних величин
- •Тема 10. Ряды динамики
- •Тема 11. Статистические графики
- •Задания к семинарским занятиям
- •Тема 1.Предмет и метод статистики
- •Тема 2.Статистическое наблюдение
- •Тема 3. Статистическая сводка
- •Тема 4. Статистические величины
- •Тема 5. Средние величины
- •Тема 6. Статистические ряды распеделения и их основные характеристики
- •Тема 7. Выборочное наблюдение
- •Тема 8. Корреляционно-регрессионный анализ
- •Тема 9. Индексы
- •Тема 10. Ряды динамики
- •Тема 11. Графические способы изображения статистических данных
- •Вопросы к экзамену
Показатели вариации
Показатели вариации делятся на две группы:
- абсолютные (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение);
- относительные (коэффициент колеблемости, коэффициент вариации).
1. Наиболее простым является расчет показателя размаха вариации:
h = x max – x min.
Для более точной оценки колеблемости определяют среднее абсолютное и среднее квадратической отклонение. Смысл этих показателей в общем одинаков: они показывают на сколько в среднем отклоняются отдельные значения признака от их средней величины.
Среднее линейное отклонение имеет две разновидности:
- среднее линейное
отклонение простое:
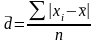 ;
;
- среднее линейное
отклонение взвешенное:
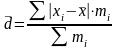 .
.
Этому показателю присущ следующий недостаток – он недостаточно четко реагирует на отклонение вариационного признака. Поэтому в статистической практике наиболее часто для оценки колеблемости используют среднее квадратическое отклонение.
Среднее квадратическое отклонение имеет две разновидности:
- среднее квадратическое простое применяется для несгруппированных данных и имеет вид :
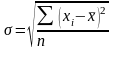 ;
;
- среднее квадратическое взвешенное применяется, если данные сгруппированы и рассчитывается по формуле:
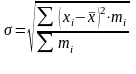 .
.
К относительным показателям вариации относятся:
- коэффициент колеблемости, который рассчитывается следующим образом:
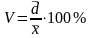 ,
,
где
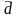 -
среднее абсолютное отклонение;
-
среднее абсолютное отклонение;
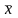 -
среднее значение для х.
-
среднее значение для х.
- коэффициент вариации находится по формуле:

Для характеристики вариационных рядов могут использоваться квартили, квантили и децили.
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3; и остальные 25% превосходят Q3. Квартили определяются по формулам, аналогичным приведенной выше формуле для расчета медианы:
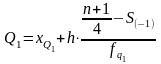 ,
,
где
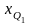 -
нижняя граница интервала, в котором
находится первая квартиль;
-
нижняя граница интервала, в котором
находится первая квартиль;
S(-1) – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль;
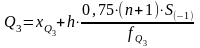 .
.
Условные обозначения те же, что и для величины Q1.
При расчете квантиль совокупность разбивается на 5 частей, децилей – на 10 частей.
Нормальный закон распределения
Укажем особенности кривой нормального распределения.
Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению
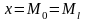 ,
ее величина равна:
,
ее величина равна:
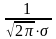
Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значение отклоняется от
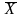 ,
тем реже они встречаются. Одинаковые
по абсолютному значению, но противоположные
по знаку отклонения значения переменной
,
тем реже они встречаются. Одинаковые
по абсолютному значению, но противоположные
по знаку отклонения значения переменной
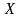 от
равновероятны.
от
равновероятны.Кривая имеет две точки перегиба, находящиеся на расстоянии
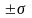 от
.
от
.В промежутке
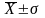 находится 68, 31 всех значений признака.
В промежутке
находится 68, 31 всех значений признака.
В промежутке
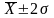 находится 95,4% всех значений признака.
В промежутке
находится 95,4% всех значений признака.
В промежутке
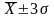
 находится
99,7% всех значений признака.
находится
99,7% всех значений признака.
Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другими.
