
- •Технические средства систем автоматического управления
- •Введение
- •1. Разработка и изготовление средств автоматики
- •1.1. Выбор варианта технологического процесса
- •1.2. Технологичность конструкций блоков систем автоматики
- •Состав показателей технологичности электромеханических устройств сведен в табл. 1.2.6.
- •Коэффициент точности обработки
- •Состав показателей технологичности коммутационных устройств приведен в табл. 1.2.7.
- •Коэффициент повторяемости материалов
- •1.3. Обеспечение точности и надёжности технологических процессов.
- •Допуск размера замыкающего звена
- •Тп состоит из ряда технологических операций, поэтому его надежность оценивается по выражению
- •1.4. Прогнозирование и оптимизация технологических процессов.
- •Поскольку координатами вектора является градиент
- •1.5. Технология производства интегральных схем
- •1.6. Структура технологического оборудования микроэлектроники
- •1.7. Специфика высокочастотных печатных плат
- •1.8. Сборка электронных блоков на пп.
- •1.9. Автоматизированная установка компонентов на пп.
- •1.10. Технология поверхностного монтажа
- •1.11. Электромонтажные соединения в приборостроении
- •Физико-химические основы пайки
- •1.12. Намотка
- •1.13. Пайка групповым инструментом
- •1.14. Подготовительно-заключительные операции групповой пайки
- •1.15. Внутри- и межблочный монтаж
- •1.16. Ультразвук в технологии отмывки электронных блоков
- •1.17. Технология герметизации сау
- •2. Элементы средств автоматики
- •2.1. Параметры, не обладающие свойствами аддитивности
- •2.2. Датчики, области применения, требования.
- •2.3. Емкостные и индуктивные датчики.
- •2.4. Датчики электромашинного типа
- •2.5. Датчики вакуума и силовые датчики.
- •Э. Д. С. Во вторичной обмотке описывается выражением
- •2.6. Устройства сравнения значений параметров
- •2.7. Исполнительные устройства
- •2.8. Элементарные звенья систем автоматического управления
- •3. Структура средст автоматики
- •3.1. Общие характеристики
- •3.2. Структурные схемы сау и правила их преобразования
- •3.3. Автоматическое регулирование
- •3.4. Интегрированные автоматизированные системы управления
- •3.5. Функции эвм в контуре управления тп
- •4. Сбор и обработка информации
- •4.1. Обработка результатов мониторинга
- •4.2. Моделирование возмущенного движения транспортного средства
- •4.3. Испытания электронной аппаратуры
- •4.4. Оптимизация средств контроля и управления
- •Задача адаптации сао возникает в следующих случаях.
- •4.5. Оценка состояния эргатических систем управления
- •5. Применение средств автоматики
- •5.1. В пирометрии
- •5.2. Для камуфляжа информации
- •5.3. Для экстрагирования
- •5.4. В энергетике
- •5.5. В гальванотехнологии
- •5.6. Для резервирования информации
- •5.7. В массометрии
- •5.8. В навигации
- •5.9. В спорте
- •5.10. Для защиты прав потребителей;
- •5.11. Для оценки экологического состояния водоема
- •5.12. Для оценки работоспособности сердца человека
- •5.13. Для направленной кристаллизации расплава лейкосапфира
- •5.14. Для сейсмического зондирования дна водоёмов
- •5.15. Для акустического каротажа осадочного чехла
- •5.16. В управлении судном с глубоководным оборудованием на буксире
- •5.17. В управлении судном в режиме буксировки сейсмокосы
- •5.18. Для управления ориентацией космического аппарата
- •5.19. Для эргатических систем манипулирования
- •5.20. Для коррекции электроэнергии в искажающих системах
- •Заключение
- •Библиография
5.16. В управлении судном с глубоководным оборудованием на буксире
При производстве глубоководных исследований с помощью буксируемых глубоководных, подводных, аппаратов (ПА) в абиссальных районах океана следует учитывать глубину погружения ПА (до 6·106 м и более), незначительную его относительную скорость (до 3 узлов) по профилю, необходимость стабилизации его расстояния от дна (10÷20 м), влияние глубоководных течений на ПА и кабель-трос (КТ), соединяющий НИС с ПА, их массу и объём, а также влияние ветровых и волновых воздействий на НИС при низкой динамичности последнего, причем последний фактор существенно снижает эффективность руля НИС и его управляемость.
При синтезе алгоритмов управления НИС с ПА на буксире возникает необходимость решения двух основных взаимосвязанных задач: определения отклонения ПА относительно заданной линии профиля в горизонтальной плоскости, удаления ПА от поверхности дна водоема; управления движением НИС с целью формирования оптимальных управляющих воздействий на рули НИС для минимизации отклонений ПА от линии профиля и работой траловой лебёдки для обеспечения заданного удаления ПА от дна.
Движение ПА в горизонтальной плоскости относительно профиля представимо выражением вида
ya(t)=yc(t)+yac(t), |
(5.16.1) |
где yc(t) − отклонение НИС от заданного профиля, а yac(t) − отклонение ПА относительно НИС.
Уравнения движения ПА в вертикальной плоскости достаточно удовлетворительно описывается выражениями вида
(m+mx)(d2xT/dt2)+R(gн, vот) cos gн= =0,5 CxrSMx(vот–dxт/dt)2, |
(5.16.2) |
(m+mz)d2zт/dt2+0,5 СzrSMz(dz/dt)2– –R(gн, vот) sin gн=G–W–P, |
(5.16.3) |
где m − масса ПА, p − плавучесть (плотность) ГА; mx, mz.− составляющие присоединенной массы вытесненной ПА воды по осям OX и OZ; Cx, Cz − коэффициенты сопротивления воды движению ПА по тем же осям; SMx; SMz − площади проекций ПА соответственно в вертикальной и горизонтальной плоскостях; r − плотность воды; vот − скорость НИС относительно воды; W − его водоизмещение; m − масса ПА; gк, gн − угол между путевой скоростью и касательной к КТ в точках его соединения с НИС и ПА соответственно. А так как КТ образует гибкую связь НИС с ГА, то уравнение (5.16.1) следует откорректировать с учетом динамики КТ. Учитывая значительную инерционность системы в целом, уравнения равновесного состояния КТ можно представить в виде
хт/l=c(gк, gн), |
(5.16.4) |
zт/l=b(gк, gн), |
(5.16.5) |
где l=varia − длина КТ, стравленного за борт НИС. Линеаризация уравнений (5.16.1), (5.16.2), (5.16.3) и (5.16.4) приводит к выражениям, описывающим отклонения точек позиционирования и скоростей ПА по горизонтальной (вдоль линии профиля) и вертикальной координатам. Движение ПА в вертикальной плоскости зависит от глубины Dh его погружения и скорости движения vот НИС, что показано на рис. 5.16.1

Рис. 5.16.1
Положение ПА на заданном удалении Dh1 от дна водоема достигается путем формирования управляющих воздействий на траловую лебёдку, изменяя длину стравленного за борт КТ, и описывается выражением вида
dx1/dt=A1X1+B1Dl, |
(5.16.6) |
|
min
|
(5.16.7) |
|
при
 1=А1Х1+В1Dl
и X(0)
= X0,
с которым закон изменения Dl
в функции от Dvx,
Dx,
Dvz
и Dz
принимает вид функционала, Dl=Dl0(Dvx,
Dx,
Dvz,
Dz),
здесь qi
(i=1,
…, 4) и R
– весовые коэффициенты.
1=А1Х1+В1Dl
и X(0)
= X0,
с которым закон изменения Dl
в функции от Dvx,
Dx,
Dvz
и Dz
принимает вид функционала, Dl=Dl0(Dvx,
Dx,
Dvz,
Dz),
здесь qi
(i=1,
…, 4) и R
– весовые коэффициенты.
Оптимум управления, по результатам моделирования, достигается при Dl0=KPX1=–R–1ВтРХ1, где Кр − матрица коэффициентов оптимального регулятора состояния траловой лебёдки, а R − решение уравнения Риккати
Aт1P+PA1–PB1R–1Bт1+Q=0, |
(5.16.8) |
здесь Q − матрица весовых коэффициентов qi Результаты моделирования процесса управления положением ПА относительно дна, рельеф которого с уклоном до 45○ относительно горизонта, приводят к выражению
dx1/dt=(A1–B1Kp)x1+Q1g(t), |
(5.16.9) |
Таким образом, задача алгоритмизации процессов управления ГФК в контуре бокового отклонения ПА от заданной траектории состоит в формировании оптимального управления НИС в поперечном направлении (vy), естественно при сохранении vx=const и Dh1=const, но выражения описывающие поведение КТ и vz ПА, представляются дифференциальными уравнениями в частных производных.
Исследования на возможность упрощения, линеаризации и разностно-дифференциальной аппроксимации исходных уравнений в частных производных подтвердили допустимость, с достаточной для практических целей, использования линейных дифференциальных уравнений, что позволяет перейти от краевой задачи к задаче Коши для системы обыкновенных дифференциальных уравнений порядка (2n–2) с постоянными коэффициентами (при разбиении КТ на (n-1) участков). Тогда решение задачи управления ПА в горизонтальной плоскости принимает вид x=AX(t)/dt+Bvy, где Х − вектор состояния ПА; А − матрица размерности (2n–2)´(2n–2); В − вектор размерности (2n–2). Таким образом, решение задачи управления ПА в горизонтальной плоскости реализуемо по функционалу
J=0,5
|
(5.16.10) |
где Q − матрица весовых коэффициентов размерности (2n–2)´(2n–2), параметры которой выбираются с учетом требований по допустимому отклонению Dy и Dz на отрезке времени Dt. Функционал J ® max при оптимальном управлении U*ºvyc, но U*= – BТKX, где матрица коэффициентов K оптимальных обратных связей системы управления по вектору X, получаемая решением алгебраического матричного уравнения вида
На рис. 5.16.2 приведены кривые зависимости натяжения Т, глубины Δу и расстояния Δх между ПА и судном-буксиром от скорости буксировки при фиксированной длине кабель-троса 6000 м. Натяжение Т в точке крепления к судну (у буксирной лебедки) уменьшается с увеличением скорости до 4 м/с и нарастает при дальнейшем увеличении скорости буксировки. При этом ПА с глубины 6 000 м всплывает до 1000 м, но расстояние между аппаратом и судном увеличивается.
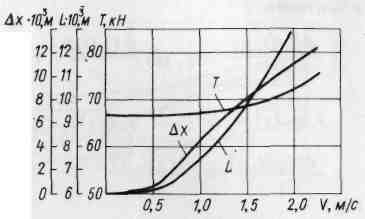

Рис. 5.16.2 Рис. 5.16.3
Здесь показано, как изменяются натяжение Т в точке крепления кабель-троса к судну, длина L кабель-троса и расстояние Δх между ПА и судном с увеличением скорости буксировки при поддержании постоянной глубины погружения ПА на 6000 м. С ростом скорости буксировки до 2 м/с необходимо увеличить длину кабель-троса до 13000 м. Вид статических конфигураций кабель-троса длиной порядка 6000 м в вертикальной плоскости при скоростях буксировки 0,25; 0,5; 1,0 м/с (кривые 1, 2, 3 соответственно) иллюстрируется на рис. 5.16.3.
Особенность движения кабель-троса при буксировке ПА заключается в том, что оно происходит с малыми боковыми и вертикальными скоростями по сравнению со скоростью продольного перемещения кабель-троса. Для любой его точки соблюдаются условия Vz(t, s)<<Vx(t, s); Vy(t, s)<<Vx(t, s); mz(t, s)<<mx(t, s); my(t, s)<<mx(t, s). Ho и скорость поступательного продольного движения практически никогда не превосходит 2 м/с. Кроме того, стремятся, чтобы буксировка протекала плавно, без резких силовых воздействий на кабель-трос.
При этих условиях допускается раздельный анализ динамики движения кабель-троса в вертикальной (продольное движение) и горизонтальной (боковое движение) плоскостях. Уравнения продольного движения записываются в виде
дVx(t, s)/дt= =q1(s) дVx(t, s)/дs+q2(s) дmx(t, s)/дs+q3(s)mx(t, s)+q4(s)Vrx(t, s); |
|
|||
дVy(t, s)/дt= =q1(s) дVy(t, s)/дs+q2(s) дmy(t, s)/дs+q3(s)my(t, s)–q4(s)Vry(t, s); |
|
|
||
дmx(t, s)/дt=дVx(t, s)/дs; дmy(t, s)/дt=дmy(t, s)/дs, |
(5.16.11) |
|||
а бокового
дVz(t, s)/дt= =q1(s) дVz(t, s)/дs+q2(s) дmz(t, s)/дs+q3(s)mz(t, s)–q4(s)Vrz(t, s); |
|
|
дmz(t, s)/дt=дVz(t, s)/дs, |
(5.16.12) |
|
где
q1(s)=2M Vrm0/(m + M); q2(s)=(T0 – MV2rm0)/(m+M); |
|
q3(s)=(T0/дs+kф0V2rm0)/m –M[(kф0+kr0)Vrm0+ωmy0]/m(m+M); |
|
q4(s)=(kф0+kr0)/(m+M); q5(s)=ω/(m+M). |
|
Все коэффициенты qi(s) рассчитываются при постоянных значениях гидродинамической скорости Vr0, ее касательной составляющей Vrm0 и неизменном во времени натяжении кабель-троса, определяемого выражением вида
T0(s)= |
|
Дифференциальные уравнения (5.16.11) и (5.16.12) в частных производных решаются при начальных mх(0, s); mу(0, s); mz(0, s); Vx (0, s); Vy (0, s); Vz (0, s), а также граничных условиях на нижнем mx(t, L); my(t, L); mz(t, L) и верхнем концах кабель-троса, причем последние играют роль управляющих воздействий и складываются из соответствующих проекций скорости движения судна-буксира и изменения длины кабеля L в результате работы буксирной лебедки:
Vx(t, 0)=Vcx(t)–дL sin θ(t, 0)/дt; |
|
Vy(t, 0)=–дL cos θ(t, 0)/дt; |
|
Vz(t, 0)=Vcz(t) – дL cos θ(t, 0)/дt. |
|
Численное решение уравнений динамики кабель-троса может быть получено методом конечных элементов, который позволяет путем дискретизации пространственного аргумента перейти от краевой задачи в частных производных к задаче Коши и системе обыкновенных дифференциальных уравнений. Ниже приводятся некоторые результаты исследований.
На рис. 5.16.4 приведены кривые изменения продольной и вертикальной скоростей движения ПА относительно их начальных установившихся значений, а также приращения координат Δх и Δу центра масс ПА в результате изменения длины кабель-троса на величину ΔL.

Рис. 5.16.4
Основные параметры движения ПА в вертикальной плоскости демонстрируются на рис. 5.16.5. (Основные параметры движения ПА в плоскости XZ: h – глубина, zТ – удаление ПА от дна, xТ и h-zТ – координаты центра тяжести ПА, R – натяжение кабель-троса в точке О, γк и γн углы между касательной к кабель-тросу и осями x и x1 соответственно).
Уравнение движения ПА в плоскости XZ удовлетворяет условиям
(m+mx)(d2xт/dt2)+R(gн, vот) cosgн=0,5CxrSMx(vот–dxт/dt)2, |
(5.16.13) |
и
(m+mz)d2zт/dt2+0,5СzrSMz(dz/dt)2–R(gн, vот) sin gн=G–W–P, |
(5.16.14) |
где учитываются масса m и плавучесть p ПА, составляющие присоединенной массы mx и mz воды по осям OX и OZ, вязкость Cx и Cz по тем же осям, площади проекций SMx и SMz, плотность r воды, скорость vот и водоизмещение W НИС.

Рис. 5.16.5
А так как кабель-трос (КТ) образует гибкую связь и система крайне инерционна (vот£3 узлов), то уравнения равновесного состояния КТ представимы в виде
хт/l=c(gк, gн), и zт/l=b(gк, gн). |
(5.16.15) |
Положение ПА на заданном удалении Dh от дна обеспечивается при выполнении условия
dx1/dt=A1X1+B1Dl, |
(5.16.16) |
а минимизация колебаний Dh – по функционалу
min
|
(5.16.17) |
Оптимум управления по результатам моделирования процессом управления положением ПА относительно дна, с учетом регулирования состояния траловой лебедки, достигается при выполнении условия Dl0=KPX1=–R–1ВтРХ1, Aт1P+PA1–PB1R–1Bт1+Q = 0, для рельефа дна с углом наклона до 45°, моделирование управлением описывается выражением dx1/dt = (A1–B1Kp)x1+Q1g(t), где учитываются матрица Q1 параметров модели ПА и функция g(t), характеризующая рельеф дна. Движение ПА в плоскости по координате y учитывает отклонение yc(t) НИС относительно профиля и отклонение yac(t) ПА относительно НИС
ya(t)=yc(t)+yac(t). |
(5.16.18) |
Таким образом, задача алгоритмизации процессов управления ГФК в контуре бокового отклонения ПА от заданной траектории реализуема по функционалу
J=0,5 f(XтQX+v)dt, |
(5.16.19) |
где Q – матрица параметров, учитывающих требования на допуск Dy(t) и Dz(t).

 (g1Dvx2+g2Dx2+g3Dv2+g4Dz2+RDl2)dt,
(g1Dvx2+g2Dx2+g3Dv2+g4Dz2+RDl2)dt, (XтQX+v)dt,
(XтQX+v)dt, (my0ω+kr0Vrmo)ds.
(my0ω+kr0Vrmo)ds. (g1Dvx2+g2Dx2+g3Dv2+g4Dz2+RDl2)dt.
(g1Dvx2+g2Dx2+g3Dv2+g4Dz2+RDl2)dt.