3) Методы, базирующиеся на теории течения, в дальнейшем условно называемые методами течения.

Эти методы основаны на непрерывном наблюдении за изменением формы и размеров ячейки делительной сетки, которые рассматриваются как непрерывные функции некоторого параметра, чаще всего времени. Хотя за параметр могут быть приняты и геометрические факторы процесса (например, номер ячейки вдоль линии тока и т.п.).

Текущие значения компонентов скоростей деформации (производных по параметру) определяются в любой стадии процесса в произвольной, но предпочтительным образом выбранной системе координат, и используются как для нахождения текущего положения главных осей деформаций, так и для определения интенсивности скорости деформаций .

Значение степени деформации находится интегрированием по параметру

(3)

Согласно теории пластического течения считается, что главные оси скорости деформации совпадают с главными осями напряжения.

Таким образом, экспериментальные методы отличаются способом обработки результатов искаженной делительной сетки.

Общими для всех методов являются допущения о том, что в пределах объема, ограниченного ячейкой делительной сетки: тело считается изотропным, а деформация однородной.

Полученные характеристики процесса формоизменения являются средними и при относительно небольшом объеме, ограниченном размерами ячейки, могут быть отнесены к центру ячейки и рассматриваться как локальные. Естественно, что точность определения такой локальной характеристики зависит от степени неоднородности деформации и должна увеличиваться с уменьшением размеров ячейки делительной сетки. С другой стороны, точность получаемых результатов зависит также и от точности измерения размеров ячейки, которая падает с уменьшением ее линейных размеров. Во всяком случае, минимальные размеры ячейки делительной сетки должны значительно превышать размеры зерен кристаллического тела, так как в противном случае можно ожидать появление микроанизотропии, когда, очевидно, теряют силу зависимости, установленные для идеальных изотропных тел.

Для демонстрации возможностей Mathcad рассмотрим один из наиболее простых методов обработки координатной сетки – метод Э. Зибеля и приведем основные соотношения метода применительно к изучению процесса плоской деформации.

Исходная квадратная ячейка делительной сетки при однородной деформации превращается в параллелограмм. Вписанная в исходный квадрат окружность превращается в эллипс (рис. 1).

Ф иксируются сопряженные диаметры ( и ), соединяющие точки касания эллипса со сторонами параллелограмма, и угол между ними.

Главные оси эллипса определяются так:

, (4)

. (5)

Угол между большой главной осью эллипса и большим сопряженным диаметром вычисляется по формуле:

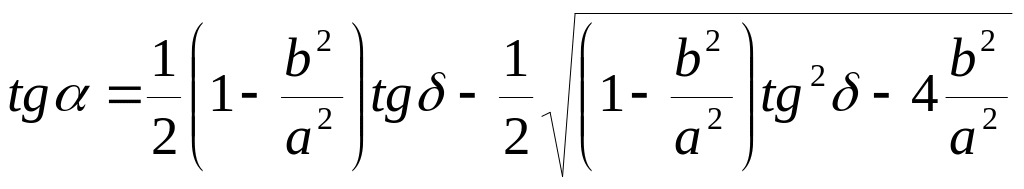. (6)

Главные компоненты деформации находятся по уравнениям:

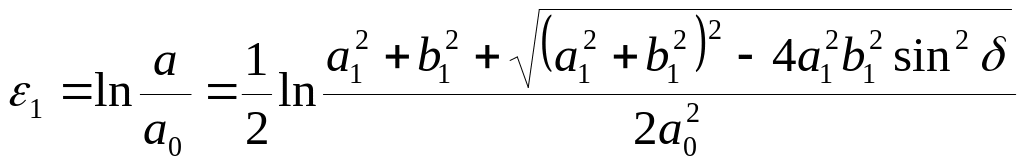; (7)

, (8)

а интенсивность деформации с учетом условия несжимаемости определяется так:

. (9)

Для выполнения расчетов удобно пользоваться координатами точек касания А, В, С и D, а полученные характеристики формоизменения считать локальными для точки О в центре ячейки (рис. 1).