Лабораторная работа № 5 «Цепь переменного синусоидального тока с последовательным соединением катушки и конденсатора. Резонанс напряжений»

Пояснения к работе

Рассмотрим процессы в цепи с последовательным соединением катушки и конденсатора (рис.5.1)

Рис.5.1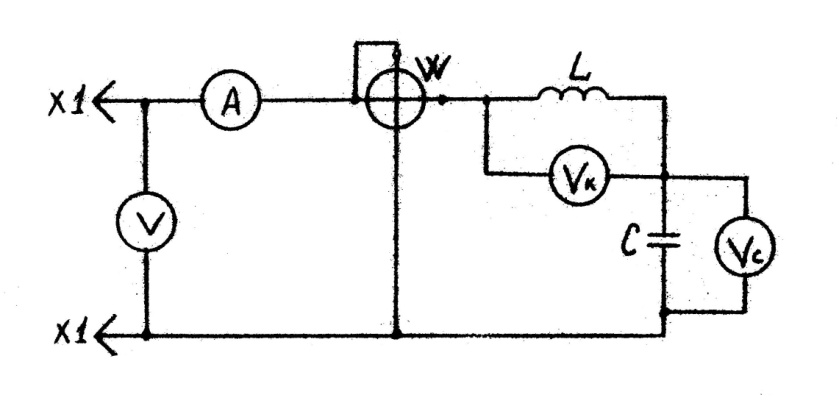

Реальная катушка обладает индуктивным сопротивлением Х_L=ωL

и активным сопротивлением r=ρ , где ω - угловая частота переменного тока, L- индуктивность катушки, ρ- удель­ное электрическое сопротивление провода катушки, - длина про­вода, S - площадь поперечного сечения провода. При прохождении тока через катушку, электрическая энергия расходуется на нагревание провода катушки. Скорость преобразования электричес­кой энергии в тепловую учитывается с помощью величины, называе­мой активной мощностью

P=ri².

Измерив ток и активную мощность катушки можно вычислить активное сопротивление катушки

r=P/I².

Его можно определить также, пропуская через катушку постоянный ток.

В цепи постоянного тока катушка обладает только активным сопротивлением, так как угловая частота ω=2πf=0 и Х_L=ωL=0.

Поэтому r=U/I , где U- постоянное напряжение, приложенное к катушке, а I — сила постоянного тока, протекающего через ка­тушку.

Эквивалентная схема замещения катушки может быть представле­на в виде последовательного соединения резистивного и индуктивного идеальных элементов (рис.5.2).

Рис.5.2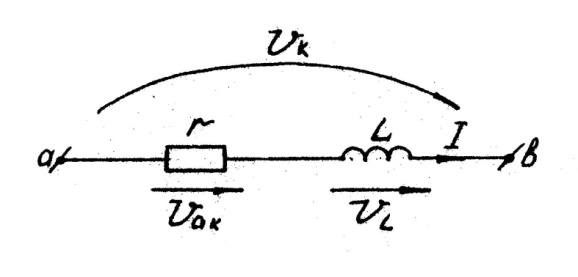

Напряжение на катушке U_k можно разложить на две составляющие - активную U_ak и индуктивную U_L. Векторная диаграмма напряжений и тока для катушки приведена на (рис.5.3).

Рис.5.3

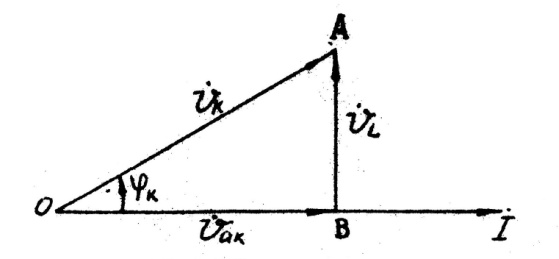
Напряжение U_k можно измерить на выводах катушки с помощью вольтметра,

ток I помощью амперметра. Угол сдвига фаз между током и напряжением катушки φ_к можно определить из формулы P_k= U_kIcosφ_к , если измерить с помощью ваттметра активную мощность катушки P_k .

Составляющие напряжения U_k , U_L и U_ak можно вычислить из треугольника напряжений ОАВ (рис.5.3).

U_ak = U_kcosφ_к или определить графически, опустив перпендикуляр из конца вектора U_k (точка А на рис.5.3) на линию вектора тока I.

Конденсатор в цепи переменного тока обладает емкостным сопро­тивлением X_c = ,

где С - емкость конденсатора.

Следует указать что в конденсаторе также имеются активные потери энергии в диэлектрике. Однако величина этих потерь настолько мала, что ими мож­но пренебречь. На схеме замещения конденсатор можно представить в виде идеального емкостного элемента с параметром С, равным емкости конденсатора.

Последовательное соединение катушки и конденсатора изображе­но в виде схемы замещения на (рис.5.4).

Рис.5.4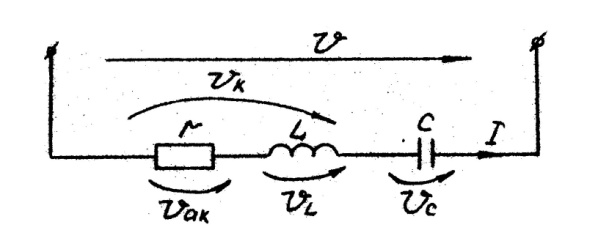

При подключении такой цепи под напряжение U в ней возникает ток I.

Вектор активной составляющей напряжений на катушке Ů_ak будет совпадать по направлению с вектором тока İ (рис.5.5), так как соответствующие синусоиды мгновенных значений совпадают по фазе:

I = I_msinωt и u=ir=I_mrsinωt (5.1)

Рис.5.5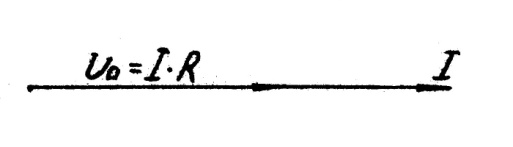

Вектор индуктивного напряжения U_L= İ Х_L опережает по фазе вектор тока İ на 90° (рис.5.6) так как синусоида напряжения U_L индук­тивности опережает по фазе синусоиду тока İ на 90°.

U_L= L = I_m ωtsin(ωt+90^o) (5.2)

Рис.5.6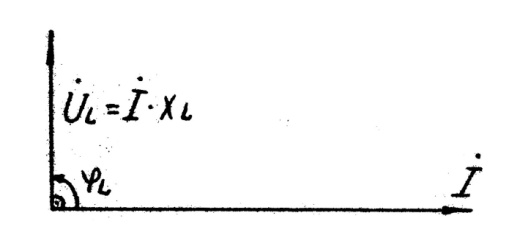

Вектор емкостного напряжения U_с= İ Х_с отстает по фазе от век­тора тока İ на 90° (рис.5.7), так как синусоида напряжения на ем­кости при нулевых начальных условиях отстает от синусоиды тока i на U_c= sin(ωt+90^o) (5.3)

Рис.5.7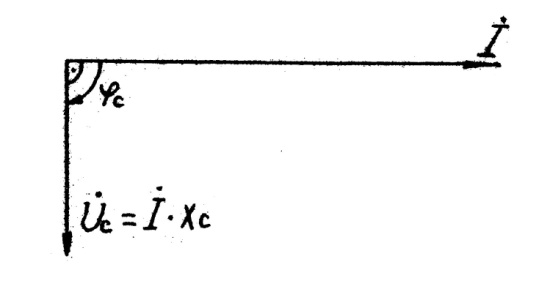

Для рассматриваемой цепи уравнение по второму закону Киргофа имеет следующий вид:

Ů= Ů₀ + Ů_L + Ů_c где Ů₀=IR ; Ů_L= İ Х_L ; Ů_c= İ Х_c (5.4)

Согласно уравнению (4) и рис. 5 - 7, векторная диаграм­ма напряжений цепи (рис.5.4) будет иметь вид, показанный на рис.5.8, где вектор Ů_а совпадает по фазе с вектором İ а вектор Ů_L опережает по фазе на 90° вектор тока İ. Сумма векторов Ů_а и Ů_L дает вектор напряжения катушки: Ů_k= Ů_ak+ Ů_L опережающий по фазе ток на угол φ_к.

Вектор Ů_с отстает по фазе на 90° от вектора тока İ. Сумма векторов Ů_L , Ů_а и Ů_с дает вектор напряжения сети Ů, опережающий ток по фазе на угол φ_к.

Разделив и умножив стороны треугольника (рис.8) на вели­чину İ получим подобные треугольники сопротивлений и мощностей (рис.5.9 -5.10).

Рис.5.8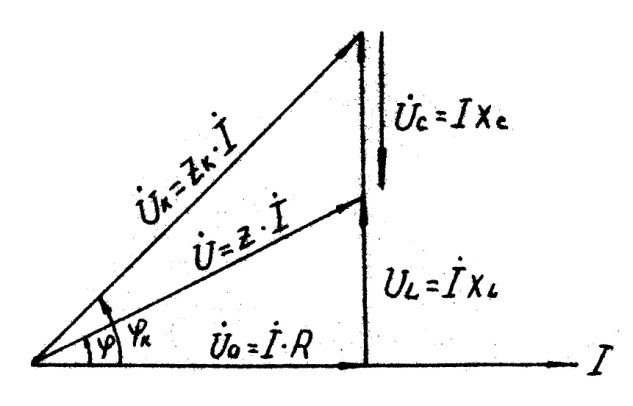

Рис.5.9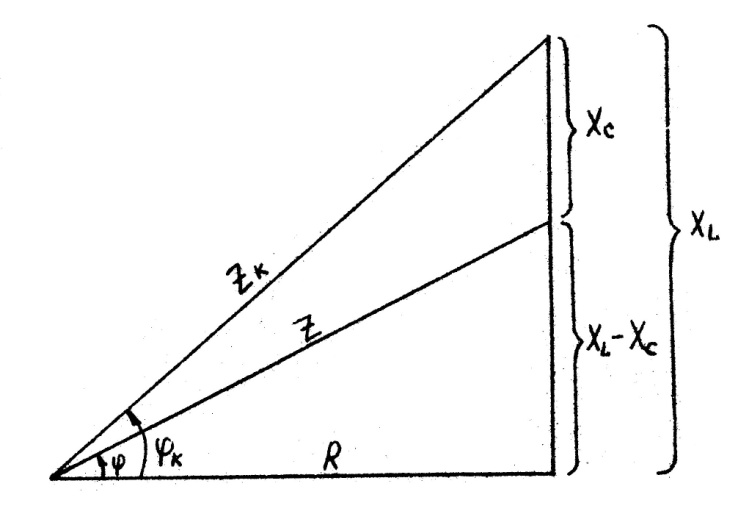

Рис.5.10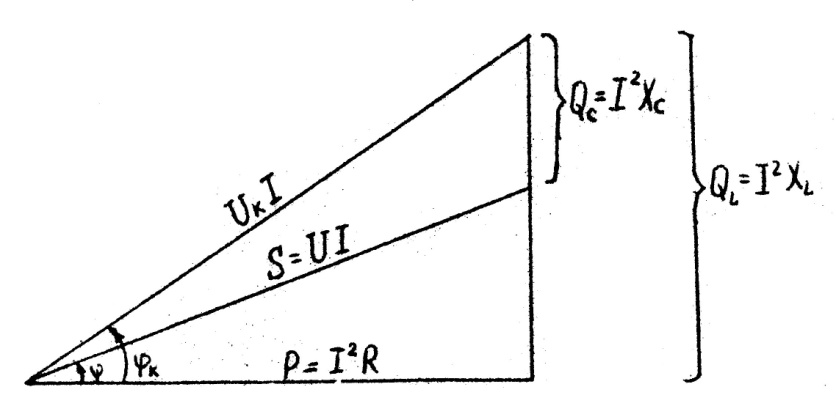

Из треугольника сопротивлений (рис.5.9) найдем полное сопротивление Z и cosφ цепи:

(5.5)

(5.6)

Из векторной диаграммы напряжений (рис.5.8) получим формулу тока I которая является выражением закона Ома для последовательной цепи переменного тока:

(5.7)

Из диаграммы мощностей получим соотношение между полной S, активной P и

реактивными Q_c и Q_L мощностями: (5.8)

Изменяя величину емкости или индуктивности в цепи, можно изменять соотношение между емкостными и индуктивными сопротивления­ми и напряжениями:

U_c= и U_L=I

и получать различные значения угла сдвига фаз φ между вектором тока İ и вектора напряжения сети Ů согласно уравнению (5.6). Если величина имеем: и U_L >U_c в цепи преобладает индуктивное сопротивление X_L и напряжение U_L, поэтому вектор тока İ отстает по фазе от вектора напряжения сети Ů на угол φ (см.рис.5.8).

Если наоборот, преобладает емкостное сопротивление X_c и напряжение U_c, поэтому вектор тока İ опережает по фазе вектор напряжения сети (см.рис.5.11).

Рис.5.11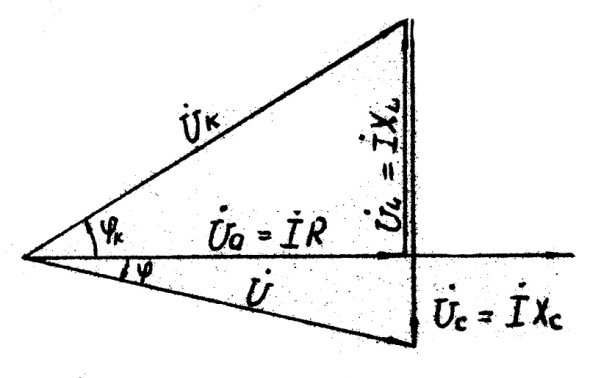

При величине индуктивности L_рез = (5.9)

индуктивное сопротивление будет равно емкостному : (5.10)

следовательно, будут равны между собою индуктивное и емкостное

напряжения (рис.5.12).

IX_L = IX_c ; U_L=U_C (5.11)

Рис.5.12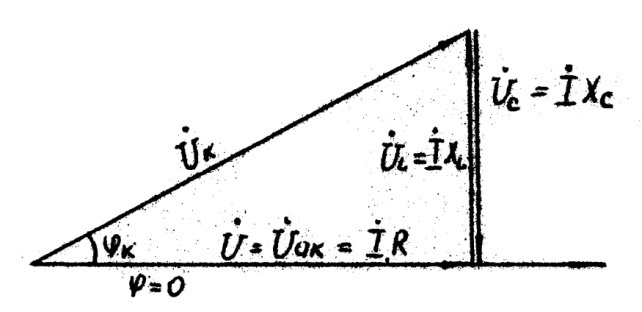

Мы получим резонанс напряжений, т.е. полную взаимную компенсацию индуктивного и емкостного напряжений: Ů_L + Ů_c = 0

При резонансе напряжений угол сдвига фаз φ=0 , следовательно: cosφ =0 (рис.5.12).

Вектор напряжения Ů= Ů_ак (рис.5.12).

Полное сопротивление цепи при резонансе Z_рез принимает минималь­ное значение

Z_рез=r , так как X_L – X_C =0 следовательно, ток при резонансе I_рез и активная мощность принимают максимальные значения:

I_рез =

P=I²_резr=UI_рез (5.13)

Реактивная мощность равна нулю:

Q=I(U_L-U_C)=0 ; Q_L-Q_C=0 (5.14)

Индуктивное U_L и емкостное U_c напряжения в раз больше напряжения сети U:

U_L=U_C= I = X_L= X_C

Поэтому резонанс напряжений может оказаться опасным для установки. При испытании таких цепей требуется особая осторожность. Явление резонанса напряжений, т.е. взаимной компенсации реактивных напряжений (U_L-U_C=0), а, последовательно, и реактивных мощностей (Q_L-Q_C=0) объясняется тем, что мгновенные значения напряжений на индуктивности U_L и на емкости U_c в любой момент времени равны и имеют противоположные знаки. Отсюда следует, что если, например индуктивность берет энергию из сети для создания магнитного поля, то в этот момент конденсатор разряжаясь, отдает энергию в сеть.

Происходит взаимная компенсация энергии потребляемой ими из сети.

Таким образом, при резонансе полная энергия, потребляемая из сети, расходуется только на нагревание резистивного элемента цепи.

Кривые зависимостей полного сопротивления Z цепи от величины емкости С показаны на рис.5.13.

Рис.5.13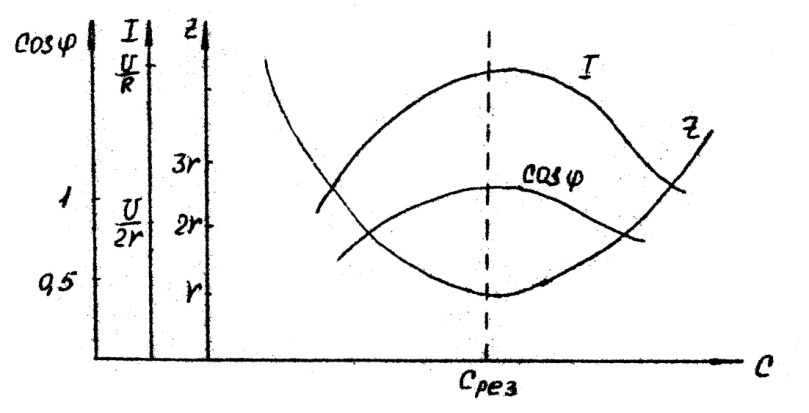

При Ср = величина Z минимальна и равна Z_рез=r.

На рис.5.13 показана также кривая зависимости тока I и cosφ от величины емкости С.

При С = С_рез ток I имеет максимальное значение I_рез = при всех других значениях емкости I= .

Из выражения (5.10) видно что резонанс напряжений в цепи может быть получен изменением индуктивности L или емкости С при неизменной частоте сети f или изменением частоты сети при задан­ных постоянных L и С.