
- •Лабораторная работа № 1 «Поверка амперметра и вольтметра»
- •Порядок выполнения работы.
- •Контрольные вопросы.
- •Лабораторная работа № 2 «Исследование неразветвленной электрической цепи при одном переменном сопротивлении»
- •Лабораторная работа № 3 «Проверка основных законов электрической цепи»
- •Лабораторная работа № 4 «Преобразование треугольника сопротивлений в эквивалентную звезду»
- •Лабораторная работа № 5 «Цепь переменного синусоидального тока с последовательным соединением катушки и конденсатора. Резонанс напряжений»
- •Построение векторных диаграмм
- •Порядок выполнения работы
- •Формулы для вычисления:
- •Контрольные вопросы
- •Лабораторная работа № 6 «Параллельное соединение индуктивности и ёмкости. Резонанс токов»
- •Пояснения к работе
- •Определение параметров всей электрической цепи и её элементов
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 7-8 «Исследование цепи трехфазного тока при симметричной и несимметричной нагрузках фаз. Соединение звездой и треугольником»
Лабораторная работа № 4 «Преобразование треугольника сопротивлений в эквивалентную звезду»
Цель работы: проверить на опыте возможность замены треугольника сопротивлений эквивалентной звездой.
Пояснения к работе
Для упрощения расчета сложной электрической цепи в ряде случаев приходится заменять некоторую часть этой цепи другой, имеющей более удобную схему для дальнейших преобразований. Такая замена должна быть эквивалентной, т.е. не должна отражаться на режиме цепи, не затронутой преобразованием. В ветвях цепи, не вошедших в схему эквивалентного преобразования сохраняются значения токов, мощностей и падений напряжений. К числу таких преобразований относится преобразование соединения треугольника в эквивалентное соединение звездой.
На рис.4.1, а между точками 1,2 и 3 некоторой сложной цепи включены три сопротивления Z12, Z13 и Z23, соединенные треугольником, а на рис. 4.1, б между этими же точками показаны три сопротивления Z1, Z2 и Z3, соединенные звездой.
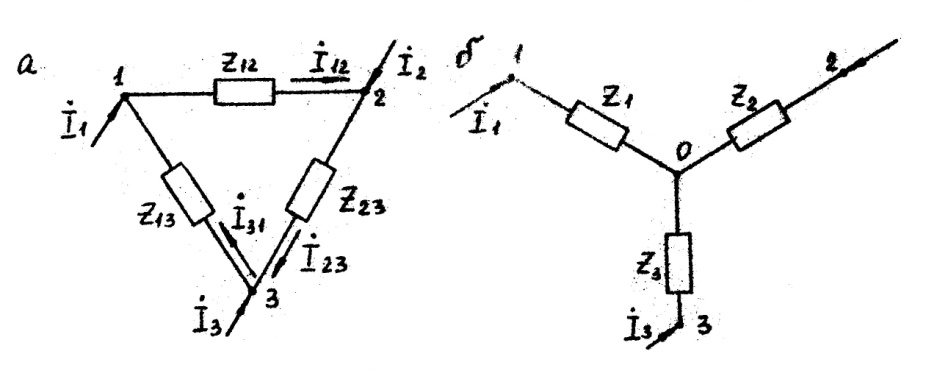
Рис.4.1. Схемы соединений трех сопротивлений; а - треугольником; б – звездой.
Соединения звездой и треугольником эквивалентны друг другу при условии, что при одинаковых в обоих случаях напряжениях Ů12, Ů23, Ů31, между точками 1,2 и 3 токи, подходящие к этим точкам от остальной части цепи одинаковы в обоих случаях.
Составим уравнения по 1-мy и 2-му законам Кирхгофа для схем рис.4.1,а и рис.4,1,6.
Для соединения треугольником



Выражая Ů31 через Ů12 и Ů23 из (4.1) и подставляя это выражение в (4.2) и (4.3) поучим


На основании 2-го закона Кирхгофа для цепи рис.4.1,а справедливо выражение
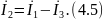
При соединении звездой (рис.4.1,6) уравнения, составленные по законам Кирхгофа, выглядят так

для узла, обозначенного рис.4.1,6 индексом "0".

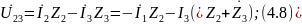
Решая систему уравнений (4.7) - (4.8) относительно токов İ1 и İ3 получим


Где

Поскольку согласно принципу эквивалентности токи İ1 и İ3, а, следовательно, и İ2 в части электрической цепи, не затронутой преобразованием должны остаться одинаковыми при одинаковых в обеих схемах напряжениях Ů12 и Ů23, а следовательно и Ů31, коэффициенты в уравнениях (4.4) и (4.9) так же должны быть одинаковыми для схем звезды и треугольника. Приравнивая эти коэффициенты, получим:


Из этих уравнений отыскиваются сопротивления эквивалентной звезды, если заданы сопротивления треугольника.

Порядок выполнения работы
1. В лабораторной работе изучается схема, показанная на рис. 4.2. Треугольник сопротивлений Z12, Z23, Z31 собирается из реостатов, сопротивления реостатов и значение переменной емкости C
задается преподавателем.
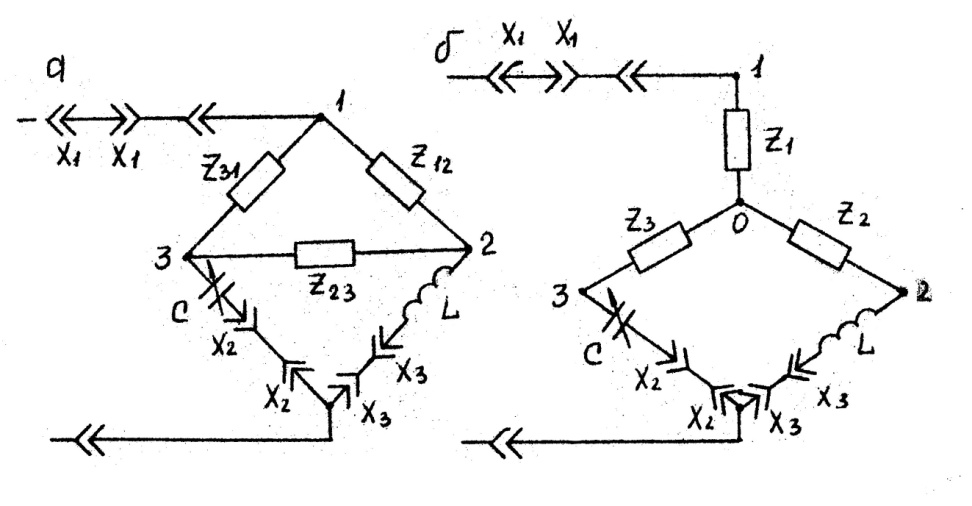
Рис.7.2. Схемы, содержащие треугольник сопротивлений (а) и эквивалентную ему звезду (б)
2. Разъемы X1, X2, XЗ служат для включения амперметра и измерения тока в элементах электрической цепи, не подвергшихся преобразованию.
З. Подобрав необходимые электроизмерительные приборы собрать схему рис.7.2.а, показать её преподавателю, включить и заполнить табл.7.1.
Соединение треугольником
Таблица 4.1.
№ |
U |
U12 |
U31 |
U23 |
UC |
UK |
I |
IC |
IK |
∑P |
1. |
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
4. По данным табл.4.1 рассчитать Z12, Z23, Z31, ZC, ZK и сравнить с заданными или предварительно рассчитанными.
5. Пользуясь формулами (4.11) рассчитать сопротивление эквивалентной звезда, установить на реостатах эти значения и собрать схему рис.4.2.б.
После проверки схемы преподавателем, включить напряжение и заполнить табл.4.2.
Соединение звездой
Таблица 4.2.
№ |
U |
U10 |
U03 |
U02 |
UC |
UK |
I |
IC |
IK |
U12 |
U31 |
U23 |
∑P |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам измерений пользуясь значениями Ů10, Ů03, Ů02 рассчитать напряжения Ů12, Ů23, Ů31 и сравнить с полученными в опыте. Рассчитать сопротивления Z1, Z2, Z3 и сравнить с полученными теоретически.
6. Сравнивая данные табл.4,1 и 4.2 сделать вывода и привести их в отчете.
Контрольные вопросы
1. Пользуясь формулами (4.10) получить сопротивления эквивалентной звезды Z1, Z2, Z3, если известны сопротивления треугольника Z12, Z23, Z31.
2. Записать формулу для эквивалентного сопротивления всей цепи, представленной на рис.4.2.а.
3. Объясните во всех ли случаях возможно преобразование треугольника в эквивалентную звезду.
