Вычисление скорости выхода отцепа из тп

По аналогии (4.4) скорость выхода i+1 отцепа вычисляется:

V_выхi+1 =√ V²_конi+1 +2a _i+1 L_пр , (4.6)

где a _{i +1} <0.

Вопрос возникает в корректности решения уравнения 4.6, где присутствует величина ускорения _i+1 отцепа, который еще не проехал участок пути до координаты прицеливания. Однако всегда можно принять, что ускорение движения _i-го и _i+1 отцепов отличаются некоторым коэффициентом k, т.е. a _i+1 = kа₁.

Тогда выражение (4.6) становится вполне корректным:

V_выхi+1 =√ V²_конi+1 +2k a _iL_пр. (4.7)

Величина коэффициента k отражает различие в динамике движения следующих друг за другом двух отцепов.

Коэффициент k, определяется на том основании, что в соответствии со вторым законом Ньютона, если внешние силы F, действующие на вагоны, одинаковы, то:

т _i a _i = т _i+1 a _i+1.

Отсюда

т_I / т_i+1 = a_i+1/a_i = k (4.8)

Очевидно, что различие в динамике движения может быть определено по относительному соотношению масс движущихся отцепов либо по отношению их ускорений движения в одинаковых условиях. В первом случае коэффициент k определяется на измерительном участке, где определяется весовая категория отцепов. При этом условия движения отцепов должны быть одинаковыми.

Таковым может быть выбрано торможение отцепа замедлителем при одном и том же начальном тормозящем усилии (ступени торможения). Более подробно об этом алгоритме будет сказано ниже, при рассмотрении этапа управления торможением.

Уместно напомнить, что вычисление коэффициента k по отношению масс требует измерения веса вагонов с той же погрешностью, с которой допускается прицельное торможение. Так к примеру, если погрешность скорости соударения допускается ±10 %, то ориентировочно и массы вагонов должны определяться с небольшой погрешностью. Эксплуатируемые весомеры пружинного действия, позволяющие оценивать лишь весовую категорию отцепов для реализации прицельного торможения, мало пригодны.

Различие в динамике движения вагонов для исключения множества влияющих факторов целесообразно определять непосредственно на участках, где производится прицельное торможение.

Алгоритмы прицельного торможения, как известно, предполагают определение координат точки прицеливания, которые вычисляются в виде прогнозных величин L_x. Такие алгоритмы базируются на фильтрации параметров движения отцепа по сортировочному пути с целью определения относительных различий в динамике движения двух следующих друг за другом отцепов. Базовым уравнением, реализованным в системах УУПТ, является следующее:

V_{вых. расч.i} =√ V²_кон +2ka_{сп. i-1}L_{0х i-1},

где L_{0х i-1} – прогнозируемая координата прицеливания очередного i-го отцепа.

Управление торможением отцепов в замедлителях

На рис. 4.19 показаны различные траектории движения отцепов как в режиме торможения на ТП, так и после нее в режиме свободного скатывания.

На ТП происходит быстрое импульсное воздействие тормозящей силы на отцеп, в результате чего резко изменяется динамика его движения вследствие действия инерционных сил. Последствия такого торможения трудно предсказуемы до момента перехода отцепа в режим динамически установившегося движения свободного скатывания и существенно снижают точность прогнозирования движения. Так, кривая 1 характеризует движение отцепа с расчетной скоростью V_вых.р без торможения на ТП в режиме установившегося движения, хорошо описываемого

2

V_вх

3

4

V_вых.р

1 3 2

1,4

V_{кон i}

А L_x1 L_x2

Рис. 4.19. Траектории движения отцепов

уравнением 4.7. Кривые 2, 3, 4 характеризуют разные режимы торможения и, как следствие, различные траектории движения вагонов после торможения. Сле­дует обратить внимание на тот факт, что. в момент оттормаживания замедлителя во всех случаях обеспечивалась одна и та же вы­ходная скорость для одного и того же вагона. Различные траекто­рии движения отцепов после торможения вызваны последствиями действия инерционных сил, о которых было сказано ранее.

Для уменьшения влияния инерционных сил, управление тор­можением отцепов в замедлителях должно быть плавным (мягким), обеспечивающим плавное сопряжение кривых (см. рис. 4.19) в мо­мент оттормаживания. Это обеспечивается при условии равенства величин ускорения в момент оттормаживания отцепа и ускорения свободного скатывания его по участку пути (сортировочному пути). Таким образом, критериями прицельного торможения являются два параметра, определяющие динамику движения отцепов: скорость выхода У_вых и ускорение в момент растормаживания (а = я_св), рав­ное ускорению свободного скатывания отцепа.

На рис. 4.20 показана траектория изменения скорости отцепа, поясняющая реализацию плавного режима торможения (ПРТ). Алгоритм, реализующий его, состоит в следующем.

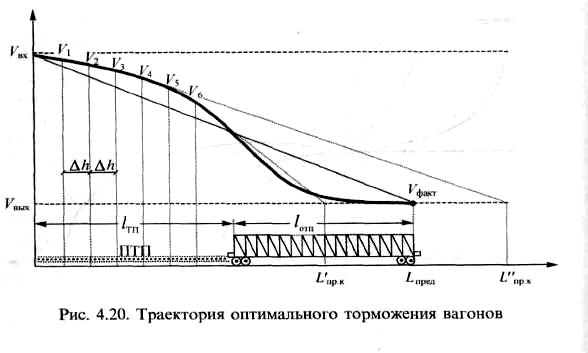
Отцеп въезжает на заторможенный замедлитель, установлен­ный на одну из низших ступеней торможения (I или II). Через рав­ные интервалы пройденного пути ∆h (∆h≠∆l) измеряется скорость движения отцепа:V₁, V₂, ...

По измеренным значениям скорости вычисляются текущие ус­корения a_h и их оценка:

Далее вычисляется на текущей ступени торможения координа­та L_{np к}, в которой скорость станет равной расчетной У_вых;.

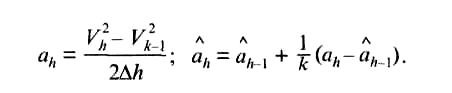
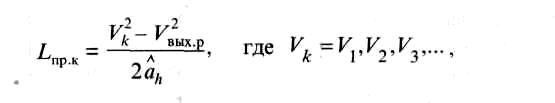
если на текущей ступени торможения окажется, что L _{“np к} > L_{np к},

то необходимо увеличивать тормозящее усилие, т.е. увеличивать ступень торможения. И так до тех пор, пока не будет выполнено неравенство

Минимальная тормозящая сила, обеспечивающая торможе­ние отцепа до расчетной скорости V_BblХ, называется достаточной, а соответствующая ступень торможения—достаточной ступенью тор­можения. На этой ступени продолжается торможение отцепа до достижения им фактической скорости К_факт = К_вых.р в точке L_{пред .} Эта точка, называемая предельной, определяется координатой, в которой должна находиться «голова» отцепа в момент выезда пос­ледней колесной пары его из тормозящих балок замедлителя:

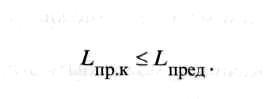
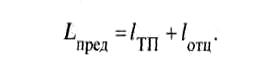
Для вычисления коэффициента к_а достаточно после измерения ускорений а _i = а_{зам i} и а_i+1 = а_замi+1 на начальной, одинаковой сту-

пени торможения, после въезда первой колесной пары отцепа на

замедлитель, определить величину:

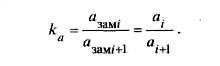
Таким образом, реализация МРТ при заторможенном замед­лителе на одной из низших ступеней торможения позволяет уточ­нить разницу в ходовых свойствах попутно следующих отцепов.

Алгоритм МРТ относится к категории адаптивных алгорит­мов определения реальных ходовых свойств отцепов. При этом, что весьма важно, не требуется априорно определять массы отце­пов. Немаловажно и то, что заторможенное состояние замедлите­ля на низшей ступени торможения практически исключает выдав­ливание отцепов тормозными балками замедлителя и уменьшает время на выполнение команды торможения, связанное с инерци­онностью замедлителя.

Инерционность работы тормозных средств дает предпосылки к появлению погрешностей в реализации скорости выхода F_BbIX отцепа из ТП. Очевидно, как это показано на рис. 4.20, чем плавнее кривая торможения, тем меньше возможная погрешность реали­зации скорости У_вых.

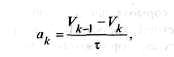
Ускорение торможения а_к может быть вычислено иначе:

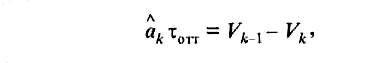где τ — интервал измерения текущих значений скорости, может быть при­нят численно равным т_отг Тогда получим:

положив V_k = Кτ_факт, определяется скорость V_k-1, численно равная скорости, при которой необходимо сформировать команду оттормаживания замедлителя V_0TT:

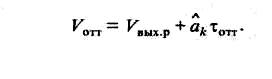
Алгоритм адаптивного управления II ТП, базирующийся на фильтрации параметров движения и статистической экстраполяции, позволяет реализовать МРТ вагонов, повышает эффективность прицельного торможения.

Рассмотренный алгоритм распространяется и на управление торможением отцепов не только на II ТП, но и на один ТП и два ТП.