2.3 Диференціальні рівняння пружної поверхні та внутрішні сили у полярній системі координат
Рівняння Софі-Жермен у полярній системі координат (тільки у випадку симетричного розміщення опор та навантаження) має вигляд
.
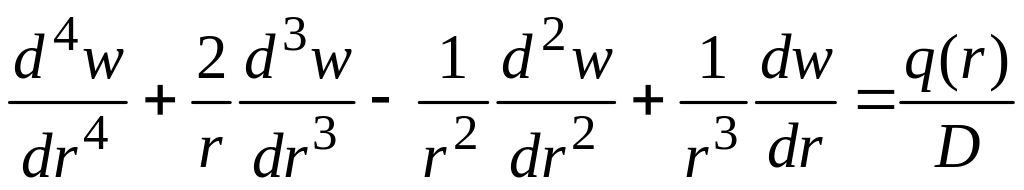Загальний
розв’язок цього рівняння існує при
,
тобто у випадку рівномірно розподіленого
по поверхні пластини навантаження. Він
має вигляд
,
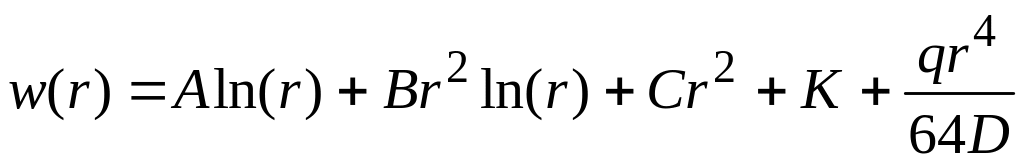де
– константи
інтегрування.
Із загального розв’язку можна визначити:
– кут повороту пластини
;
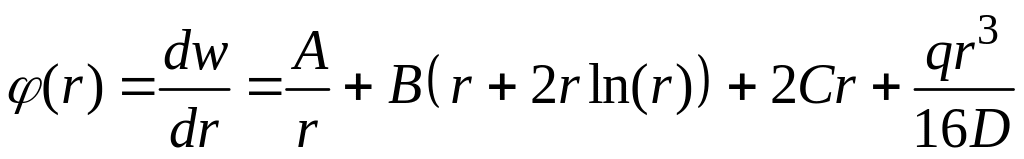– внутрішні сили
;
;
.
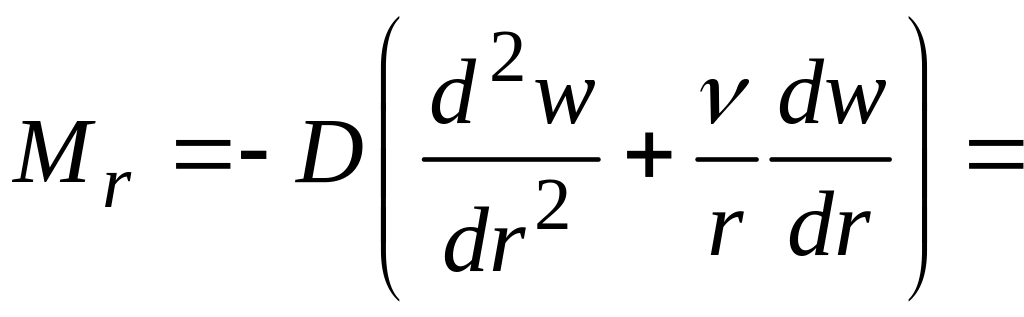
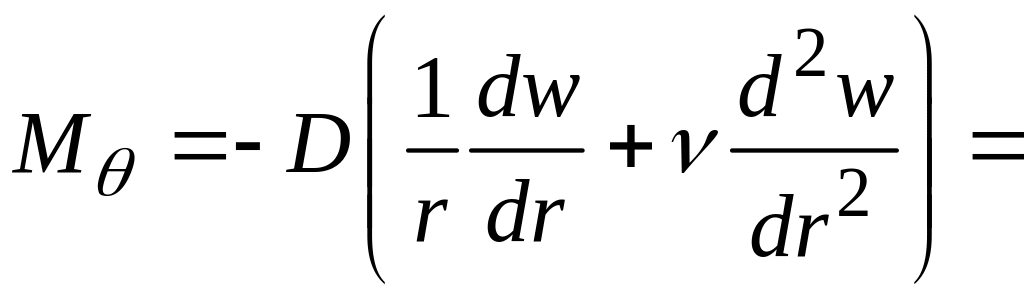
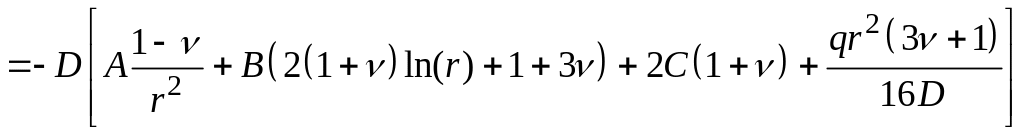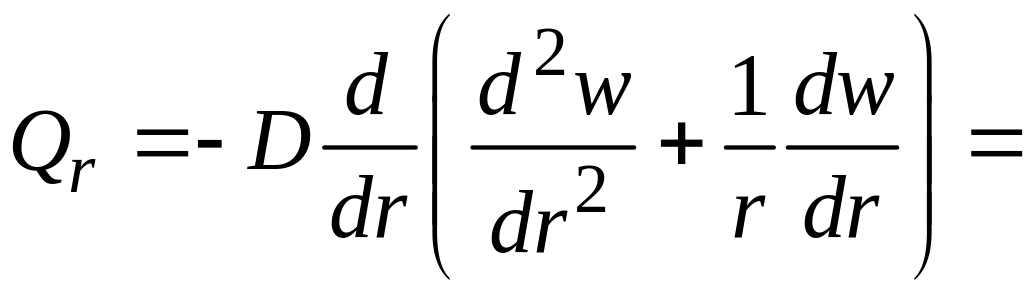
Правила знаків цих внутрішніх сил показані на рис. 2.
Константи інтегрування є сталими для кожної ділянки пластини, де сталою є функція зовнішнього навантаження. Вони у будь-якому випадку можуть бути визначені із кінематичних та статичних крайових умов.
Кінематичними крайовими умовами є:
– умова
скінченності прогинів у центрі для
суцільної (без отвору) пластини. Із
рівняння видно, що при
перший доданок
є скінченним лише при
.
Таким чином, для суцільних пластин
.
Другий доданок
при
є невизначеним, проте
,
тобто константа
може не дорівнювати 0;
– умова рівності нулю прогинів на шарнірній опорі або прогинів та кутів повороту на абсолютно жорсткій опорі;
– умова рівності між собою прогинів та кутів повороту на межі двох сусідніх ділянок пластини.
Статичними крайовими умовами є взаємозв’язки між внутрішніми силами та зовнішніми навантаженнями на границі пластини.
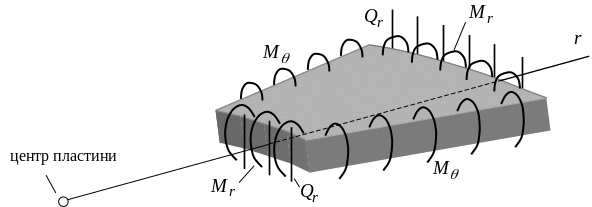
Рисунок 2 – Додатні напрямки внутрішніх сил при згині круглої пластини
2.4 Послідовність виконання роботи та рекомендації щодо її написання
Для прямокутної пластини.
Визначити
умови закріплення (кінематичні крайові
умови) та величину прогину
,
використовуючи задане зовнішнє
навантаження
на поверхню пластини. Показати розподіл
зовнішнього навантаження на контурі
пластини.
Для цього необхідно:
– визначити циліндричну жорсткість пластини;
– перевірити рівність нулю прогинів та кутів повороту на гранях пластини та зобразити схему закріплення;
– шляхом підстановки функції прогинів у рівняння Софі-Жермен визначити константу через інтенсивність розподіленого по площі пластини зовнішнього навантаження ;
– записати рівняння внутрішніх сил та визначити їх розподіл на незатиснених гранях пластини (для шарнірно обпертих – тільки згинальний момент, для рухомого затиснення – тільки поперечну силу) та зобразити їх на схемі.
Для круглої пластини.
Побудувати епюри прогинів та внутрішніх сил для круглої пластини, знайти максимальні напруження.
Для цього необхідно:
– визначити циліндричну жорсткість пластини;
– записати рівняння прогинів пластини , використовуючи загальний розв’язок;
– записати кінематичні та статичні крайові умови, кількість яких обов’язково повинна дорівнювати кількості невідомих сталих інтегрування;
– розв’язати отриману систему алгебраїчних рівнянь;
– використовуючи рівняння – , та отримані константи , записати рівняння прогинів та внутрішніх сил, побудувати їх епюри. При цьому визначити відповідні величини не менш ніж у 5 точках вздовж радіуса пластини;
– визначити максимальні значення внутрішніх сил та напружень.
Варіант індивідуального завдання вибирається із додатків Б та В.