
- •Кафедра автоматизированного электропривода и промышленной электроники
- •Новокузнецк
- •Введение
- •Дифференциальные уравнения и передаточные функции звеньев сау
- •1.1 Задание к разделу 1
- •Линеаризация нелинейных статических характеристик и нелинейных уравнений
- •2.1 Задания к разделу 2
- •Составление и преобразования структурных схем сау
- •Составление структурных схем
- •Преобразование Структурных схем (Алгебра блочных схем)
- •3.3 Задания к разделу 3
- •4 Библиографический список
- •Оглавление
- •654007, Г. Новокузнецк, ул. Кирова, 42
1.1 Задание к разделу 1
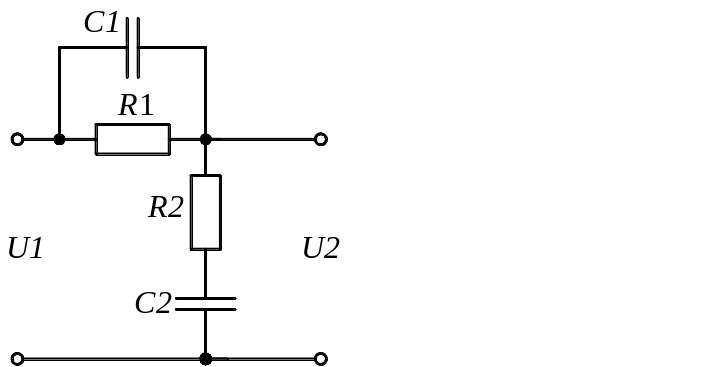
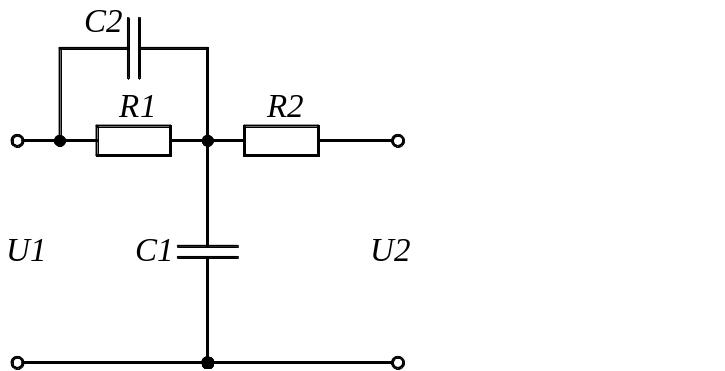
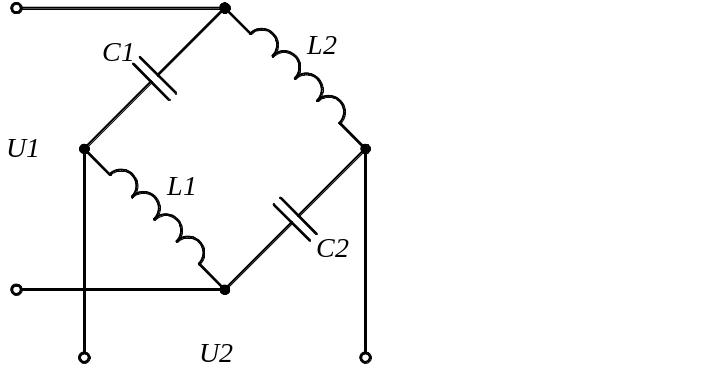
Задание 1.1. Найти дифференциальные уравнения и передаточные функции для представленных на рисунке 4(а-к) схемах.
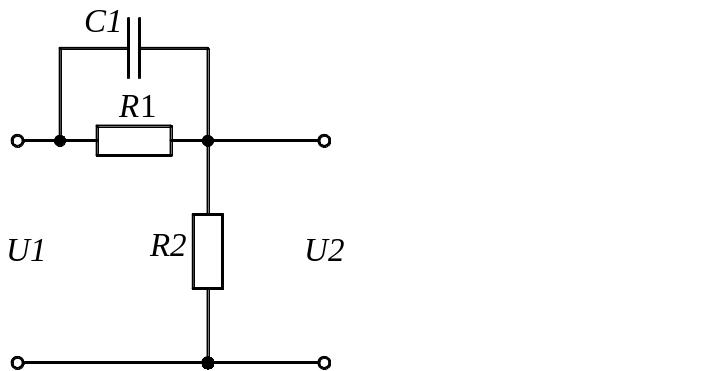
а) б) в)
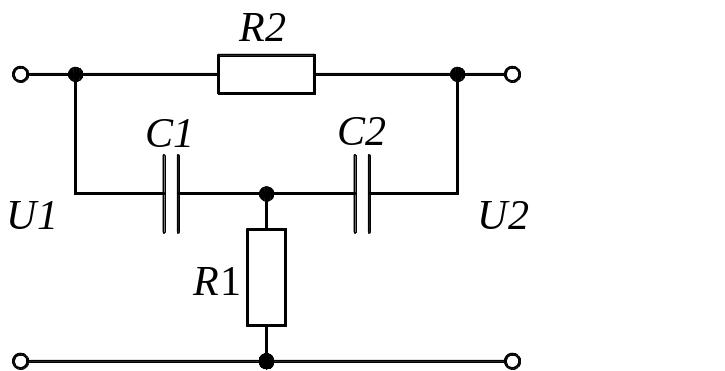
г) д)
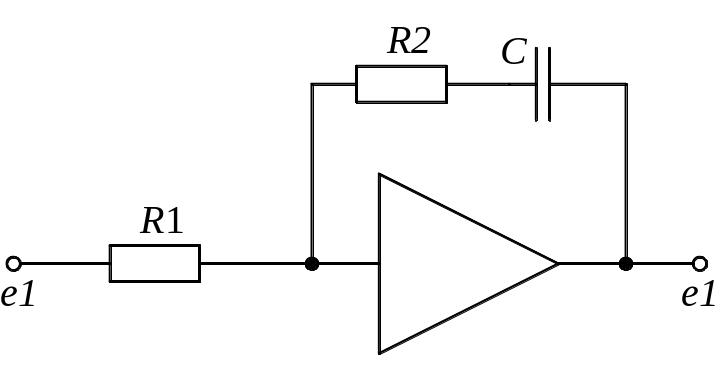
е) ж)
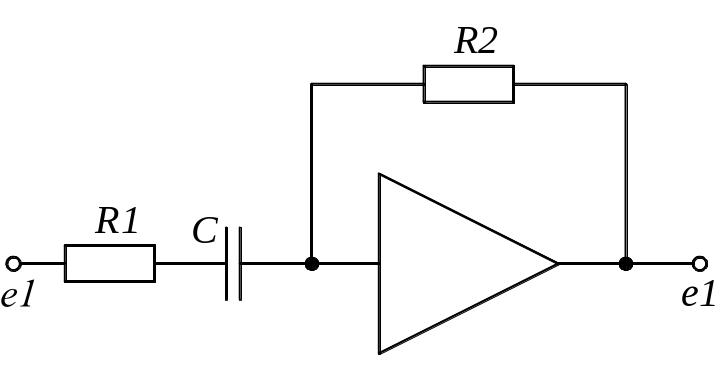
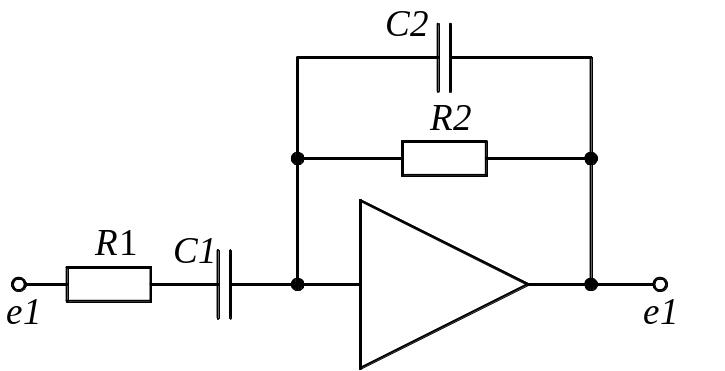
з) и)
 к)
к)
Рисунок 4. Схемы для выполнения задания
Линеаризация нелинейных статических характеристик и нелинейных уравнений
Математическое описание динамики САУ обычно производится путем составления системы дифференциальных уравнений. В общем случае любая реальная динамическая система является нелинейной. Однако большинство непрерывных систем управления могут быть линеаризованы, т.е. заменены приближенно эквивалентными системами, переходные процессы в которых описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами.
Линеаризацией называется замена реальных нелинейных уравнений близкими к ним линейными уравнениями. Линеаризация исходных нелинейных зависимостей основана на методе малых отклонений, сущность которого заключена в том, что динамические свойства звеньев и систем исследуется не во всем диапазоне изменения переменных, а вблизи их некоторых значений, соответствующих характерным режимам работы (например: установившемся режимам). Основой линеаризации является выдвинутое И.А. Вышнеградским предположение, что в течение всего процесса регулирования имеют место лишь достаточно малые отклонения всех измеряющихся параметров от их установившихся значений.
Линеаризация возможна, если:
отклонение переменных малы;
линеаризуемая функция аналитична, т.е. имеет конечные производные всех порядков в окрестности точки линеаризации.
Пусть
задано нелинейное дифференциальное
уравнение звена САУ:
 .
(35)
.
(35)
Уравнение
для установившегося режима
 :
:
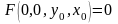 .
(36)
.
(36)
Исходное нелинейное уравнение в отклонениях имеет вид:
 .
(37)
.
(37)
Разложив
левую часть уравнения в ряд Тейлора в
окрестности точки установившегося
режима
 ,
получим:
,
получим:
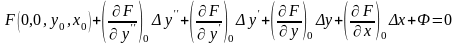 ,
(38)
,
(38)
где
 - частные производные в точки установившегося
режима;
- частные производные в точки установившегося
режима;
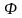 -
члены высшего порядка малости, состоящий
из произведения отклонений, степеней
отклонений с коэффициентами в виде
смешанных частных производных и
производных второго и высших порядков
от F
по соответствующим аргументам.
-
члены высшего порядка малости, состоящий
из произведения отклонений, степеней
отклонений с коэффициентами в виде
смешанных частных производных и
производных второго и высших порядков
от F
по соответствующим аргументам.
Отбросив нелинейный остаток , получим линейное дифференциальное уравнение с постоянными коэффициентами, которые являются результатом линеаризации исходного дифференциального уравнения.
При стандартной форме записи уравнений в ТАУ принято оставлять в левой части выходную величину и её производные, входная величина, её производные и другие величины (возмущения) переносятся в правую часть уравнения:
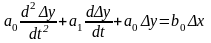 ,
(39)
,
(39)
где
 .
.
Погрешность линеаризации оценивается величиной относительной погрешности:
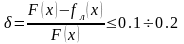 ,
(40)
,
(40)
где
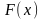 - исходная нелинейная функция;
- исходная нелинейная функция;
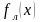 -
уравнение линеаризованной характеристики.
-
уравнение линеаризованной характеристики.
З аметим,
что линеаризация методом касательной
(разложением в ряд Тейлора) дает хорошее
совпадение вблизи точки установившегося
режима и худшее у границ рабочей зоны.
Линеаризация по методу секущей (метод
осреднения) дает хорошее совпадение «в
среднем», хотя наклон секущей не совпадает
с наклоном кривой в рабочей точке
представленной на рисунке 5.
аметим,
что линеаризация методом касательной
(разложением в ряд Тейлора) дает хорошее
совпадение вблизи точки установившегося
режима и худшее у границ рабочей зоны.
Линеаризация по методу секущей (метод
осреднения) дает хорошее совпадение «в
среднем», хотя наклон секущей не совпадает
с наклоном кривой в рабочей точке
представленной на рисунке 5.
а) б)
Рисунок 5. Линеаризация нелинейной характеристики методом касательной (а) и методом секущей (б)
Пример
2.1. В
окрестности точки установившегося
режима
 аналитически
линеаризовать нелинейное уравнение
аналитически
линеаризовать нелинейное уравнение
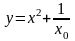 .
.
Решение.
Разложим уравнение
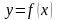 в ряд Тейлора в окрестности точки
установившегося режима:
в ряд Тейлора в окрестности точки
установившегося режима:
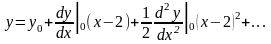 ,
(41)
,
(41)
где
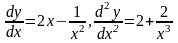 .
.
В точке установившегося режима:
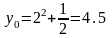 ;
;
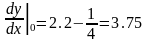 ;
;
 .
.
Таким образом:
 .
(42)
.
(42)
Ограничившись линейными членами разложения получим:
 .
(43)
.
(43)
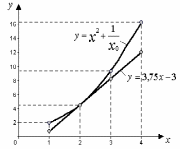
На рисунке 6. приведена линеаризация рассматриваемой нелинейной функции.
X |
1 |
2 |
3 |
4 |
Y |
2 |
4.5 |
9.3 |
16.25 |
X |
1 |
2 |
3 |
4 |
Y |
0.75 |
4.5 |
8.25 |
12 |

Рисунок 6. Линеаризация нелинейного уравнения методом касательной
П ример
2.2.
Вывести дифференциальное уравнение
движения асинхронного двигателя с
короткозамкнутым ротором представленного
на рисунке 7.
ример
2.2.
Вывести дифференциальное уравнение
движения асинхронного двигателя с
короткозамкнутым ротором представленного
на рисунке 7.
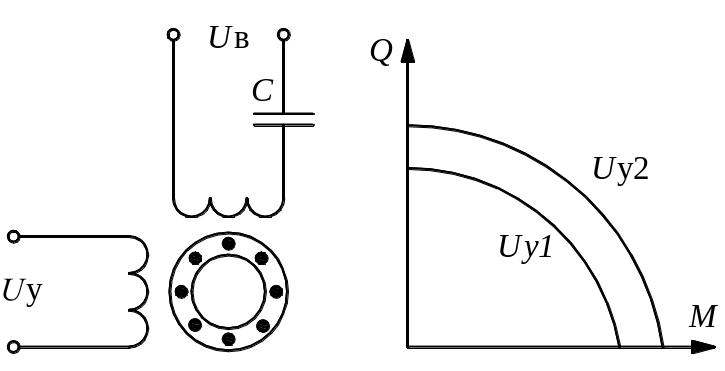
Рисунок 7. Схема включения и механическая характеристика АД с короткозамкнутым ротором
Рабочий механизм с вентиляторной характеристикой:
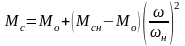 .
(44)
.
(44)
Решение. Основное уравнение движения электропривода:
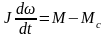 .
(45)
.
(45)
Момент АД:
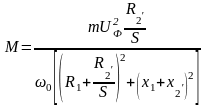 ;
;
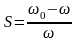 .
(46)
.
(46)
Для
установившегося режима (точка А рисунке
7)
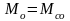
Разлагая
характеристики
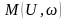 и
и
 в окрестности точки установившегося
режима в ряд Тейлора, получим:
в окрестности точки установившегося
режима в ряд Тейлора, получим:
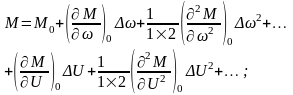 (47)
(47)
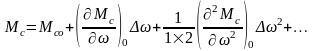 .
(48)
.
(48)
Ограничившись линейными членами разложения, подставим полученные соотношения в основное уравнение движения:
 .
(49)
.
(49)
Поскольку в установившемся режиме , то
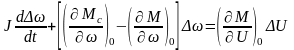 .
(50)
.
(50)
Преобразуем полученное уравнение к виду:
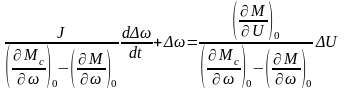 .
(51)
.
(51)
Обозначив:
 ;
(52)
;
(52)
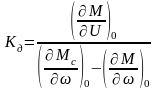 ,
(53)
,
(53)
получим:
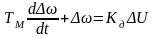 .
(54)
.
(54)
П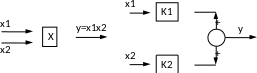 ример
2.3.
Линеаризовать уравнение статической
характеристики множительного устройства,
представленного на рисунке 8,
ример
2.3.
Линеаризовать уравнение статической
характеристики множительного устройства,
представленного на рисунке 8,
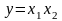 относительно точки установившегося
режима
относительно точки установившегося
режима
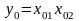 .
.
Рисунок 8. Схема нелинейного и линеаризованного множительного устройства.
Решение.
Рассматриваются небольшие отклонения
переменных
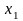 и
и
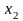 :
:
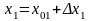 ;
(55)
;
(55)
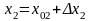 ;
(56)
;
(56)
Тогда:
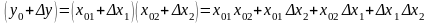 .
(57)
.
(57)
Вычтем из полученного уравнения уравнение установившегося режима:
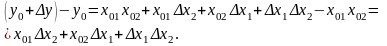 (58)
(58)
Пренебрегая малыми высшего порядка, получим:
 ,
(59)
,
(59)
где
 ,
,
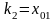 .
.
П

Рисунок 9. Метод осреднения нелинейной статической характеристики.
