1.9 Методы определения констант скоростей и порядков химических реакций

Существуют два основных метода определения констант скоростей и порядков химических реакций: интегральный и дифференциальный.

Интегральный метод. В интегральном методе константа скорости реакции выража­ется через концентрации реагирующих частиц. В случае реакции первого порядка, например, превращения псевдонитролов в нитроловые кислоты

в начальный момент t = 0, [B]_o = 0, [А]_о = а; во время t=τ [В] = х, [А] = а-х.

Тогда выражение для скорости процесса имеет вид

Разделяя переменные и интегрируя, получаем

^.

Отсюда - ln a = c, и в итоге получаем (1.11)

После преобразований уравнения (1.11) получим экспоненциальное выражение для текущей концентрации продукта реакции

Исходя из выражения (1.11) константу скорости реакции можно легко определить гра­фически (рис.1.3). Прямая, приведенная на рис.1.3, называется полулога­риф­ми­чес­кой анаморфозой кинетической кривой. Константа скорости реакции, исходя из выра­же­ния (1.11), может быть определена как тангенс угла наклона прямой 2 на рис. 1.3.

Наряду с константой скорости для характеристики процесса часто используется полупериод реакции. Полупериодом реакции τ_1/2 называется время, за которое половина реагента превращается в продукт реакции. Для реакции первого порядка имеем:

Для реакции второго порядка A+B→C рассматриваем простейший случай, когда [А]_о = [В]_о.

В начальный момент t=0, [А]_о = [В]_о = а, [С]_о=0; во время t=τ [А]=[В]= а—х, [С]=x.

Тогда

Разделяя переменные и интегрируя, получим при условии t=0; x=0:

И сходя из этого выражения, константу скорости реакции второго порядка можно вычис­лить из графика, приведенного на рис. 1.4, как тангенс угла наклона прямой 2. Выражение для расчета полупериода реакции второго порядка имеет вид

.

Рисунок 1.3 - Кинетическая кривая расходования реагента А (1) и ее полу­логарифмическая анаморфоза (2 ) для реакции первого порядка

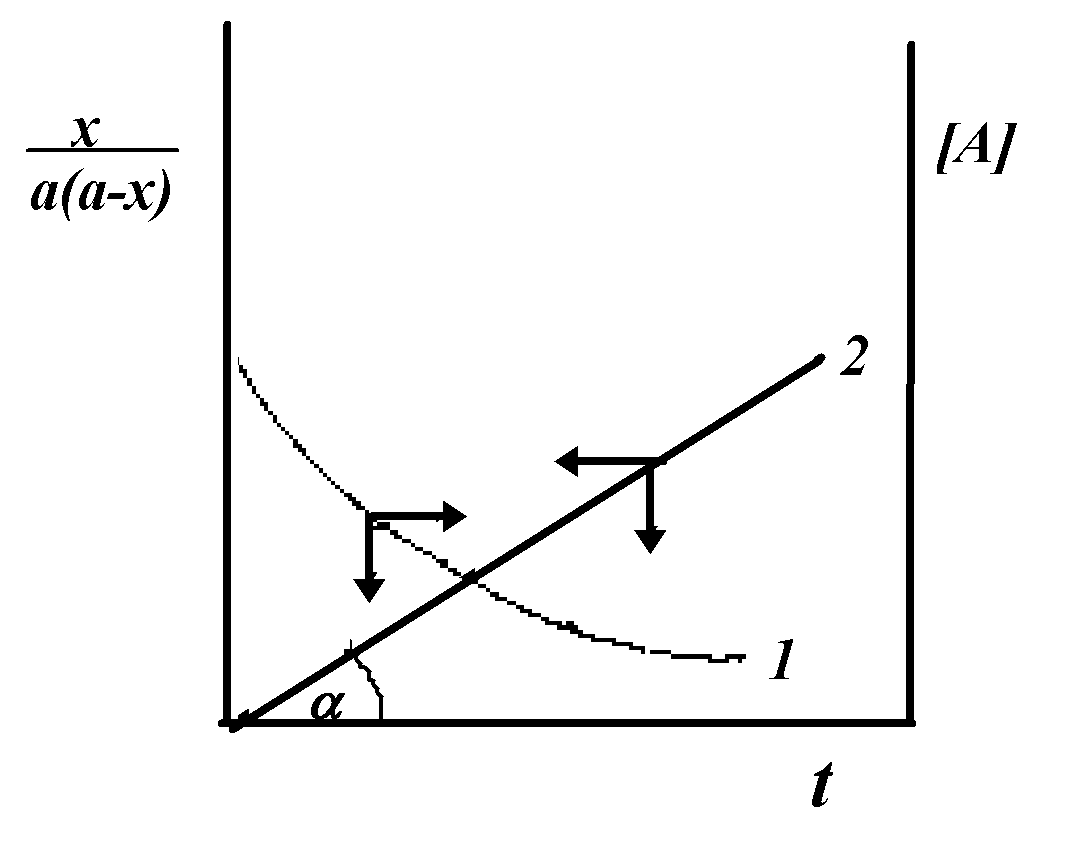
Рисунок 1.4 - Кинетическая кривая (1) )реакции второго порядка и ее анамор­фоза (2)

Дифференциальный метод. Дифференциальный метод определения порядка ско­рос­тей химических реакций был предложен Вант-Гоффом.

Рисунок 1.5 - Графическое определение

порядка и константы скорости реакции

Для реакции n-го порядка уравнение скорости реакции можно записать в виде

Прологарифмировав данное уравнение, получим :

На основании выражения (1.12) можно определить константу скорости и порядок реак­ции графически (рис.1.5). Для этого находят начальную скорость процесса как угловой коэффи­ци­ент касательных к кинетическим кривым при нескольких начальных концентрациях реагента и строят график, аналогичный представленному на рис.1.5. Отрезок, отсекаемый на оси ординат, равен логарифму константы скорости процесса, а тангенс угла наклона прямой к оси абсцисс численно равен порядку реакции.

Рассчитанный таким способом порядок реакции называется концент­рационным, или истинным.

Для расчета порядка реакции можно использовать одну кинетическую кривую, а мгновенные скорости процесса определять как угол наклона касательных к кривой c=f(t) при различных значениях времени реакции t. Далее построение графика в координатах дает прямую линию с угловым коэффициентом , равным порядку реакции (рис.1.5). В отличие от метода начальных скоростей, данный способ расчета позволяет определить т.н. временной порядок реакции, который может отли­чаться от концентрационного в случае сложных реакций, например, если промежу­точные продукты катализи­руют процесс (автокаталитические процессы)

[NO2]*105,моль/л

Рисунок 1.6 - Кинетические кривые распада NO₂ по реакции: 2NO₂→2NO + O₂

1— [NO₂]_o = 18.10^-5 моль/л; 2— [NO₂]_o = 9.10^-5 моль/л

Например, для реакции распада NO₂ по уравнению 2 NO₂→2 NO + O₂ (рис. 1.6) тан-

­генс угла наклона прямой в координатах уравнения (1.12) равен 1,98 (см. рис.1.7), т.е. порядок реак­ции практически равен 2. Используя соотношение (1.12) и метод начальных скоростей, можно получить величину концентрационного, или истинного по­рядка реакции. При определении порядка по методу, представленному на рис.1.7, мы получаем временной порядок реакции.

Рисунок 1.7 - Зависимость скорости распада NO₂ от концентрации NO₂ по ходу реакции, рассчитанная по данным рис. 1.6 (кривая 1)