§6. Смешанное произведение векторов.
Смешанным
произведением
упорядоченной тройки векторов
,
и
называется число
.
Геометрический
смысл
смешанного произведения состоит в том,
что:
,
где
-объём
параллелепипеда, построенного на
векторах
,
и
.
Смешанное произведение обладает свойствами:
1)
;
2)
;
3)
;
4)
и
-компланарны
;
Для
векторов
,
и
,
заданных координатами
,
,
смешанное произведение вычисляется по
формуле:
.
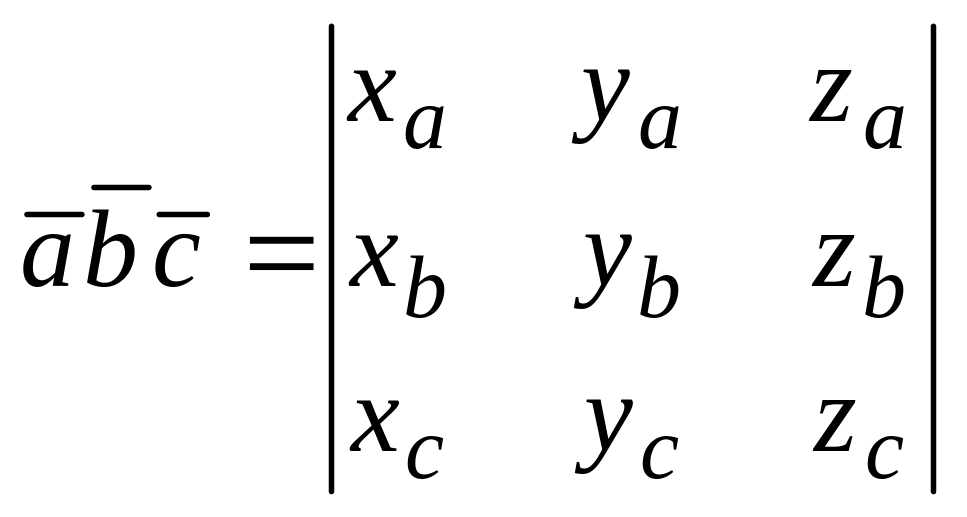Некоторые приложения смешанного произведения:
1)
Вычисление объёмов тетраэдра и
параллелепипеда, построенных на векторах
,
и
,
как на рёбрах:
.
2)
Определение
ориентации упорядоченной тройки векторов
в пространстве: если
,
то тройка правая; если
,
то - левая.
3) Установление компланарности векторов , и :
и
-
компланарны.
4)
Установление
принадлежности четырёх точек
одной плоскости:
2.88
Векторы
образуют правую тройку, взаимно
перпен-дикулярны и
Вычислить
.
2.89
Векторы
образуют левую тройку. Найти
,
если
2.90
Определить
ориентацию тройки векторов
если:
а)
;
б)
.
2.91 Доказать тождества:
а)
б)
2.92
Вычислить произведения, если
:
а)
б)
.
2.93 Проверить, компланарны ли векторы
a)
;
б)
2.94
При каком
векторы
будут компланарны?
а)
б)
2.95
Установить,
образуют ли векторы
базис в множестве всех векторов, если
a)
;
б)
2.96 Проверить лежат ли точки в одной плоскости
а)
,
B(1,2,1),
C(2,3,0),
;
б)
A(7,0,3),
,
,
.
2.97
Вычислить
объём тетраэдра
,
если
,
,
.
2.98
Объем
тетраэдра равен 5, три его вершины
находятся в точках
,
B(3,0,1),
.
Найти координаты четвертой вершины D,
если известно, что она лежит на оси
ординат.
2.99
В тетраэдре
вершины которого расположены в точках
,
,
,
,
найти длину высоты
.
2.100
Вычислить
высоту параллелепипеда, построенного
на векторах
За основание взят параллелограмм,
построенный на векторах
и
2.101
В треугольной
призме
векторы
и
определяют основание, а вектор
направлен по боковому ребру. Найти объем
призмы и ее высоту.
2.102
Даны три
некомпланарных вектора
отложенных
от одной точки О.
Найти длину вектора
где Н -
ортогональная
проекция точки О
на плоскость
АВС.