Выполнение работы

Изменение яркости свечения лампы накаливания осуществляется регулировкой на­пря­жения пи­тания с помощью ручки регулировки на стенде (рис.1). Напряжение нити и ток через нее измеряется вольт­метром и амперметром. Это позволяет подсчитать подводимую мощ­ность .

Рис 1. Передняя панель установки

Яркость свечения нити пирометра регулируется вращением кольца-движка потен­цио­метра, расположенного под окуляром прибора. Сила тока измеряется ампермет­ром пирометра, шкала которого проградуирована в градусах Цельсия. Имеется два диапазона измене­ния температуры: 700 -1400 °C и 1200 - 2000 °С. Для перехода на второй диапазон на пути света от лампы накаливания ставится светофильтр (нажатием и поворотом кнопки, расположенной за шкалой амперметра). С помощью двух выдвижных тубусов (со стороны окуляра и объектива пирометра) обеспечива­ется фокусировка изображения ни­тей.

При достаточно высокой температуре практически вся подводимая мощность рас­сеивается через излучение и пропорциональна энергетической светимости R ~ Tⁿ спи­рали. Поэтому

Р = ВТⁿ,

где В – константа.

Отсюда следует, что

lnP = nlnT + lnB.

Это уравнение прямой в логарифмических координатах.

По результатам измерений постройте график зависимости lnP от и найдите вели­чину n как угловой коэффициент этого графика. Оцените погрешность полученной величины.

Литература

1. Савельев И.В. Курс общей физики. - М.: Астрель, АСТ. 2003 – кн.5, Гл. 1

2. Сивухин Д.В. Общий курс физики. Оптика. - М.: ФИЗМАТЛИТ МФТИ 2002 - Гл. X.

Лабораторная работа № 2 Определение теплоемкости металлов

Цель работы: экспериментальное определение теплоемкости металла, сравнение с законом Дюлонга и Пти.

Теоретическая часть

Теплоемкостью тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус:

.

Удельной теплоемкостью вещества называется теплоемкость единицы массы ве­щества:

Молярной теплоемкостью вещества называется теплоемкость массы вещества, равной молярной массе этого вещества:

, (1)

где m/  количество молей вещества.

Величина теплоемкости зависит от условий нагревания. Процесс нагревания вещества при постоянном объеме характеризуется "теплоемкостью при постоянном объеме" с_{v ,} а при постоянном давлении – "теплоемкостью при постоянном давлении" с_р. Для этих теплоемкостей всегда справедливо соотношение с_p > c_v – это доказывается с помощью термодинамических законов. Например, для идеального одноатомного газа молярные теплоемкости c_v = , а с_р = .

Для твердых тел различие между этими теплоемкостями пренебрежимо мало, так как объем твердых тел при нагревании меняется мало ( при изменении температуры на 1 К). Поэтому говорят просто о теплоемкости твердого тела.

Из теории теплоемкости твердых тел, разработанной Эйнштейном и Дебаем, вытекают следующие важные положения, касающиеся поведения теплоемкости при низких и высоких температурах:

а) при стремлении абсолютной температуры к нулю теплоемкость тела также стремится к нулю

,

б) при температурах, существенно превышающих значение так называемой характеристической температуры Дебая Т_Д, молярная теплоемкость химически простых тел в кристаллическом состоянии есть величина постоянная, и равная

с_ = 3R,

где R = 8,31 Дж/(мольК) – универсальная газовая постоянная.

Последнее утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем и подтверждаемого классической статистической физикой. Действительно, из закона равномерного распределения энергии по степеням свободы следует, что на каждую степень свободы приходится энергии kT/2 (  постоянная Больцмана). В кристаллическом состоянии атомы совершают малые колебания вблизи положения равновесия. На каждую колебательную степень свободы приходится энергия kT, равная сумме средних значений кинетической и потенциальной энергий. Число колебательных степеней свободы из кристалла, содержащего N атомов, равно 3N. Поэтому средняя энергия теплового движения в кристалле равна . Соответствующая молярная теплоемкость равна

,

здесь N_А = 6,0210²³ моль^1 – постоянная Авогадро.

Теплоемкость кристаллов оказывается не зависящей от температуры и от конкретных свойств кристаллов.

Характеристические температуры Дебая некоторых кристаллов приведены в таблице 1.

Таблица 1

Кри­сталл	Pb	J	Na	Ag	NaCl	Cu	Al	Fe	Cr	Be	C (алмаз)
ТД, К	88	106	172	215	281	315	398	453	485	1000	1860

Из приведенной таблицы характеристических температур следует, что для кристал­лов от свинца (Pb) и до поваренной соли (NaCl) комнатная температура (~ 300К) и бо­лее высокие темпе­ратуры являются сравнительно большими. Поэтому для подобных кристаллов отклоне­ния от закона Дюлонга и Пти в этой области температур не велики. Но, например, для бериллия и алмаза поведение теплоемкости при умеренных температурах совершенно отличается от закона Дюлонга и Пти. На рис.1 показана температурная зависимость теплоемкости кристалла меди.

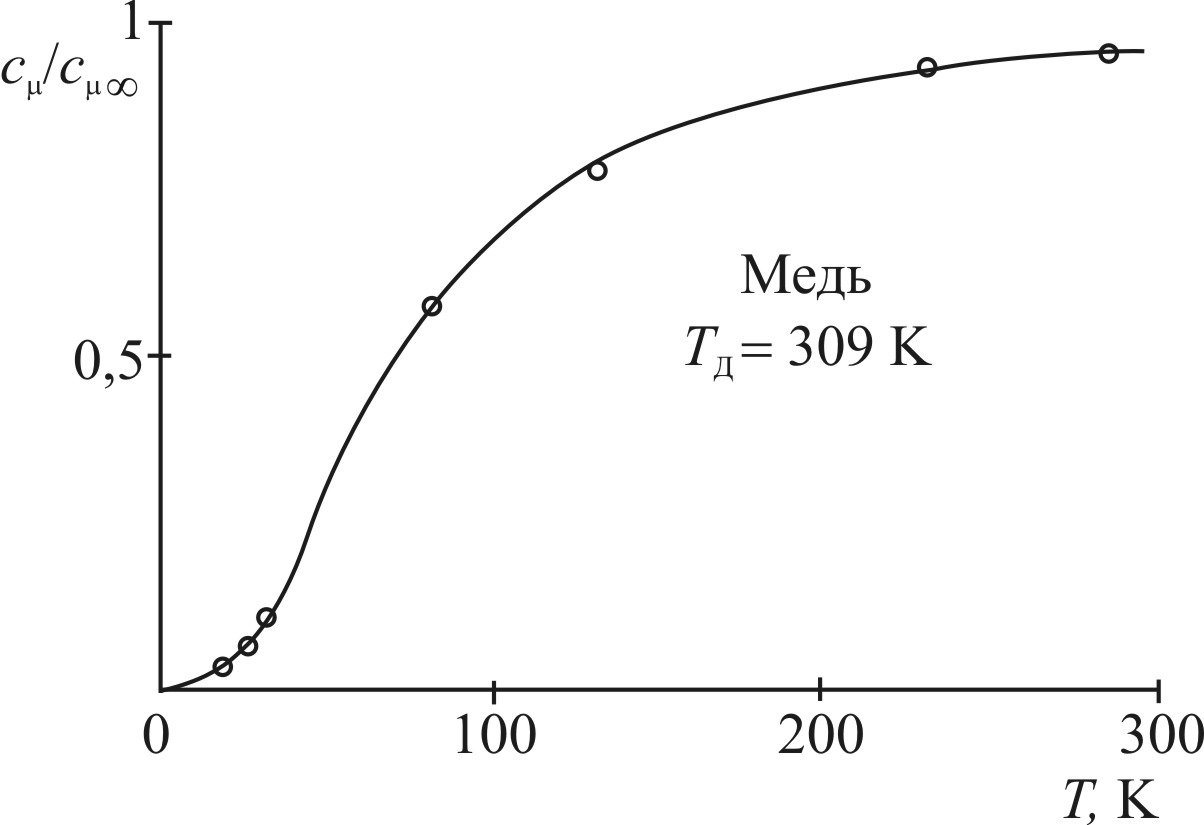
Рис.1 Температурная зависимость теплоемкости меди