4. Связь между площадью сечения и скоростью потока газа. Сопло лаваля

Для установления связи между площадью сечения 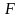и скоростью потока рассмотрим случай горизонтального энер­гетически изолированного течения газа в канале переменного сечения. Воспользуемся уравнением расхода для установившего­ся движения в форме (2.5). Продифференцировав это уравне­ние как произведение трех переменных величин, получим

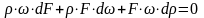
Разделим это уравнение на массовый расход

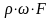
Отсюда находим относительно изменение площади сечения потока

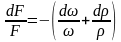(4.1)

Чтобы получить искомую зависимость, необходимо в выражении (4.1) выразить член 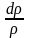через скорость . Для этого воспользуемся уравнением Бернулли (2.22), которое для рассматриваемого случая (потерями давления на гидравли­ческие сопротивления пренебрегаем) примет вид

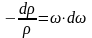
или иначе еще

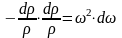
Решая последнее равенство относительно и учитывая определение местной скорости звука и числа Маха, согласно (3.4) и (3.7), имеем

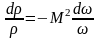
С учетом этого равенства можно представить выражение (4.1) к окончательному виду

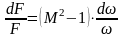(4.2)

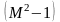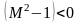которое позволяет провести качественный анализ влияния пло­щади сечения потока на величину его скорости. Выражение , стоящее в правой части равенства (4.3), может принимать как положительное, так и отрицательное значения в зависимости от значения числа Маха. Так, при дозвуковом те­чении газа и, следовательно, . Поэтому, согласно (4.3) и , должны иметь разные знаки. Это равносильно тому, что при дозвуковом течении увеличение площади сечения (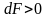 ) ведет к уменьшению скорости по­тока газа (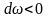 ). И наоборот, уменьшение площади сече­ния ( ) приводит к увеличению скорости газа ( )

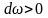При сверхзвуковом течении газа и 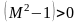. Тогда, согласно (4.3), и имеют одинаковый знак. Следовательно, при сверхзвуковом течении газа увеличение площади сечения потока ( ) приводит к дальнейшему увеличению скорости ( ). И наоборот, уменьшение пло­щади сечения ( ) влечет уменьшение скорости потока газа ( )

Установленное свойство геометрического воздействия на поток газа позволяет спроектировать сопло, которое преобра­зует дозвуковое течение газа в сверхзвуковое, и называется соплом Лаваля (рис. 4.1). Оно состоит из сужающей (дозву­ковой) и расширяющейся (сверхзвуковой) частей. В самом узком сечении сверхзвукового сопла скорость потока должна достигать критического значения, равного скорости звука.

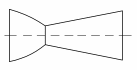
Рис. 4.1 Сопло Лаваля

Сопло Лаваля по форме напоминает трубу Вентури, при­меняемую для измерения расхода маловязкой капельной жидкости. Для избежания отрыва газовой струи конусность расширяющейся части (диффузора) сопла не должна превышать 8-12°.

5. Истечение газа из резервуара через сходящуюся насадку

Рассмотрим установившееся истечение газа из резервуара с большим давлением через сходящуюся насадку (рис 5.1).

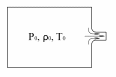
Рис. 5.1. Схема истечения газа из ре­зервуара через сходящуюся насадку

Пусть размеры резервуара достаточно велики, чтобы пре­небречь скоростью газа внутри резервуара, т.е. можно считать, что газ в резервуаре покоится. Обозначим через , площадь выходного сечения насадки, а скорость в давление в этом сечении, соответственно, через 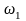и .

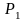Установим зависимость массового расхода газа от внеш­него давления 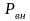, т.е. от давления среды, в которую истекает газ. Забегая вперед, отметим, что возможны случаи, когда давление в выходном сечении насадки равно давле­нию внешней среды и когда отличается от . В дальнейшем этому явлению будет дано физическое объяснение.

Для получения искомой зависимости предположим, что ис­течение происходит настолько быстро, что теплообменом с окружающей средой и трением газа можно пренебречь. Это равно­сильно тому, что процесс изменения состояния газа при исте­чении через насадку - изоэнтропический. Тогда параметры торможения в любом сечении насадки неизменны и соответству­ют параметрам состояния газа в резервуаре , , . Для изоэнтропического процесса, согласно (1.21), можно записать соотношение

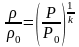(5.1)

Для рассматриваемого течения газа справедливо уравне­ние Бернулли-Сен Венана, которое используем в форм. (2.25) для двух сечений: одно в резервуаре на достаточном удалении от насадки (где скорость движения равна нулю), другое - произвольное сечение в самой насадке.

_(5.2)

Решая это уравнение относительно скорости газа , с учетом соотношения (5.1) получим

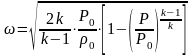(5.3)

Поскольку движение установившееся, массовый расход га­за в любом сечении насадки одинаковый, равный

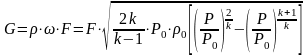(5.4)

Запишем последнее выражение дня сечения на выходе из насадки. Для этого достаточно заменить в нем на и на

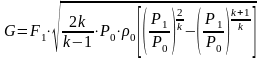(5.5)

Выражение (5.5) и является искомой зависимостью 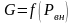. При этом пока (до выяснения физической сущности) будем считать, что 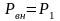. Проанализируем полученное выражение (5.5). В частности, найдем значение , при котором достигает максимального значения.

Для удобства введем обозначение 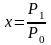. Рассмотрим функцию, заключенную в квадратных скобках выражения (5.5), которая с учетом принятого обозначения имеет вид

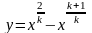(5.6)

Эта функция дважды обращается в нуль: при и при 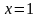, следовательно, в интервале [0,1] она имеет экстре­мум. Для отыскания экстремума необходимо приравнять нулю первую производную

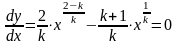
Решая полученное уравнение относительно , получим

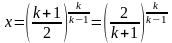(5.7)

следовательно, при значении

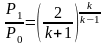(5.8)

массовый расход газа через сходящуюся насадку достигает эк­стремального значения. Можно показать, что это максимум. Сравнивая (5.8) с выражением (3.15), видим, что . Следовательно, массовый расход достигает максимума при .Значение 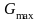может быть найдено либо по формуле (5.5) подстановкой в него , либо по формуле 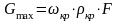. Подставляя сюда значения 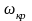и по формулам (3.10) и (3.15), получим окончательно выра­жение

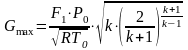(5.9)

Таким образом, согласно формулы (5.5), массовый рас­ход газа через сходящуюся насадку с уменьшением давления (правая ветвь кривой на рис. 5.2) возрастает до тех пор, пока не станет равным критическому , а скорость газа при этом достигнет звуковой, т.е. 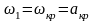. Дальнейшее снижение внешнего давления в соответствии с фор­мулой (5.8) должно приводить к уменьшению массового рас­хода (левая ветвь ОА кривой на рис. 5.2, показанная пунк­тиром). Однако опыт показывает, что при изменении внешнего давления в диапазоне массовый расход газа через сходящуюся насадку остается постоянным, равным максимальному значению, определяемому формулой (5.9). При этом давление газовой струи на выходе из насадки остается неизменным, равным , т.е. между и возникает разрыв. Такому явлению можно дать следующее физическое тол­кование.

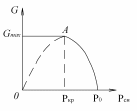
Рис. 5.2 Зависимость массового расхода rasa от внеш­него давления (среды) при истечении через сходящуюся насадку

Пунктирная ветвь кривой на рис. 5.2 может быть реали­зована только при сверхзвуковом течении. Получить такое те­чение с помощью сходящейся насадки невозможно. Для перехода к сверхзвуковым скоростям необходимы специальные условия, а именно, чтобы площадь сечения газового потока после достиже­ния звуковой скорости увеличивалась (см. свойства сверх­звуковых и дозвуковых потоков). Поэтому выражение (5.5) для массового расхода газа при истечении через сходящуюся насадку имеет физический смысл только при 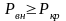(область дозвукового течения). Именно в этой области выполняется равенство 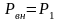. При скорости газа в конце насадки, равной скорости звука, изменение возмущений (давления) во внешней среде не может проникнуть через насадку, так как оно будет сносится струей газа со скоростью звука (с такой же скоростью распространяются и малые возмущения). Созда­ется барьер, который и объясняет наличие скачка давлений (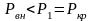 ) при звуковой скорости истечения газа.

Параметры потока изменяются: давление, температура, плотность и скорость газа, изменяются вдоль насадки. Для изменения давления можно получить выражение, если прирав­нять массовые расходы по формулам (5.4) и (5.5)

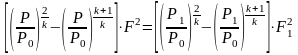(5.10)

И зменение давления газа при истечения через сходящуюся насадку со звуковой скоростью для случая 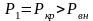можно представить графически (рис. 5.3)

Рис. 5.3. Изменение давления в потоке газа при исте­чении через сходящую­ся насадку

Из рис. 5.3 видно, что вдоль сходящейся насадки давле­ние плавно снижается до значения (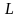 - длина насадки). На выходе из насадки давление в газе претерпевает скачок до