Е. И. Степановских, л. А. Брусницына, т. А. Алексеева физическая химия Примеры решения задач

УДК 544(076)

Составители: Е. И. Степановских, Л. А. Брусницына, Т. А. Алексеева

Научный редактор доц., канд. хим. наук В. И. Двойнин

Физическая химия. Примеры решения задач : методические указания по курсу физической химии. В 2 ч. Ч.1 / сост. Е. И. Степановских, Л. А. Брусницына, Т. А. Алексеева. Екатеринбург : УрФУ, 2012. 71 с.

Методические указания являются дополнением к имеющимся учебникам и предназначены для самостоятельной работы над курсом физической химии.

Библиогр.: 3 назв. Табл. 9. Рис. 12. Прил. 3.

Подготовлено кафедрой физической и коллоидной химии

© Уральский федеральный

университет, 2012

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ПОНЯТИЯ

 Давление (p). Единицы измерения [p] = атм; бар; Па.

1 атм = 1,01310⁵ Па. 1 бар = 1,010⁵ Па.

 Объем (V). [V] = л; м³; см³.

1 л = 1000 мл = 10³ см³ = 10^3 м³ ; 1 см³ = 110^6 м³.

 Температура (Т) в шкале Кельвина. [T] = К.

 Температура (t) в шкале Цельсия. [t] = ^оС.

1 К = 273,15 + ^оС

 Масса (m). [m] = кг; г. 1 кг = 1000 г.

 Число молей (n ). [n] = моль.

 Теплоемкость системы (С ). [C] = Дж/К.

 Изобарная теплоемкость системы ( ). [C_p] = Дж/К.

 Изохорная теплоемкость системы (C_v). [C_v] = Дж/К.

 Мольная изобарная теплоемкость системы ( ).

[ ] = Дж/(Кмоль).

 Мольная изохорная теплоемкость системы ( ).

[ ] = Дж/(Кмоль).

 Удельный объем чистого вещества ( ). [ ] = м³/кг.

 Мольный объем чистого вещества ( ). [ ] = м³/моль.

 Плотность массы чистого вещества (ρ^о). [ ^о] = кг/м³ .

 Работа (A). [A] = Дж.

 Количество теплоты ( Q). [Q] = Дж.

 Энтропия (полная, всей системы) (S). [S] = Дж/К.

 Мольная энтропия (s). [s] = Дж/(мольК) .

 Внутренняя энергия (U). [U] = Дж.

 Мольная внутренняя энергия (u). [u] = Дж/моль.

 Энтальпия (полная, всей системы) (Н). [H] = Дж.

 Мольная энтальпия (h). [h] = Дж/моль.

 Энергия Гиббса (G). [G] = Дж .

 Мольная энергия Гиббса (g). [g] = Дж/моль.

 Мольная доля компонента k (N_k).

 Массовая доля компонента k (φ_k).

 Мольный объем ( ). [ ] = м³/моль.

 Удельный объем ( _уд). [ _уд] = м³/кг.

 Парциальный мольный объем компонента k ( ).

[ ] = м³/моль.

 Глубина химической реакции (кси)( ).

 Стехиометрическое число компонента k в реакции ( ).

 Стандартная мольная энтальпия реакции ( ).

 Стандартная мольная энтальпия образования вещества k

( ).

 Стандартная мольная энтропия реакции ( ).

 Стандартная мольная энтропия вещества k ( ).

 Стандартная мольная изобарная теплоемкость реакции r

( ).

 Константа равновесия реакции r в pшкале ( ).

 Уравнение состояния идеального газа  системы невзаимодействующих частиц точечного размера;

, (А)

где n  количество вещества (в молях);

R  универсальная газовая постоянная,

R = 8,314 Дж/(мольК) = 1,987 кал/(мольК) = 0,0821 латм/(мольК).

 Нормальные условия  это температура 0 ^оС и давление 1 атм.

 Первый закон (первое начало) термодинамики:

энергия изолированной системы постоянна −

.

В неизолированной системе энергия может изменяться за счет:

а) совершения системой работы над окружающей средой;

б) теплообмена системы с окружающей средой.

Математическая формулировка первого закона для закрытых систем:

dU = Q  A ; U = Q  A. (Б)

Буквы  в уравнении (Б) отражают тот факт, что Q и A не являются функциями состояния, они служат формами передачи энергии и связаны с процессами, а не с состояниями системы. Их называют также функциями перехода и бесконечно малое изменение теплоты и работы не является полным дифференциалом.

Теплота может переходить в систему при нагревании. Для расчета теплоты используют понятие теплоемкости (С)

, (В)

где  бесконечно малое количество теплоты, сообщенное системе для изменения ее температуры на . Теплоемкость  экстенсивное свойство. Теплоемкость зависит от природы вещества, его агрегатного состояния, от температуры. На рисунке показана в общем виде зависимость мольной изобарной теплоемкости вещества от температуры.

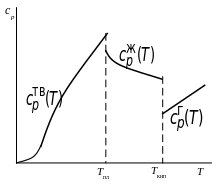
Зависимость изобарной

теплоемкости вещества

от температуры

Эта зависимость получается при подстановке произвольных значений температуры в эмпирически наблюдаемые и приведенные в справочной литературе температурные ряды

, (Г)

где  эмпирические коэффициенты.

При температуре системы, меньшей чем температура плавления (Т < Т ^пл), температурная зависимость теплоемкости вещества имеет вид

. (Д)

При температуре, находящейся в интервале от температуры плавления до температуры кипения (T ^пл <Т < Т ^кип), вещество будет в жидком состоянии и температурная зависимость теплоемкости будет следующей:

. (Е)

И, наконец, при температуре системы выше температуры кипения вещества (T ^кип <Т), когда вещество находится в газообразном виде, зависимость теплоемкости от температуры имеет вид:

. (Ж)

Для идеальных газов мольная теплоемкость практически не зависит от температуры и равна:

для одноатомных идеальных газов = 3/2 R;

двухатомных идеальных газов = 5/2 R;

нелинейных трехатомных и многоатомных молекул = 3 R.

Для идеальных газов справедливо уравнение Майера

. (И)

Экспериментально обнаружено, что внутренняя энергия идеального газа не зависит ни от объема, ни от давления, т.е.

и .

 Второй закон термодинамики устанавливает критерии необратимости термодинамических процессов: существует функция состояния  энтропия S, которая обладает следующим свойством , причем знак равенства относится к обратимым процессам, а знак больше  к необратимым.

Для изолированных систем второй закон утверждает, что энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0).

В отличие от многих других термодинамических функций, энтропия имеет точку отсчета, которая задается постулатом Планка: при абсолютном нуле T = 0 К все идеальные кристаллы имеют одинаковую энтропию, равную нулю.