§5. Диференціал довжини кривої (диференціал дуги)

Розглянемо криву , визначену параметричними рівняннями (4.1):

Позначимо через точку на кривій з декартовими координатами , а через точку з координатами .Через позначимо точку на кривій з координатами . Тоді довжина частини кривої , де визначається за формулою

.

Зрозуміло, що і . Якщо , то диференційовна функція і

.

Звідки, як неважко перевірити,

,

або

, (5.1)

де .

Зокрема, якщо за параметр вибирається довжина змінної дуги, тобто , то із (5.1) маємо

(5.2)

Таким чином, якщо , то:

(5.3)

(5.4)

(5.5)

Для кривої , що належить простору і визначена формулами (4.6) аналогічно маємо:

. (5.6)

§6. Об’єм тіла. Об’єм тіла обертання

Розглянемо множину точок простору , обмеженою замкненою без перетинів поверхнею. Таку множину називають тілом. Як відомо, обчислення об’єму многогранника зводиться до обчислення об’єму трикутних пірамід (тетраїдрів), а тому вважаємо, що об’єм многогранника відомий. Розглянемо всілякі многогранники, вписані і описані навколо тіла : . Символом позначають об’єм тіла, через позначимо точну верхню (нижню) грань множини .

Означення. Тіло називають кубіруємим, якщо і це число називають об’ємом тіла і позначають через .

Нагадаємо, що циліндром називають тіло, обмежене циліндричною поверхнею з образующими, які паралельні деякій осі, двома площинами, перпендикулярними цій осі. Ці площини в перетині з циліндричною поверхнею утворюють плоскі фігури, які називають основами циліндра, а відстань між основами − висотою циліндра.

Нехай тіло в координатному просторі обмежене зліва площиною , а справа − , причому відома площа плоскої фігури, яка є перетином тіла площиною .

Нехай розбиття відрізка точками . Проведемо площини і розглянемо частину тіла , обмежену площинами . Довільним чином виберемо , проведемо площини , в перетині з одержимо плоску фігуру, площа якої . Якщо мале, то зрозуміло (рис.11), що

,

а тому об’єм

За умовою, що , можна показати, що кубіруєме тіло і

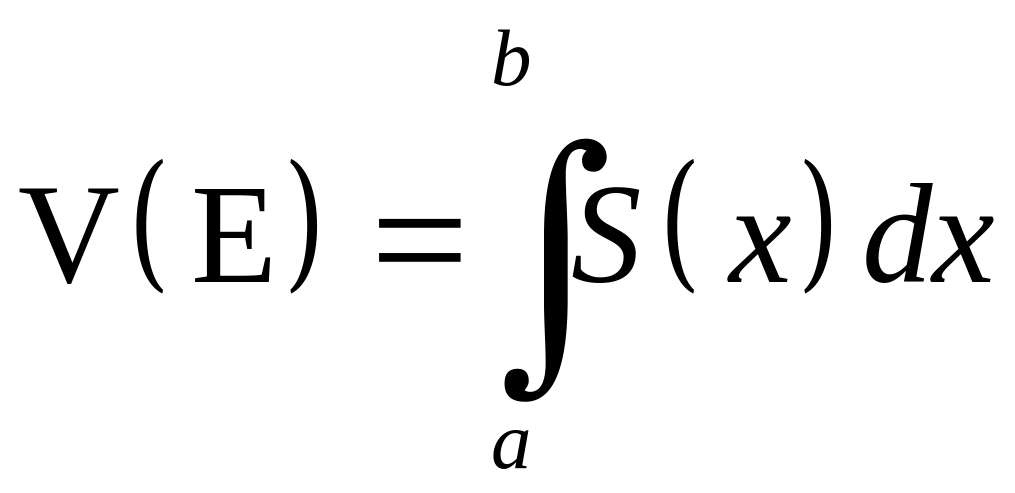(6.1)

Цю формулу називають формулою обчислення об’єму за відомою площею плоских перетинів.

Приклад 6.1. Знайти об’єм тіла, обмеженого поверхнею об’єм еліпсоїда.

Розв'язання. Плоский перетин еліпсоїда площиною є еліпс

з півосями .

Як відомо, площа цього еліпса дорівнює , а тому за формулою (6.1) маємо

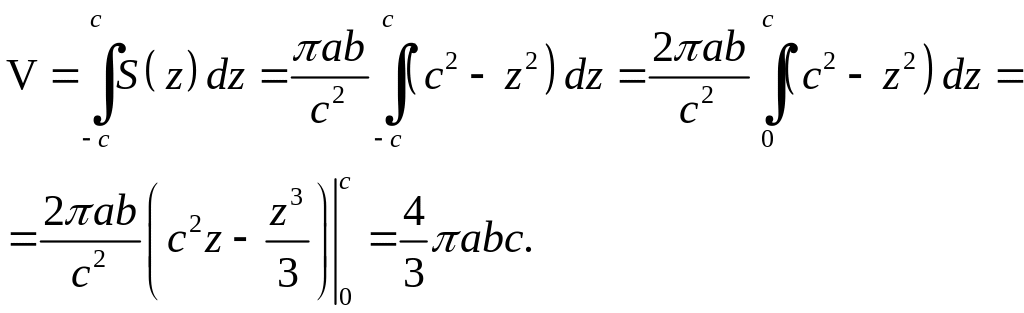
Нехай тепер тіло одержане обертанням навколо осі криволінійної трапеції (рис.12). Тоді будь-який переріз перпендикулярний до осі , буде кругом, радіус якого дорівнює .

Оскільки площа круга дорівнює , то за формулою (6.1) маємо

(6.2)

де .

Якщо тіло одержано обертанням навколо осі криволінійної трапеції (рис.13), то

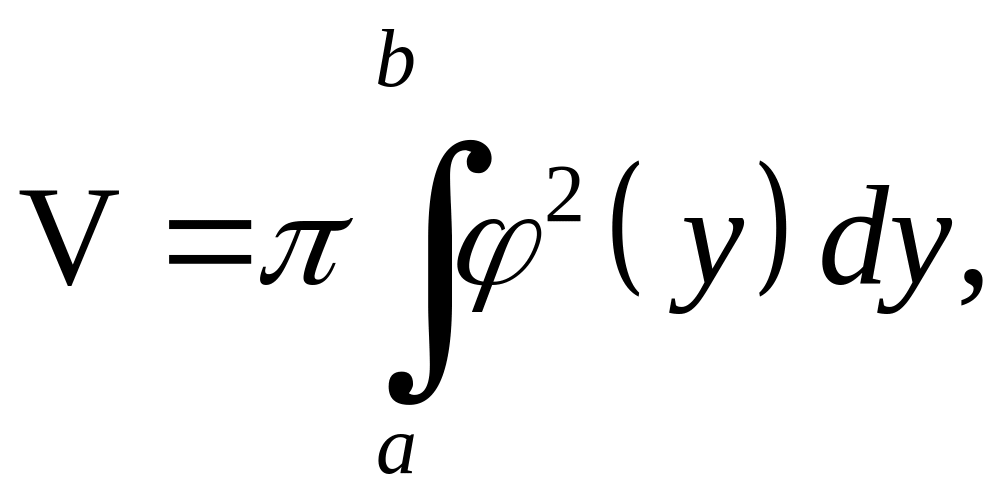(6.3)

Приклад 6.2. Обчислити об’єм тіла обертання фігури, обмеженої еліпсом а) навколо осі ; б) навколо осі .

Розв'язання.

а) оскільки , то за формулою (6.2) маємо

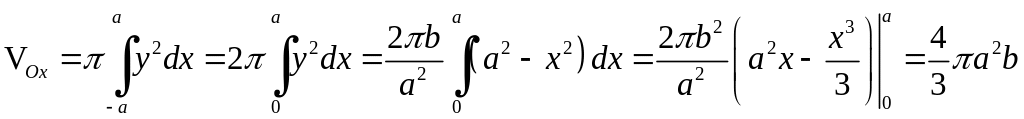
б) в даному випадку і за формулою (6.3) маємо

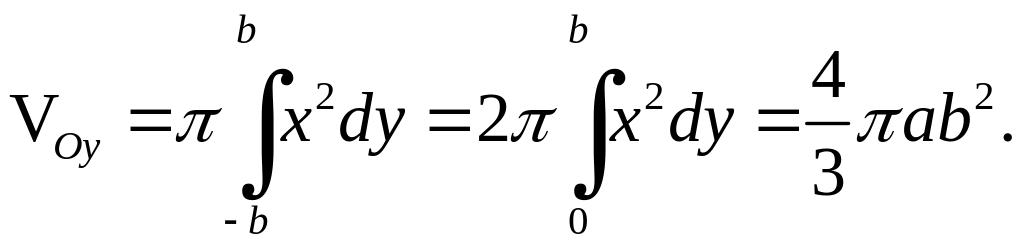
Якщо , то зрозуміло, що

Приклад 6.3. Розглянемо тіло , одержане обертанням круга, обмеженого колом навколо осі . Така поверхня називається тором. Обчислити об’єм тора.

Розв'язання. Зрозуміло, що , де об’єм тіла одержаний обертанням криволінійної трапеції навколо осі , а трапеції навколо тієї ж осі. За формулою (6.2) і властивістю інтеграла

тому що 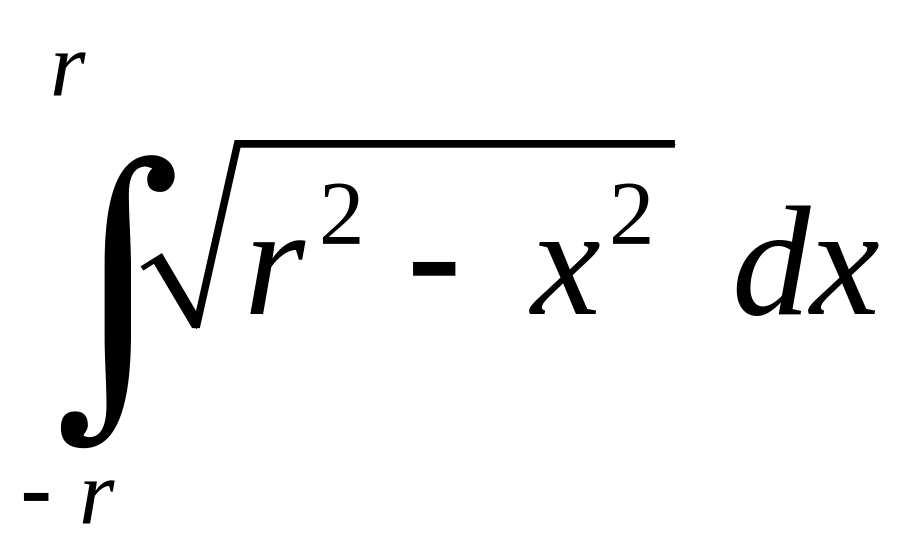за геометричним змістом визначає площу півкола.

Одержаний результат можна сформулювати наступним чином: об’єм тора дорівнює площі круга , помноженій на путь , який пробігає центр ваги при одному обороті навколо осі обертання − відомий як наслідок теореми Гульдіна.