§3. Площа фігури в полярних координатах (площа криволінійного сектора)

Плоску фігуру, обмежену двома променями і і кривою , яка задана полярним рівнянням , , називають криволінійним сектором (рис. 6).

Нехай , .

Згідно зі схемою означення визначеного інтеграла розіб’ємо на частини точками поділу . Виберемо довільним чином і для кожного побудуємо кругові сектори, радіуси яких дорівнюють (рис.6). Як відомо, площа го кругового сектора , а тоді . Зрозуміло, що справа − інтегральна сума для функції , а тому, коли , одержимо

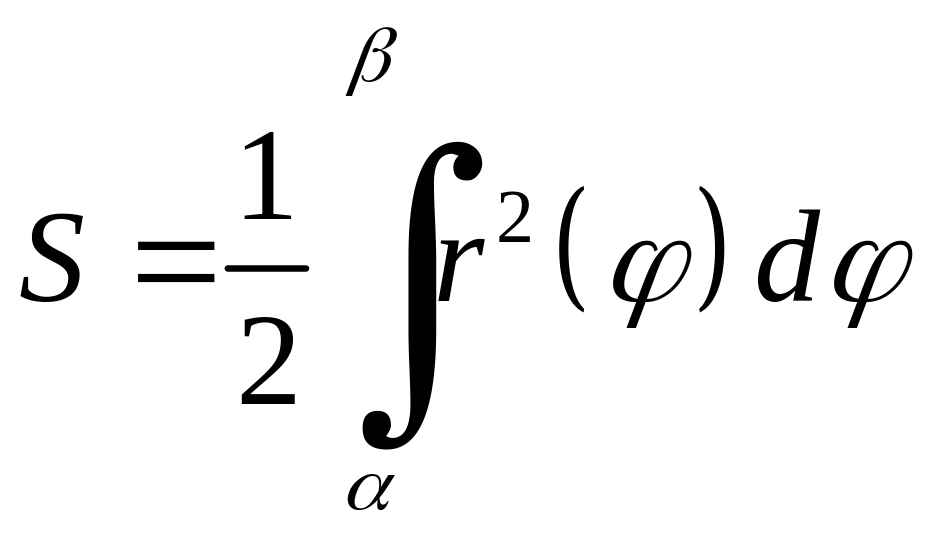(3.1)

Приклад 3.1. Нехай .

Зрозуміло, що , а тому (рис. 7)

.

Рис. 7

При цьому , а тому

.

§4 Крива. Обчислення довжини дуги кривої

Нехай точка рухається на площині і відомий закон її руху , де прямокутні декартові координати точки в момент часу .

Визначимо довжину шляху, який пройде точка за проміжок часу .

Означення 4.1. Шляхом або кривою називають відображення числового проміжку в просторі , яке задається неперервними функціями на проміжку . При цьому називають параметром шляху, а

(4.1)

параметричними рівняннями кривої.

Так, наприклад, криву − півкруг (рис.7) можна записати декартовим рівнянням , а також параметричними рівняннями .

Відмітимо, що рівняння , також визначають той самий півкруг.

У подальшому параметри такі, що або неперервні і строго зростаючі функції.

Означення 4.2. Крива називається простою, якщо двом різним значенням параметра відповідають різні точки на кривій . Точки, що відповідають значенням і параметра , називають граничними точками простої кривої.

Якщо і дві прості криві такі, що

1. граничні точки кривої співпадають з граничними точками кривої ;

2. будь-які не граничні точки кривих і різні,

то крива , одержана як об’єднання кривих і , називається замкненою кривою.

Проста замкнена плоска крива розділяє площину на дві частини − внутрішню і зовнішню.

Відмітимо, що крива може допускати і самоперетин. Прикладом такої кривої є лемніската Бернуллі, (рис. 8), рівняння якої

.

Зрозуміло, що ця крива є об’єднання чотирьох простих кривих, визначених на окремих проміжках .

Означення 4.3. Нехай функції і неперервні на множині , де інтервал, сегмент, півсегмент.

Кажуть, що рівняння (4.1) параметрично визначають криву , якщо існує система , яка розбиває множину так, що на кожному з сегментів множина значень визначає рівняннями (4.1) просту криву.

Так, рівняння

параметрично визначає криву коло радіуса з центром в .

Нехай тепер крива задається параметричними рівняннями (4.1) і нехай довільне розбиття точками поділу . Позначимо через відповідні точки кривої . Ломану будемо називати ломаною, вписаною в криву . Довжина цієї ломаної дорівнює

.

Означення 4.4. Якщо множина довжин вписаних в криву ломаних, одержаних при різноманітних розбиттях сегмента , обмежена, то криву називають спрямляємою, а точна верхня межа (грань) ( ) називається довжиною дуги кривої і позначається через . Зрозуміло, що .

Існують приклади неспрямляємих кривих, які можна знайти, наприклад, в .

Теорема. (Достатня ознака умови існування довжини дуги кривої і формули для її обчислення). Якщо функції на сегменті мають неперервні похідні, то крива , визначена параметричними рівняннями (4.1), спрямляєма і довжина дуги кривої обчислюється за формулою

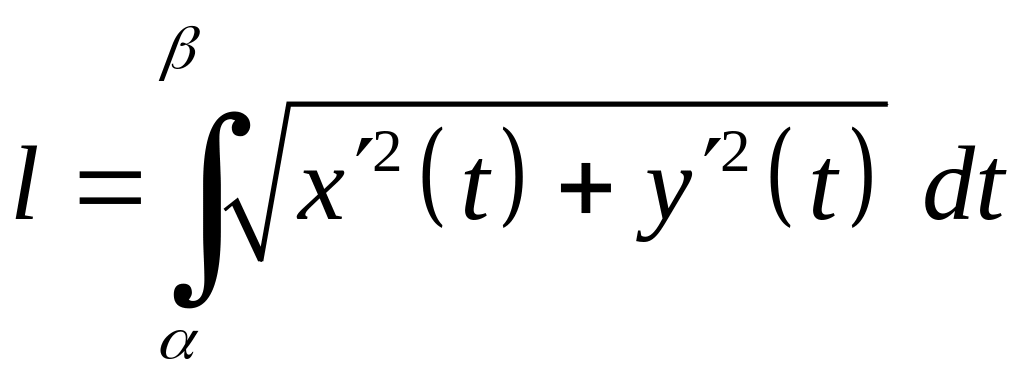(4.2)

Доведення. Оскільки функції задовольняють умовам теореми Лагранжа (див. Основні теореми диференціального числення ), то

За умовою , тому вони обмежені на :

Якщо через позначити , то

,

звідки і слідує, що множина довжин ломаних обмежена зверху, а тому крива спрямляєма.

Відмітимо, що для даного розбиття вираз не є інтегральною сумою для функції тому, що точки нав’язані теоремою Лагранжа, і, крім того, на відрізку вибирається довільним чином одна точка, а не дві . Але можна довести , що за умовами теореми довжина дуги кривої визначається формулою (4.2).

Відмітимо, що для спрямляємості кривої необхідна лише обмеженість на . Більш того, умови теореми можна ослабити, якщо потребувати лише .

Одержимо формули обчислення довжини дуги кривої, визначеної різними способами.

Розглянемо задачу обчислення довжини графіка функції , визначеної на . Відмітимо, що графік функції є крива в . Якщо покласти , то із (4.2) одержимо

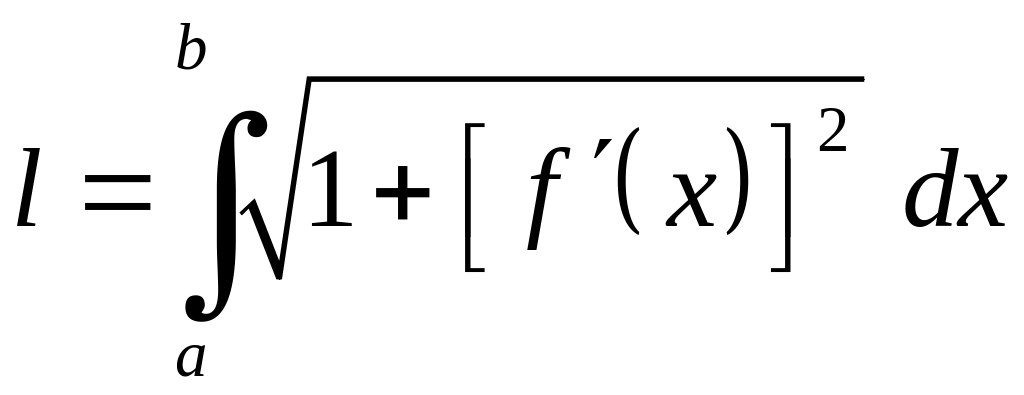(4.3)

Аналогічно, якщо потрібно обчислити довжину дуги кривої на відрізку , то

(4.4)

Якщо крива задана полярним рівнянням , де параметр і

а значить, за формулою (4.2) маємо

(4.5)

Приклад 4.1 Обчислити довжину дуги астроїди (рис. 9). Так називають криву, параметричні рівняння якої .

Рис. 9

Розв'язання. Зрозуміло, що достатньо обчислити довжину дуги кривої, коли (більш того, з урахуванням симетрії відносно прямої можна взяти ):

,

де

А тому

.

Приклад 4.2. Обчислити довжину дуги кривої, визначеної полярним рівнянням (рис. 10, кардіоїда).

Рис. 10

Розв'язання. За формулою (2.5) і враховуючи симетрію графіка, маємо

,

де

Остаточно

.

Приклад 2.3 Обчислити довжину еліпса, визначеного канонічним рівнянням

.

Розв'язання. Враховуючи параметричні рівняння еліпса , одержимо

де .

Інтеграл

не виражається в елементарних функціях, як зазначалось і раніше. Його називають еліптичним. За допомогою таблиць значень функції маємо: довжина еліпса дорівнює .

Зауваження. Якщо крива в просторі визначається параметричними рівняннями

, (4.6)

то довжина дуги кривої визначається за формулою

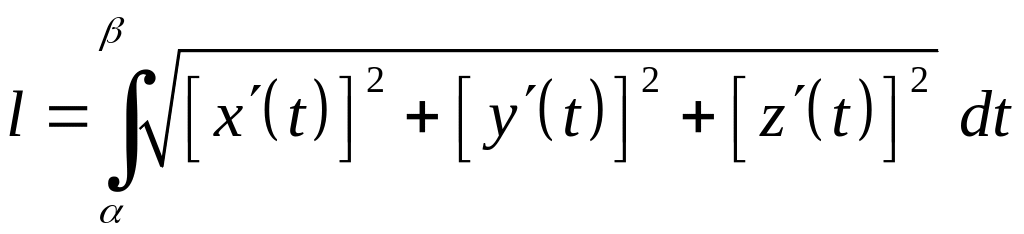, (4.7)

де .