Розділ ііі Застосування визначеного інтеграла до задач геометрії та розв’язку задач з фізики та механіки

§1. Поняття плоскої множини

Розглянемо множину точок площини . Околом точки називають будь-який круг площини, який містить точку , а околом цієї точки називають круг радіуса з центром в точці .

Точку називають внутрішньою точкою множини , якщо існує окіл цієї точки (достатньо малого радіусу ), який цілком належить . Точка називається зовнішньою точкою множини , якщо існує такий окіл точки , який не містить жодної точки із . Точка називається граничною точкою множини , якщо в будь-якому її околі є точки, які належать і є точки, які не належать .

Множину всіх граничних точок називають границею множини і позначають .

Множина називається відкритою множиною, якщо будь-яка її точка внутрішня. Областю називають відкриту множину. Так, наприклад,

відкрита множина, область (круг з центром у точці радіус), її границя.

Плоска множина називається обмеженою, якщо існує круг скінченого радіусу, який містить цю множину. Будемо в подальшому розглядати обмежені області.

Множину називають замкненою.

Із курсу елементарної математики відомо як знайти площу прямокутника, трикутника, трапеції тощо.

Нехай тепер обмежена плоска область. Розіб’ємо її прямими , де . називають рангом розбиття. Так, розбиття го рангу містить квадрати зі сторонами довжини . Позначимо через сукупність квадратів, сторони яких мають довжину , які містяться в , а через сукупність квадратів, які містять . Зрозуміло, що і при цьому площу або міру та легко обчислити, . Аналогічно, розглядаючи розбиття го рангу, одержимо дві послідовності та , причому і

Послідовність обмежена зверху, а знизу, а тому існують

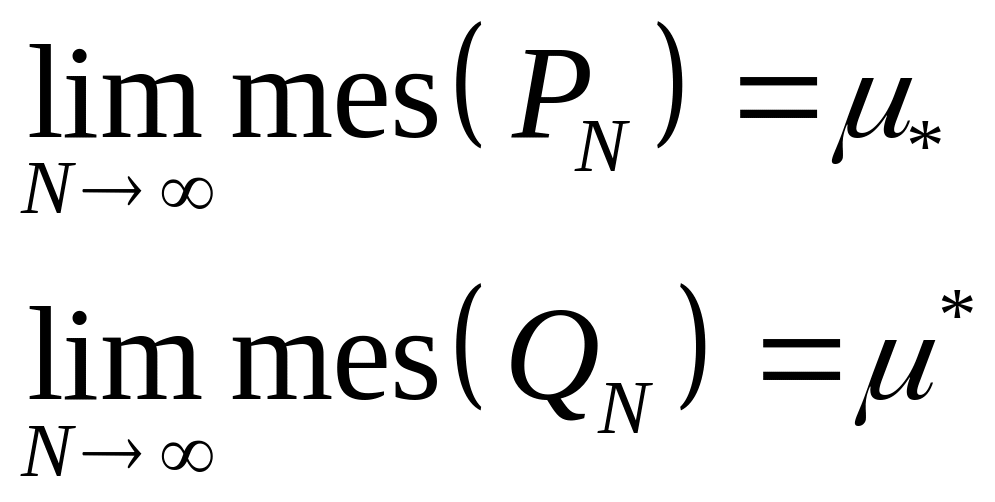
Означення. Обмежена область називається квадрируємою, якщо і число називають площею або мірою області (за Жорданом).

Можна проводити розбиття не обов’язково квадратами, а, наприклад, прямокутниками, трапеціями.

Приклад не квадровної плоскої обмеженої фігури приводиться, наприклад, в .

Справедлива наступна теорема, доведення якої можна прочитати .

Теорема. Для того, щоб плоска фігура була квадровною, необхідно і достатньо, щоб для будь-якого можна вказати такий описаний навколо фігури многокутник і такий вписаний в фігуру многокутник , що

§2. Площа криволінійної трапеції

Із означення визначеного інтеграла маємо: криволінійна трапеція як фігура, що обмежена графіком заданої на неперервної і невід’ємної функції , ординатами, проведеними в точках та відрізком осі між точками і , квадрируєма і її площа обчислюється за формулою

.

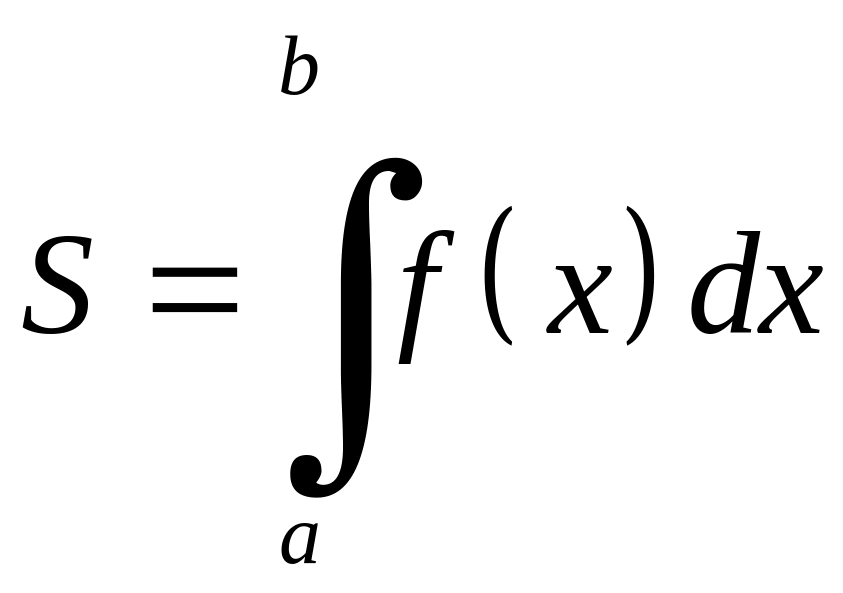Якщо функція неперервна і недодатна на відрізку , то значення інтеграла дорівнює взятій з від’ємним знаком площі криволінійної трапеції, обмеженою графіком функції , ординатами в точках та відрізком осі між точками і . Тому, коли змінює знак, то дорівнює сумі взятих з відповідним знаком площ криволінійних трапецій, розташованих вище і нижче осі , причому, площі перших беруться зі знаком „ ”, а других зі знаком „ ”.

Рис. 1

Взагалі, якщо плоска фігура (рис.1) обмежена знизу графіком функції , а зверху , , то якщо і , то

Приклад 2.1. Знайти площу фігури, обмеженої графіками і (рис. 2).

Розв'язання. Обчислимо координати точок перетину парабол

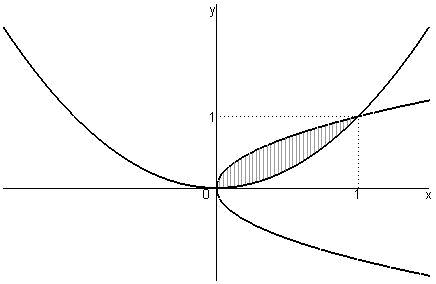
Рис. 2

Тоді, за формулою (2.1), маємо

.

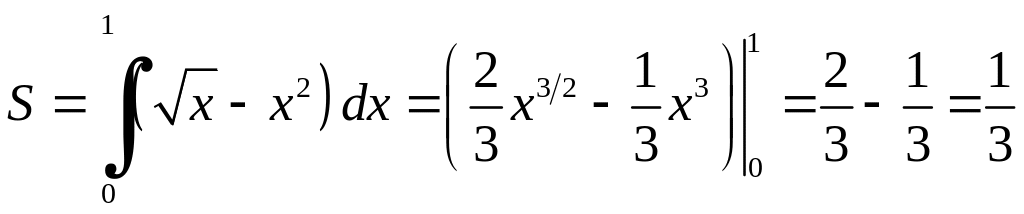Зрозуміло, що площа криволінійної трапеції, обмеженої зліва кривою , справа кривою , де , визначається за формулою

.

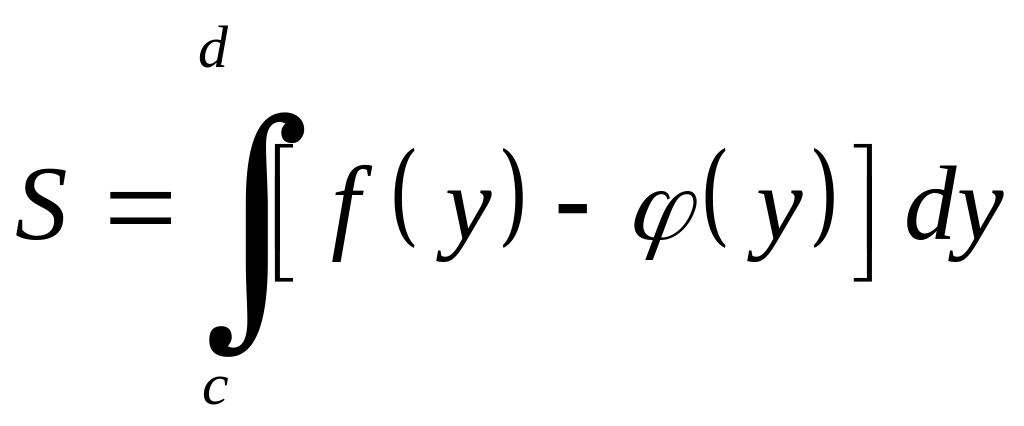Приклад 2.2. Обчислити площу фігури, обмеженої лініями і (рис.3).

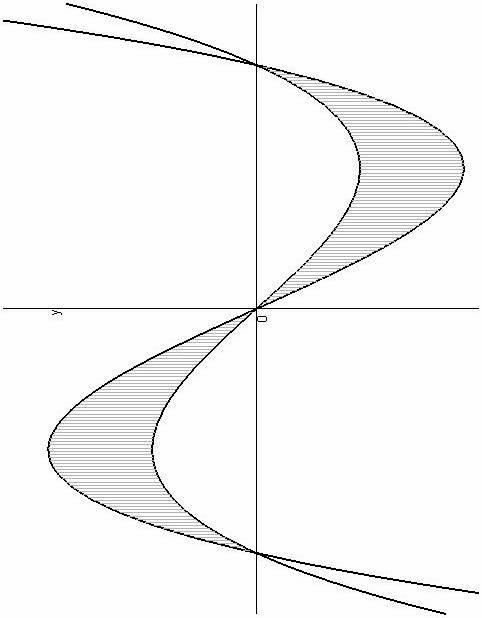
Рис. 3

Розв'язання. Оскільки фігура має дві однакові частини, то

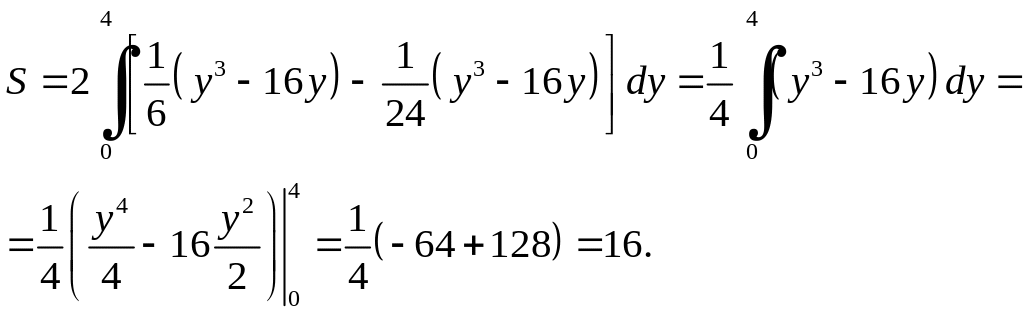
Приклад 2.3. Знайти площу фігури, обмеженої графіками функцій і , прямою і віссю абсцис (рис. 4).

Розв'язання. Обчислимо координати точок перетину парабол

Тоді

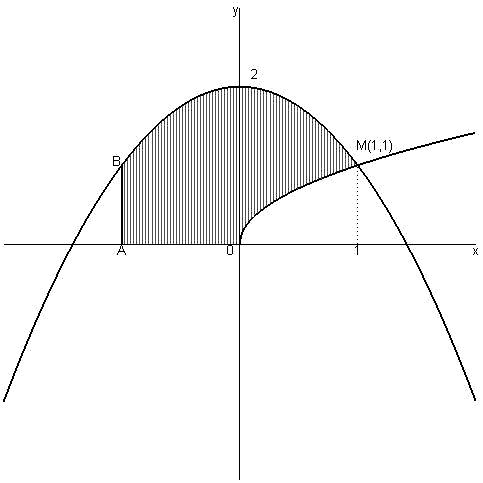
Рис. 4

Приклад 2.4. Поряд з площею круга часто потрібно знати площу еліпса. Виберемо систему координат так, щоб рівняння еліпса мало вигляд .

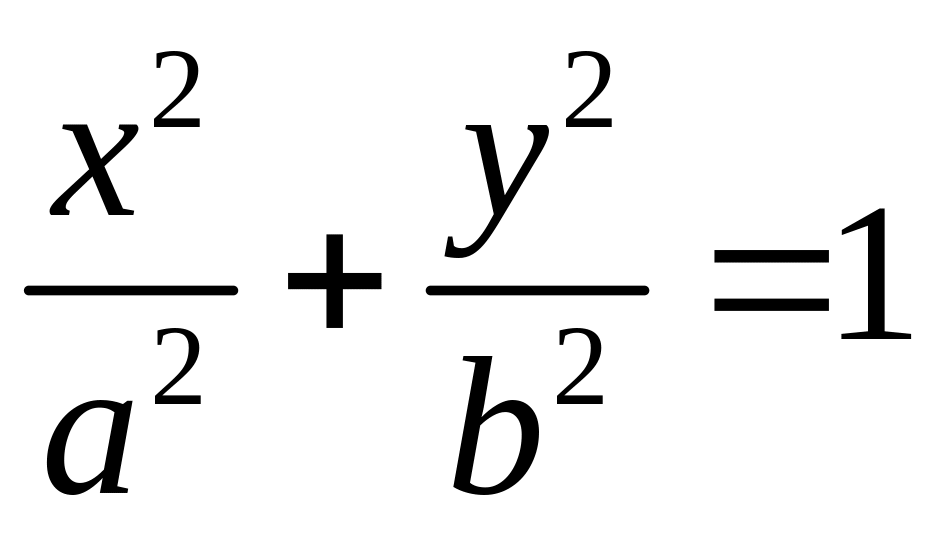Рис. 5

Враховуючи симетрію фігури 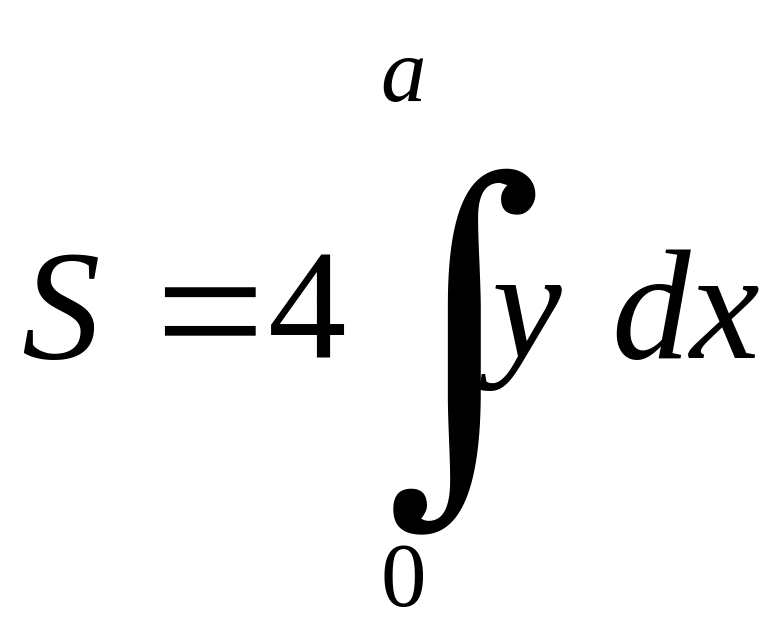, де . Тоді

Зокрема, якщо ( коло), одержимо відомий результат: площа круга радіусу дорівнює .