
- •Физика конденсированного состояния
- •Часть I введение в физику твердого тела
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Устройство и принцип работы спектрометра эпр «Минск-12м»
- •Подготовка к работе
- •Порядок выполнения работы
- •Методика измерений
- •Принцип работы
- •Подготовка измерителя к работе
- •Порядок проведения эксперимента от комнатной температуры
- •Теплопроводность диэлектриков и металлов
- •Физическая основа метода измерения
- •Работа измерителя
- •Общие указания по эксплуатации
- •Подготовка к работе
- •Порядок проведения эксперимента
- •Контрольные вопросы
- •Литература
- •Содержание
- •Часть I
Физическая основа метода измерения
Для измерения теплопроводности в измерителе ИТ-Л-40 использован метод динамического калориметра, теоретическое обоснование которого приводится в литературе [2, 3]. Тепловая схема метода показана на рис. 3.
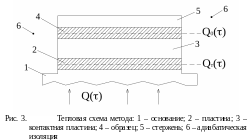 Тепловой
поток
Тепловой
поток
![]() ,
проходящий
через среднее сечение пластины 2, частично
поглощается ею и далее идет на разогрев
пластины 3, образца 4 и стержня 5. Размеры
системы выбраны таким образом, чтобы
потоки, запасенные образцом и пластиной,
были по крайней мере в 5–10 раз меньше
поглощаемых стержнем. В этом случае
температурное поле образца 4 и пластины
2 оказывается близким к линейному,
стационарному; все детали системы
разогреваются с близкими скоростями,
а для потоков и для любого уровня
температуры справедливы формулы:
,
проходящий
через среднее сечение пластины 2, частично
поглощается ею и далее идет на разогрев
пластины 3, образца 4 и стержня 5. Размеры
системы выбраны таким образом, чтобы
потоки, запасенные образцом и пластиной,
были по крайней мере в 5–10 раз меньше
поглощаемых стержнем. В этом случае
температурное поле образца 4 и пластины
2 оказывается близким к линейному,
стационарному; все детали системы
разогреваются с близкими скоростями,
а для потоков и для любого уровня
температуры справедливы формулы:
![]() ,
,
где
![]() – тепловой поток, проходящий через
образец и поглощаемый стержнем, Вт; U0
–
перепад
температуры на образце, К; ρ
–
тепловое сопротивление между стержнем
и контактной пластинкой, м2∙К/Вт;
С0
– полная
теплоемкость образца, Дж/К; Сс
– полная
теплоемкость стержня (медь), Дж/К; b
– скорость разогрева измерительной
ячейки, К/с;
S
– площадь поперечного сечения образца,
м2;
– тепловой поток, проходящий через
образец и поглощаемый стержнем, Вт; U0
–
перепад
температуры на образце, К; ρ
–
тепловое сопротивление между стержнем
и контактной пластинкой, м2∙К/Вт;
С0
– полная
теплоемкость образца, Дж/К; Сс
– полная
теплоемкость стержня (медь), Дж/К; b
– скорость разогрева измерительной
ячейки, К/с;
S
– площадь поперечного сечения образца,
м2;
![]() ,
,
где
![]() – тепловой поток, проходящий через
среднее сечение пластины 2, Вт;
– тепловой поток, проходящий через
среднее сечение пластины 2, Вт;
![]() –
коэффициент пропорциональности,
характеризующий эффективную тепловую
проводимость пластины 2, Вт/К; Uт
–
перепад
температуры на пластине 2, К; Ст
– полная теплоемкость пластины 2 (медь)
, Дж/К; Сп
– полная теплоемкость пластины 3 (медь),
Дж/К.
–
коэффициент пропорциональности,
характеризующий эффективную тепловую
проводимость пластины 2, Вт/К; Uт
–
перепад
температуры на пластине 2, К; Ст
– полная теплоемкость пластины 2 (медь)
, Дж/К; Сп
– полная теплоемкость пластины 3 (медь),
Дж/К.
Тепловое сопротивление между стержнем 5 и контактной пластиной определяется по формуле
P = Pо + Pк,
где Pо – тепловое сопротивление образца, м2∙К/Вт; Pк – поправка, учитывающая тепловое сопротивление контакта, неидентичность и тепловое сопротивление заделки термопар, м2∙К/Вт.
Тепловое сопротивление образца определяется по формуле
![]() ,
,
где h – высота образца, м; λ – теплопроводность образца, Вт/мК.
На основании формул (15) и (18) получены рабочие расчетные формулы для теплового сопротивления образца и его теплопроводности:
![]() ,
,
где
![]() – поправка, учитывающая теплоемкость
образца;
– поправка, учитывающая теплоемкость
образца;
![]() ,
,
Со – полная теплоемкость испытуемого образца, Дж/К;
Сс – полная теплоемкость стержня, Дж/К;
Со = Со(t) mо ,
где Со(t) – ориентировочное значение удельной теплоемкости образца, Дж/кг∙К; mо – масса образца, кг;
Сс = См(t) mс ,
где См(t) – удельная теплоемкость меди, Дж/кг∙К; mс – масса стержня, кг.
Влияние σс обычно принимается 5–10% и может оцениваться по ориентировочным данным теплоемкости образца.
Значение тепловой проводимости пластины определяется по следующей формуле:
![]() .
.
Значение тепловой проводимости образца – по формуле:
![]() .
.
Вычисленные значения теплопроводности образца следует относить к средней температуре образца, которая определяется по формуле:
![]() ,
,
где
![]() – средняя температура образца, С; tc
– температура, при которой проводилось
измерение теплопроводности, С; At
– чувствительность
термопары хромель-алюмель, К/м∙В; По
– перепад
температуры на образце, мВ.
– средняя температура образца, С; tc
– температура, при которой проводилось
измерение теплопроводности, С; At
– чувствительность
термопары хромель-алюмель, К/м∙В; По
– перепад
температуры на образце, мВ.
Параметры Кт и Рк не зависят от свойств испытуемого образца, являются «постоянными» измерителя. Значение Рк обычно дано для материалов с λ = 2–5 Вт/мК и не превышает 10–12% теплового сопротивления образца.
Определение Кт и Рк проводится в градуировочных экспериментах с образцовой мерой из кварцевого стекла и образцом из меди; в данной работе эти величины относятся к табличным. Для определения теплопроводности образца λ в эксперименте необходимо на разных уровнях температуры измерить Uо и Uт (или По и Пт в мкВ).
