
3.5 Циклические коды
Сразу хочется отметить, что циклический код – это одна из самых ярких иллюстраций того, как разумное приложение результатов абстрактной математической теории позволило создать весьма простые и эффективные технические устройства – кодеры и декодеры.
Циклический код – это разновидность линейных блочных кодов, поэтому для него справедливо все, что было сказано в разделах 3.1 и 3.2. В частности, сумма двух комбинаций, взятых из кодовой таблицы, дает комбинацию, принадлежащую той же таблице. Циклические коды обладают еще одним, дополнительным признаком: комбинация, полученная после циклической перестановки символов в последовательности, взятой из кодовой таблицы, принадлежит той же таблице.
Стимулом для создания таких кодов явилось желание использовать для кодирования и декодирования простые устройства, подобные линейным цифровым фильтрам (разд. 2.7).
Поэтому и здесь для описания n-разрядных комбинаций s, состоящих из M-ичных символов, удобно использовать полиномы (2.13)
|
(3.36) |
где sj=0; 1;…; M-1.
Сразу следует запомнить те особые правила обращения с полиномами, которые обусловлены особыми свойствами циклических кодов по сравнению с другими цифровыми последовательностями.
Во-первых, мы ограничимся изучением лишь двоичных кодов, когда любой символ sj в любой точке тракта передачи может принимать лишь одно из двух значений: 0 или 1 (кстати, общая теория циклических кодов охватывает и недвоичные коды, причем при больших значениях M код приобретает некоторые новые свойства, но эта теория, естественно, несколько сложнее). Чтобы обеспечить это ограничение, суммирование символов (коэффициентов полиномов) нужно проводить по модулю 2 (смотри формулы (2.1)). В дальнейшем, ради простоты, будем использовать знак обычного суммирования, например,
x+x=x(1+1)=0,
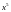 +
+
=
,
+
+
=
,
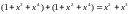 .
.
Во-вторых, циклический код блочный, следовательно, сигналы, получаемые в результате любых преобразований, - это комбинации, состоящие из n бит. Поэтому при умножении полиномов принято соглашение
|
(3.37) |
где
m
– любое целое неотрицательное число,
следовательно,
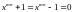 ,
,
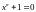 ,
,
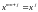 и т.д.
и т.д.
Например,
при n=5
имеем
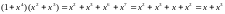 .
В итоге любой полином будет содержать
члены с x
в степени, не превышающей n-1.
.
В итоге любой полином будет содержать
члены с x
в степени, не превышающей n-1.
Итак, при умножении полиномов используются соглашения о суммировании mod 2 и (3.37), а правила деления полиномов, разумеется, вытекают из правил их умножения.
Поскольку
коэффициенты полиномов – целые (двоичные)
числа, при делении полинома на полином
получаем полином-частное и полином-остаток.
Например, при n=5
после выполнения операции
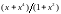 имеем частное
имеем частное
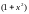 и остаток
и остаток
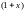 .
В отличие от случая фильтрации обычных
сигналов (разд. 2.7) при работе с циклическим
кодом не имеет значения, каким получилось
частное, важно лишь, каково значение
остатка. Для обозначения полинома,
соответствующего остатку от деления
a(x)
на b(x),
будем использовать один из двух вариантов:
.
В отличие от случая фильтрации обычных
сигналов (разд. 2.7) при работе с циклическим
кодом не имеет значения, каким получилось
частное, важно лишь, каково значение
остатка. Для обозначения полинома,
соответствующего остатку от деления
a(x)
на b(x),
будем использовать один из двух вариантов:
res(x) или a(x)mod b(x), |
(3.38) |
при этом видно, что максимальный показатель степени полинома res(x) не превышает p-1, где p – степень полинома b(x).
В частности, и соглашение (3.37) означает, что завершающая операция над полиномом a(x), полученным в результате каких-либо преобразований, - это вычисление остатка
|
(3.39) |
Другая
особенность, вытекающая из формул (3.37)
и (3.39), заключается в том, что циклическая
перестановка символов вправо в n-разрядной
комбинации отображается умножением
соответствующего полинома на x.
Например, при n=7
для комбинации s=0110011,
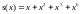 после циклической перестановки имеем
после циклической перестановки имеем
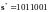 ,
то есть
,
то есть
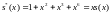 .
.
Способы кодирования и декодирования конкретным циклическим кодом полностью определяются его производящим (порождающим, генераторным) полиномом степени r
|
(3.40) |
где
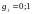 ,
причём всегда
,
причём всегда
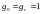 .
Формально этот полином тоже содержит
n
членов, просто у него
.
Формально этот полином тоже содержит
n
членов, просто у него
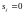 при
при
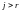 .
.
Фундаментальное свойство циклического кода состоит в том, что полином s(x), соответствующий любой разрешённой (передаваемой) комбинации s, делится без остатка на производящий полином
|
(3.41) |
Отсюда
следует метод декодирования принимаемой
комбинации v(x):
нужно вычислить остаток res(x)
от деления этого полинома на g(x).
Степень полинома res(x)
не превышает r-1,
то есть этот остаток содержит r
бит. Если оказалось, что
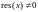 ,
то это несомненно указывает на наличие
ошибок в принятой комбинации (обнаружение
ошибок).
,
то это несомненно указывает на наличие
ошибок в принятой комбинации (обнаружение
ошибок).
Напомним, что переданная s и принятая v комбинации связаны соотношение (3.2), откуда следует
v(x)=s(x)+e(x), |
(3.42) |
где e(x) – полином ошибок. Тогда с учётом (3.41) имеем соотношение, аналогичное формуле (3.17),
res(x)=v(x)modg(x)=s(x)modg(x)+e(x)modg(x)=e(x)modg(x), |
(3.43) |
то есть величина остатка не зависит от того, какая комбинация была передана, а зависит лишь от того, какие произошли ошибки. Таким образом, остаток res(x), вычисленный при декодировании, обладает тем же свойством, что и синдром c любого линейного блочного кода.
Отсюда
вытекает первое требование, которому
должен удовлетворять “хороший”
производящий полином: если нужно
обнаруживать все ошибки кратности
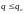 ,
то для всех таких полиномов e(x)
при вычислении по формуле (3.43) должен
получаться ненулевой
остаток.
,
то для всех таких полиномов e(x)
при вычислении по формуле (3.43) должен
получаться ненулевой
остаток.
Из
описанной процедуры декодирования
становится очевидным и способ исправления
ошибок: вычислив остаток для принятой
комбинации v(x),
нужно подставить его значение в уравнение
(3.43) res(x)=e(x)mod
g(x)
и найти из него вектор ошибок e(x).
Тогда очевидно второе требование к
полиному g(x):
если нужно исправлять все ошибки
кратности
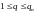 ,
то всем таким полиномам e(x)
должны соответствовать различные
ненулевые остатки, иначе не удастся
однозначно решить уравнение (3.43). Кстати,
максимальное количество различных
ненулевых остатков определяется
очевидным образом
,
то всем таким полиномам e(x)
должны соответствовать различные
ненулевые остатки, иначе не удастся
однозначно решить уравнение (3.43). Кстати,
максимальное количество различных
ненулевых остатков определяется
очевидным образом
|
(3.44) |
а
число различных однократных ошибок
равно n,
число двукратных ошибок равно
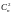 и т.д.
и т.д.
Обратимся к проблеме кодирования. Если полином a(x) степени k-1, соответствующий входной комбинации информационных символов, умножить на производящий полином
s(x)=a(x)g(x), |
(3.45) |
то получим полином, удовлетворяющий условию (3.41) (сравните с формулой (3.21)). Код, формируемый таким образом, не является систематическим.
Для
кодирования
в систематической форме
(информационные символы
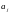 последовательно переносятся в кодовую
комбинацию s
и занимают k
первых позиций) можно применить другой
метод
последовательно переносятся в кодовую
комбинацию s
и занимают k
первых позиций) можно применить другой
метод
|
(3.46) |
Операции, определяемые этим выражением, можно детализировать следующим образом:
1)
умножение a(x)
на
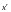 означает, что k
информационных символов сдвигается на
r
позиций вправо и в итоге занимают k
старших (по степеням x)
разрядов; r
разрядов слева при этом оказываются
нулевыми;
означает, что k
информационных символов сдвигается на
r
позиций вправо и в итоге занимают k
старших (по степеням x)
разрядов; r
разрядов слева при этом оказываются
нулевыми;
2)
вычисляется r-разрядный
остаток res(x)
от деления полинома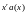 ,
соответствующего полученной таким
образом комбинации;
,
соответствующего полученной таким
образом комбинации;
3) эти r элементов остатка помещаются на r нулевых позиций комбинации, полученной в пункте 1, в качестве проверочных символов.
Легко проверить, что такая комбинация удовлетворяет условию (3.41). Коды, полученные по формулам (3.45) и (3.46), эквивалентны, но это разные коды, то есть им соответствуют разные кодовые таблицы. Но поскольку оба кода обладают одним и тем же свойством (3.41), алгоритмы обнаружения и исправления ошибок для них должны быть одинаковы.
Требования, предъявляемые к полиному g(x) кода, способного обнаруживать и исправлять ошибки заданных кратностей, свидетельствуют, что далеко не всякий полином степени r может быть производящим полиномом. В результате математического анализа, основанного на общих положениях алгебры, было показано, что параметры и производящий полином хорошего циклического кода должны обладать следующими свойствами.
Во-первых,
|
(3.47) |
где
р
– целое число
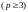 ;
;
|
(3.48) |
где
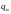 -
максимальная кратность гарантированно
исправляемых ошибок, при этом кодовое
расстояние
-
максимальная кратность гарантированно
исправляемых ошибок, при этом кодовое
расстояние
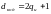 .
При
.
При
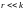 это неравенство обычно обращается в
равенство.
это неравенство обычно обращается в
равенство.
Во-вторых,
|
(3.49) |
для
любого b(x),
если
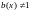 и
и
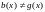 .
Это значит, что многочлен g(x)
является неприводимым (простым), то есть
не делится без остатка ни на какой другой
многочлен, кроме 1 и самого себя.
.
Это значит, что многочлен g(x)
является неприводимым (простым), то есть
не делится без остатка ни на какой другой
многочлен, кроме 1 и самого себя.
В-третьих,
|
(3.50) |
то
есть двучлен
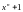 делится без остатка на g(x)
(сравните это с формулой (3.18)).
делится без остатка на g(x)
(сравните это с формулой (3.18)).
Коды, обладающие указанным набором свойств, называются кодами БЧХ. Таблицы производящих полиномов для таких кодов даны в ряде книг [3,4,9,22]. Некоторые из полиномов приведены в Приложении 1.
Обратите
внимание, что при
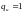 ,
для (3.48) имеем р=r
и для (3.47) получим
,
для (3.48) имеем р=r
и для (3.47) получим
|
(3.51) |
Таким образом, самый простой циклический код БЧХ эквивалентен коду Xэмминга (3.26) и, следовательно, также является оптимальным и совершенным.
Полином степени k, входящий в (3.50),
|
(3.52) |
называется
проверочным
полиномом
данного циклического кода, причём всегда
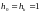 .
Таблицы проверочных полиномов не
приводятся, поскольку его легко можно
найти из (3.50).
.
Таблицы проверочных полиномов не
приводятся, поскольку его легко можно
найти из (3.50).
Вполне естественно, что для кодирования и декодирования вместо полинома g(x) можно использовать полином h(x), при этом фундаментальное свойство (3.41) формулируется следующим образом
|
(3.53) |
то
есть произведение s(x)h(x)
делится без остатка на
,
при этом обозначение
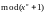 опущено, поскольку эта операция уже
была нами принята в соглашениях (3.37) и
(3.39). Кстати, циклический код – это
линейный блочный код, поэтому неудивительно,
что эта формула напоминает (3.22).
опущено, поскольку эта операция уже
была нами принята в соглашениях (3.37) и
(3.39). Кстати, циклический код – это
линейный блочный код, поэтому неудивительно,
что эта формула напоминает (3.22).
Разумеется, это соотношение также можно использовать для декодирования, то есть для обнаружения ошибок. Итак, и кодер, и декодер можно строить либо на основе производящего полинома, либо на основе проверочного. Во всех случаях кодер и декодер содержат регистр сдвига и сумматоры по модулю 2, причём количество ячеек регистра сдвига равно степени полинома. На практике обычно применяют коды с малой избыточностью, для которых , поэтому кодер и декодер выгоднее строить на основе производящего полинома g(x).
Завершая обсуждение общих положений, отметим, что для кодирования циклическим кодом и декодирования не требуется использования даже производящей и проверочной матриц, не говоря уже о кодовой таблице. Тем не менее, эти матрицы существуют и имеют следующий вид:
|
(3.54) |
где
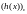 - полином, согласованный с h(x),
то есть коэффициенты этого полинома
записаны в обратном порядке
- полином, согласованный с h(x),
то есть коэффициенты этого полинома
записаны в обратном порядке
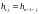 .
Например, при n=7
для
.
Например, при n=7
для
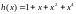 имеем
имеем
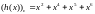 .
.
Рассмотрим
конкретный пример.
Для (n,k)
– кодов с кодовым расстоянием три,
исправляющих все однократные ошибки
(циклических кодов Xэмминга), в Приложении
1 приведены следующие возможные значения
параметров: (7,4), (15,11), (31,26), и т.д.
Проанализируем наиболее короткий код
(7,4). Для него даны два варианта производящего
полинома:
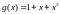 либо
либо
 .
Коды, построенные на основе любого из
них, оказываются разными, но эквивалентными.
Выберем для определённости первый
полином
.
.
Коды, построенные на основе любого из
них, оказываются разными, но эквивалентными.
Выберем для определённости первый
полином
.
Далее найдём проверочный полином из соотношения (3.50),
для
этого выполним деление
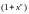 на
на
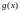 столбиком (рис.3.2).
столбиком (рис.3.2).
Таким
образом, проверочный полином имеет вид
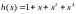 .
.
Пользуясь способом (3.54), запишем производящую и проверочную матрицы
|
(3.55) |
Убедитесь, что эти матрицы удовлетворяют соотношению (3.18).
Схема
кодера, реализующего метод (3.45) в
соответствии с рис. 2.10, приведена на
рис. 3.3. Ячейки регистра обнуляются,
затем при замкнутом ключе K в кодер
вводятся 4 информационных символа, при
этом в схеме вычисляются и выводятся 4
первых символа
 кодовой комбинации. Далее ключ K
размыкается, и в течении следующих трёх
тактов вычисляются и выводятся значения
кодовой комбинации. Далее ключ K
размыкается, и в течении следующих трёх
тактов вычисляются и выводятся значения
 .
.
С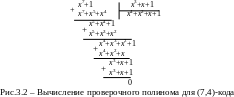 хема
кодера систематического кода, реализующая
метод (3.46), дана на рис. 3.4.
хема
кодера систематического кода, реализующая
метод (3.46), дана на рис. 3.4.
Это
схема деления полинома
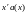 на полином g(x),
но, в
на полином g(x),
но, в
о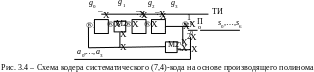
 тличие
от схемы рис.2.11, она построена несколько
иначе, поскольку ориентирована не на
вычисление частного, а на вычисление
остатка. Регистр обнуляется, переключатель
П переводится в положение 2, и в течение
4 тактов в кодер вводят 4 информационных
символа. Одновременно эти символы
поступают на выход в качестве информационной
части кодовой комбинации
тличие
от схемы рис.2.11, она построена несколько
иначе, поскольку ориентирована не на
вычисление частного, а на вычисление
остатка. Регистр обнуляется, переключатель
П переводится в положение 2, и в течение
4 тактов в кодер вводят 4 информационных
символа. Одновременно эти символы
поступают на выход в качестве информационной
части кодовой комбинации
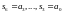 (обратите внимание, что ввод и вывод
производятся в обратном порядке, начиная
с коэффициентов при старших степенях
x).
В это время в регистре с обратными
связями начинается вычисление остатка.
Затем переключатель П переводится в
положение 1, отключая вход, и в течение
следующих 3 тактов завершается вычисление
остатка и его элементы выводятся на
месте проверочных символов кодовой
комбинации
(обратите внимание, что ввод и вывод
производятся в обратном порядке, начиная
с коэффициентов при старших степенях
x).
В это время в регистре с обратными
связями начинается вычисление остатка.
Затем переключатель П переводится в
положение 1, отключая вход, и в течение
следующих 3 тактов завершается вычисление
остатка и его элементы выводятся на
месте проверочных символов кодовой
комбинации
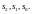
Схема декодера, приведённая на рис. 3.5, также ориентирована на вычисление остатка от деления полинома v(x) на полином g(x) (формула (3.43)), поэтому она практически не отличается от предыдущей схемы. Регистр обнуляется, ключ K замыкается, и в течение 7 тактов в регистр вводятся 7 символов принятой комбинации, начиная с v6 (старшего разряда). После завершения ввода в ячейках регистра оказывается записанным значение остатка res(x). Если res(x)=0 (в 3 ячейках регистра оказались нули), считают, что в принятой комбинации ошибок нет, и на этом декодирование заканчивается.
В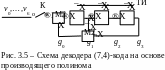 противном случае
противном случае
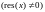 ,
ключ К размыкается (фактически это
соответствует ситуации, когда последующие
входные символы равны нулю), и подают
ещё 7 тактовых импульсов, формально
продолжая процесс деления. Номер такта,
на котором в ячейках регистра оказывается
комбинация 100 (это случай res(x)=1,
учитывается обратный порядок следования
символов), и есть номер ошибочного
символа. После этого исправление этого
символа и отделение информационных
символов – это тривиальные операции.
,
ключ К размыкается (фактически это
соответствует ситуации, когда последующие
входные символы равны нулю), и подают
ещё 7 тактовых импульсов, формально
продолжая процесс деления. Номер такта,
на котором в ячейках регистра оказывается
комбинация 100 (это случай res(x)=1,
учитывается обратный порядок следования
символов), и есть номер ошибочного
символа. После этого исправление этого
символа и отделение информационных
символов – это тривиальные операции.
Чтобы не было сомнений, заметим, что ожидаемая комбинация 100 в течение 7 тактов обязательно появится, причём один раз. Дело в том, что при отключении входа схема рис. 3.5 превращается в генератор двоичной псевдослучайной М-последовательности с периодом (2.21) равным 7. Свойства М-последовательности таковы, что в течение периода в ячейках генератора обязательно по одному разу оказываются записанными все r-разрядные двоичные комбинации, кроме нулевой, разумеется.
Обратите
внимание, что наличие сумматоров на
стыках между ячейками регистра сдвига
определяется значениями коэффициентов
полинома g(x):
сумматор есть, если
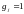 ,
и он отсутствует, если
,
и он отсутствует, если
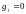 .
Таким образом, зная
g(x), можно сразу составить схемы кодера
и декодера для любого циклического кода
(или схему генератора М-последовательности).
.
Таким образом, зная
g(x), можно сразу составить схемы кодера
и декодера для любого циклического кода
(или схему генератора М-последовательности).
Как
показывает практика, формальное
запоминание приведённых соотношений
и схем мало что даёт для понимания сути
вопроса, если детально не разобрать
хотя бы десяток конкретных численных
примеров. В частности, если нужно
закодировать информационную
последовательность 0011, для которой
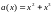 ,
то, проследив такт за тактом работу
схемы рис.3.4 и записывая содержимое
ячеек, можно убедиться в том, что на
выходе появится комбинация 1100010, которой
соответствует полином
,
то, проследив такт за тактом работу
схемы рис.3.4 и записывая содержимое
ячеек, можно убедиться в том, что на
выходе появится комбинация 1100010, которой
соответствует полином
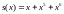 (значение этого полинома вычислите
отдельно по формуле (3.46) и сравните с
комбинацией).
(значение этого полинома вычислите
отдельно по формуле (3.46) и сравните с
комбинацией).
В заключение обязательно нужно отметить следующее обстоятельство. Благодаря циклическому свойству, при кодировании и декодировании циклического кода удаётся организовать конвейерную обработку длинных последовательностей символов в устройствах, содержащих удивительно малое количество простейших логических элементов. Например, для кода (255,247) кодер и декодер содержат по 8 ячеек регистра сдвига и по 4 сумматора по модулю 2. Благодаря этому ценному качеству среди всевозможных линейных блочных кодов именно циклические коды нашли наиболее широкое применение.

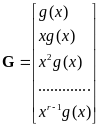 ,
,
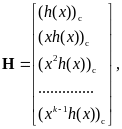
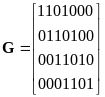 ,
,
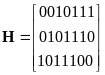 .
.