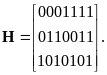3.3 Коды Хэмминга

Продолжим рассмотрение линейных блочных кодов, обладающих кодовым расстоянием и в соответствии с (3.6) способных обнаружить любую одиночную ошибку в принятой n-разрядной комбинации.

Таблица (e–c) типа табл. 3.3 содержит n строк, при этом все значения r-разрядного вектора c должны быть различными. Тогда максимально-возможное значение n определяется формулой

(3.26)

где вычитание единицы обусловлено тем, что нулевая комбинация, соответствующая отсутствию ошибок, в таблице не содержится.

Коды, обладающие такими параметрами, называются кодами Xэмминга. К ним относятся коды (3,1), (7,4), (15,11), (31,26) и т.д.

Кстати, код (5,2), рассмотренный в разделе 3.2, также имеет , но не является кодом Хэмминга.

Напомним, что эта таблица (e-c) построена с использованием формулы , и в ней значения вектора-синдрома совпадает с соответствующими столбцами матрицы H, поэтому даже нет нужды в построении этой таблицы. К сожалению, такое простое соответствие характерно только для кодов, исправляющих одиночные ошибки.

Итак, для кода Хэмминга в качестве столбцов матрицы H нужно записать различные r-разрядные двоичные числа, кроме нулевого (красота идеи построения кода Хэмминга станет позже более понятной, если их записать в порядке возрастания).

Для примера запишем матрицу H для (7,4)-кода

(3.27)

В качестве проверочных для кода Хэмминга можно считать любые r символов, но вычисление их значений при кодировании слегка упрощается, если в качестве проверочных взять те символы, которые охвачены лишь одной проверкой на чётность. В нашем примере это s₁, s₂, s₄, тогда информационными символами будут s₃, s₅, s₆, s₇. Перестановкой символов код можно привести к систематическому виду, но пользы от такой операции в данном случае пока не видно.

Кодирование для (7,4)-кода проводится следующим образом: четыре информационных символа , поступившие на вход кодера, записываются на позиции s₃, s₅, s₆, s₇, а затем находят три проверочных символа по той же методике, как и (3.15)

(3.28)

Декодирование начинается с вычисления синдрома (3.16). Если c=0, считают, что ошибок нет. В противном случае вычисленное значение c совпадает с номером ошибочного символа, записанным в двоичной форме.

Для (7,4)-кода вычисление элементов синдрома проводится по формулам

(3.29)

Например, для принятой комбинации y=0111100 имеем c=000, поэтому считываем значения 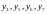и подаём их на выход декодера (проверочные символы свою роль уже сыграли и получателю они не нужны). Для комбинации 1010001 имеем c=101, то есть ошибка в пятом символе – его нужно изменить на обратный (0 на 1).

Код Хэмминга определён формулой (3.26), поэтому он является оптимальным кодом, то есть, среди всех кодов с заданными значениями r и нет другого кода, который бы обладал меньшей избыточностью (3.25). Более того, он относится к классу совершенных кодов, то есть, исправляя любую однократную ошибку, он не способен исправить ни одной ошибки более высокой кратности. Хотя обнаружить он может и однократные, и двукратные ошибки. Поэтому при обнаружении ошибок (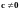 ) дальнейшее декодирование проводится в предположении, что в кодовой комбинации произошла более вероятная, однократная ошибка. Таким образом, совершенство кода заключается в том, что он все ресурсы направляет на исправление однократных ошибок.

Это стремление просматривается в схеме проверок, построенной наиболее рациональным образом, если вспомнить, что результат каждой проверки выдаётся в двоичной форме (да - нет). Представим себе, что перед декодированием комбинация дополнена слева ещё одним знаком , символизирующим отсутствие ошибок в остальных символах. 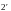Тогда проведение проверок на чётность напоминает процедуру угадывания числа, которое может принять любое из значений. Схема проверок на чётность указывает, каким должен быть смысл каждого из задаваемых вопросов при условии, что на каждый из них даётся ответ “да” или “нет”. Схема проверок кода Хэмминга такова, что позволяет уверенно определить заданное число при минимальном количестве вопросов r.