
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Вопросы для самопроверки
1. Что называется матрицей и расширенной матрицей системы линейных уравнений?
2. Что называется решением системы линейных уравнений? Какие системы называются совместными, а какие – несовместными?
3. Напишите формулы Крамера. В каком случае они применимы?
4. При каком условии система линейных уравнений имеет единственное решение?
5. Что можно сказать о системе линейных уравнений, если ее определитель равен нулю?
6. При каком условии система n линейных уравнений с n неизвестными имеет ненулевое решение?
7. Как определяются линейные операции над матрицами и каковы их свойства?
8. Что называется произведением двух матриц? Каковы свойства произведения матриц?
Задачи для самостоятельного решения
В задачах 1-7 решить системы уравнений:
1.
EMBED Equation.3
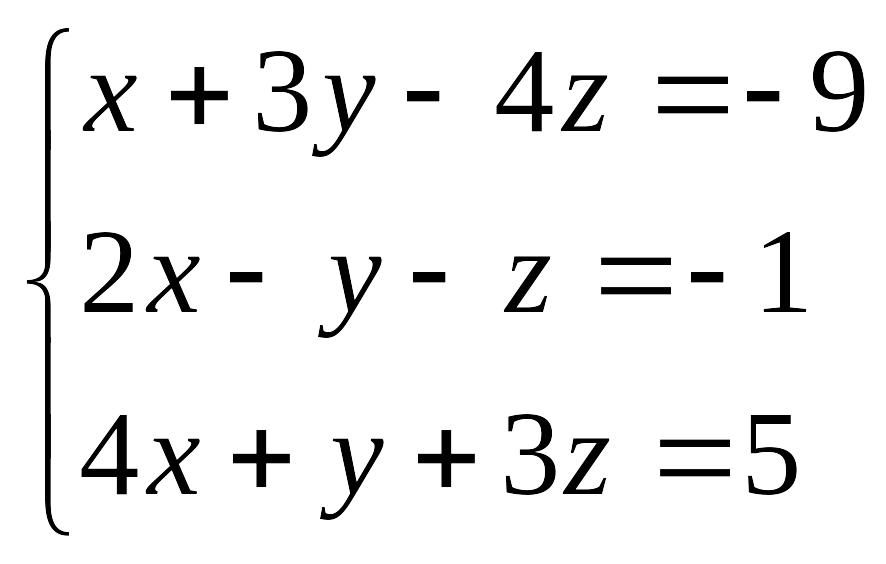 . 2.
EMBED Equation.3
. 2.
EMBED Equation.3
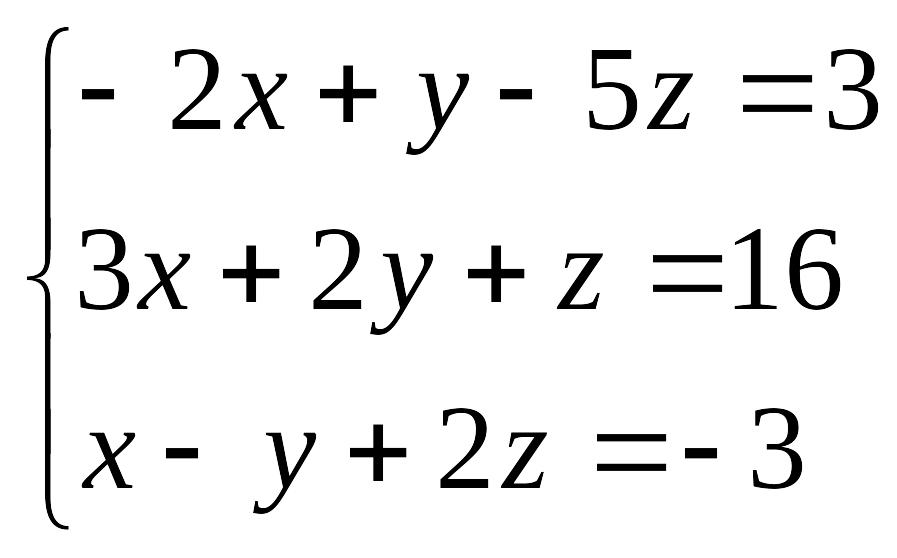 .
.
3.
EMBED Equation.3
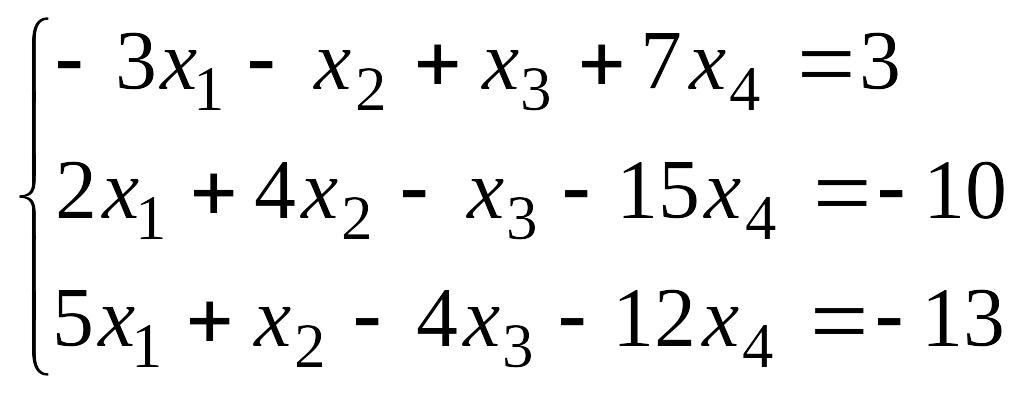 .4.
EMBED
Equation.3
.4.
EMBED
Equation.3
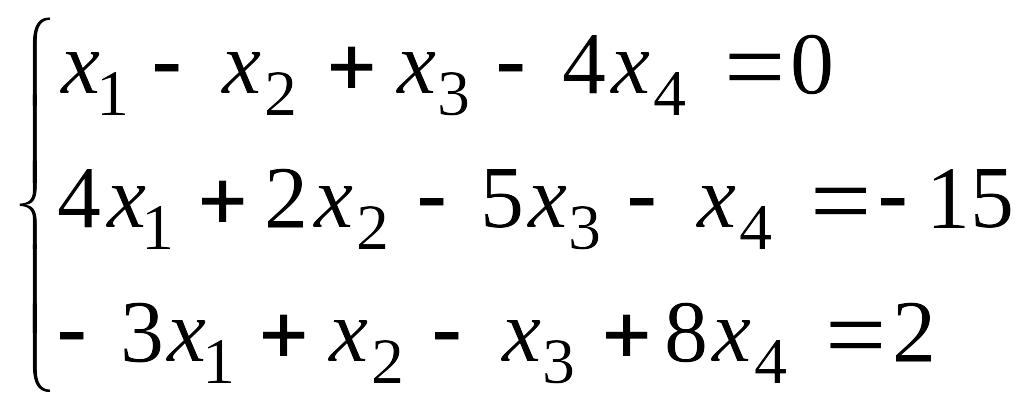 .
.
5.
EMBED Equation.3
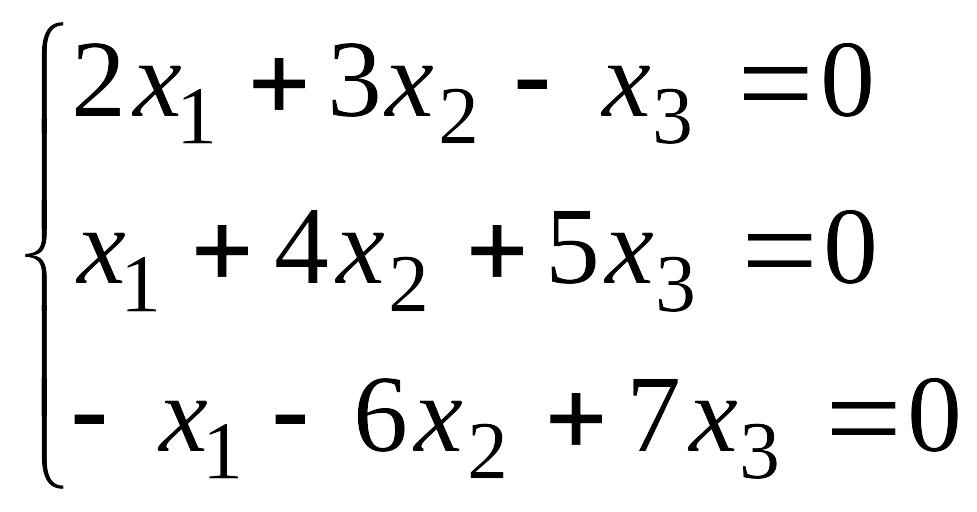 .
6.
EMBED Equation.3
.
6.
EMBED Equation.3
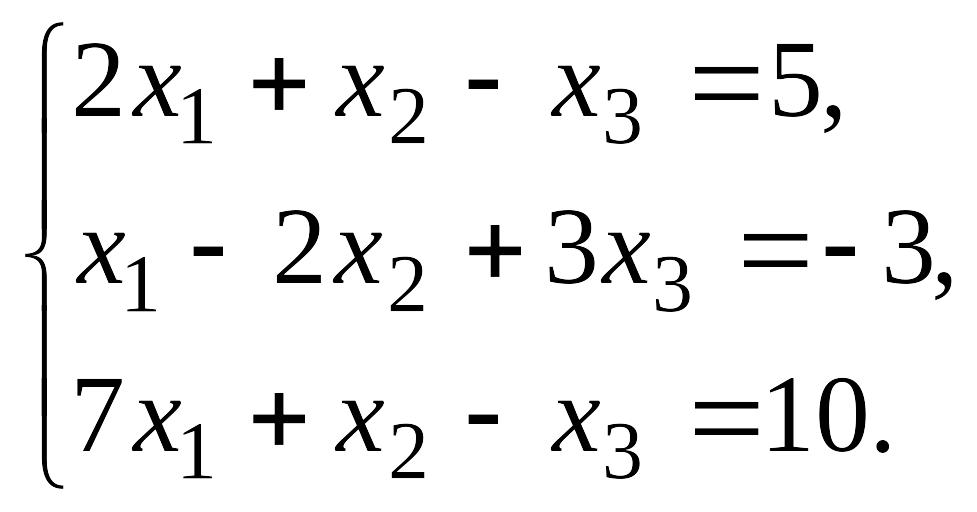
7.
EMBED Equation.3
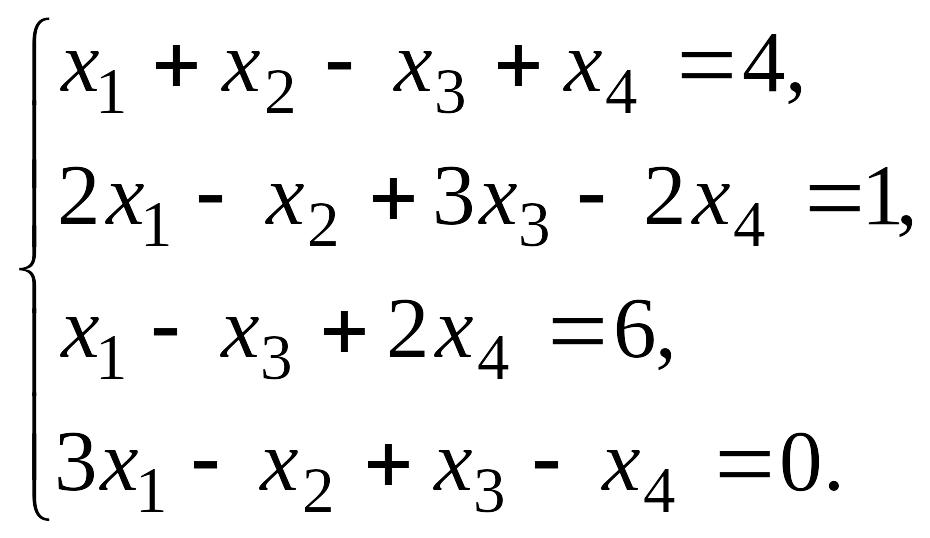
8.Найти сумму матриц
EMBED
Equation.3
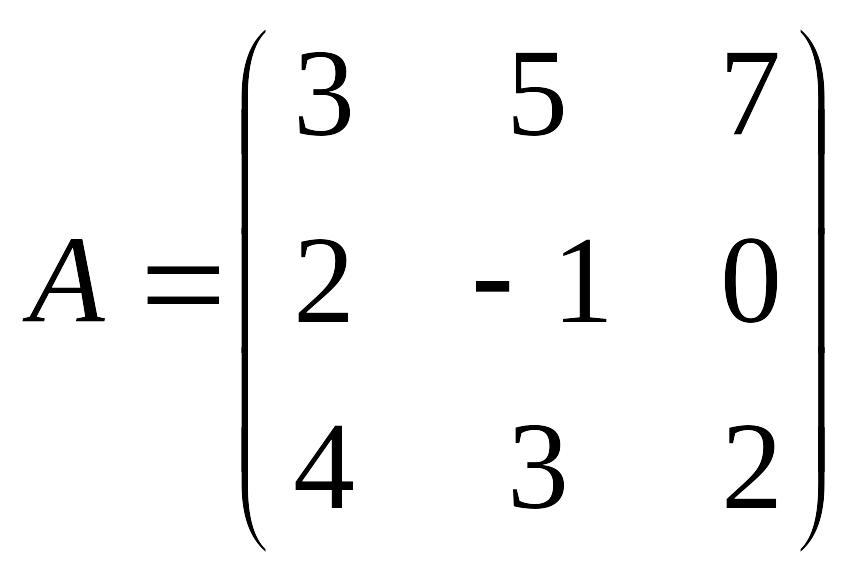 ,
EMBED Equation.3
,
EMBED Equation.3
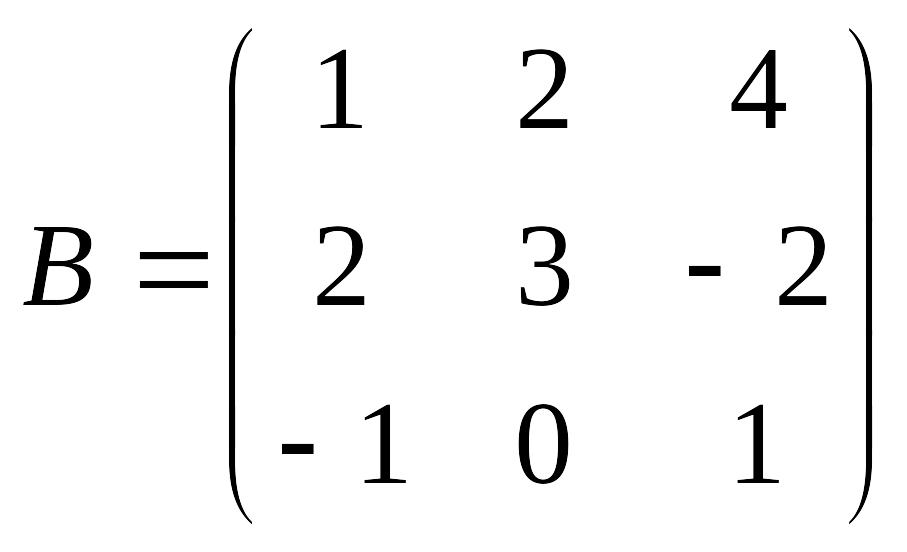 .
.
9. Найти матрицу 2А+5В, если
EMBED
Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() .
.
10.
.Найти
значение матричного многочлена 2А2+3А+5Е
при EMBED
Equation.3
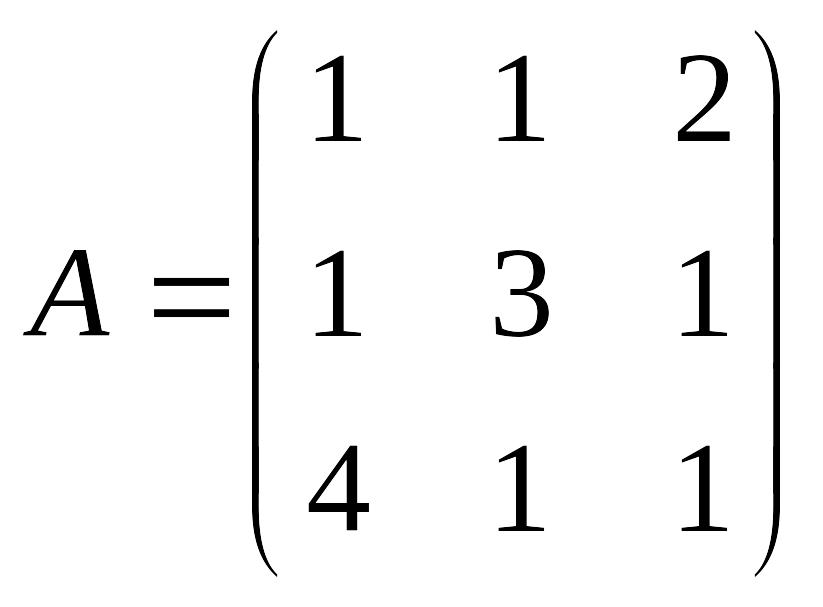 , если Е
–единичная матрица третьего порядка.
, если Е
–единичная матрица третьего порядка.
11.
Найти матрицу
АВ,
если EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() ,
В= EMBED Equation.3
,
В= EMBED Equation.3
![]() .
.
12.
Дана матрица EMBED Equation.3
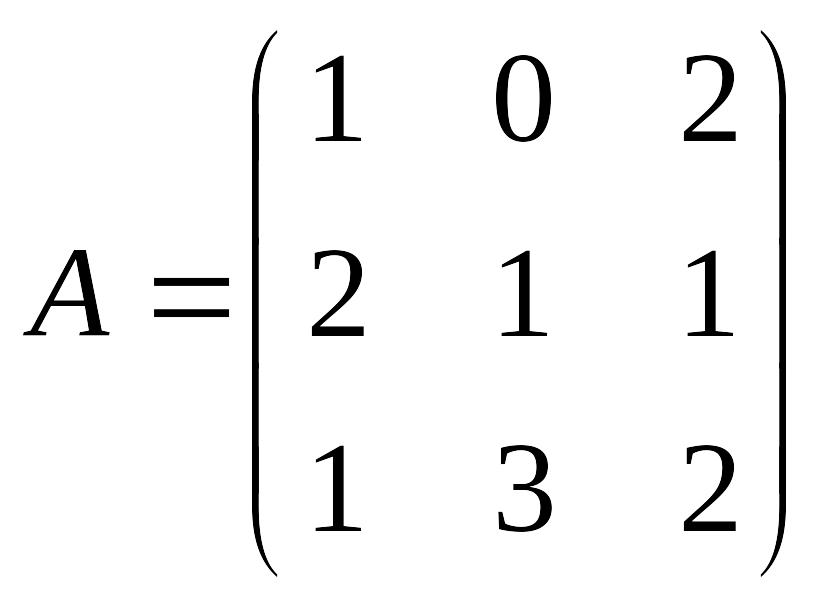 .
Найти матрицу EMBED Equation.3
.
Найти матрицу EMBED Equation.3
![]() .
.
Ответы: 1. (1;-2;1). 2. (3;4;-1). 3. ( 1+t; -2+3t; 4-t; t ).
4.
( -1+2t;
2-t;
3+t;
t
). 5.
( 0; 0; 0 ). 6. (
1 ;5 ;2 ). 7. (
1; 2; 3; 4 ). 8.
EMBED Equation.3
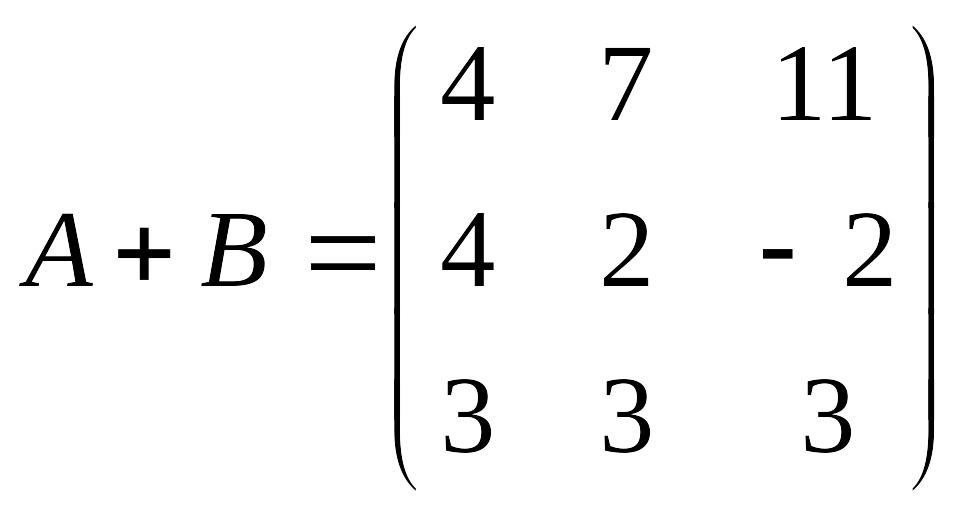 .
9.
EMBED Equation.3
.
9.
EMBED Equation.3
![]()
10.
EMBED Equation.3
 .
11.
АВ= EMBED
Equation.3
.
11.
АВ= EMBED
Equation.3
![]() .
12.
EMBED Equation.3
.
12.
EMBED Equation.3
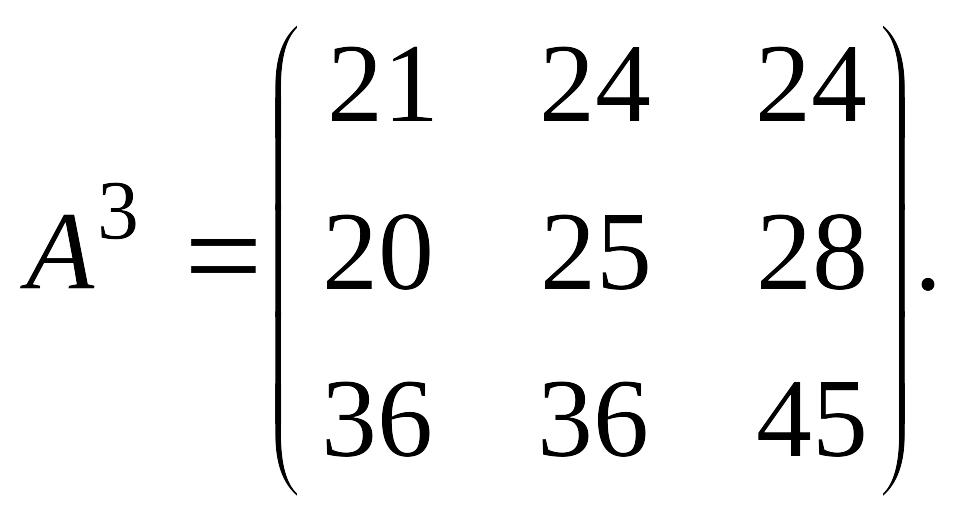
Занятие 3. Ранг матрицы. Вычисление обратной матрицы. Решение систем уравнений с помощью обратной матрицы
3.1. Вычисление ранга матрицы
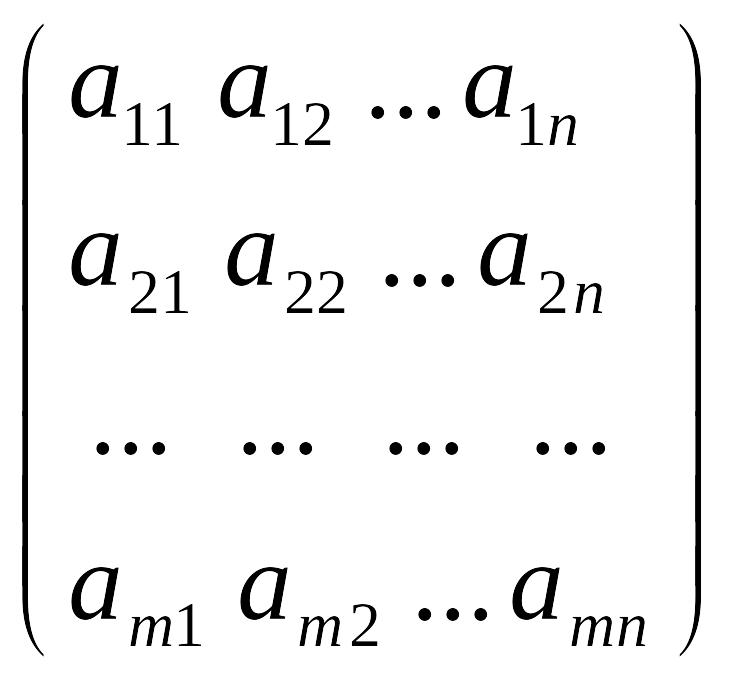
Пусть дана матрица, содержащая m строк и n столбцов
А
= EMBED
Equation.3
 .
.
Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка; определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что в общем случае таких миноров k-го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел m и n, т. е.
max k = min(m,n)
Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь, среди этих миноров можно найти, по крайней мере, один минор наибольшего порядка.
Наибольший порядок миноров, отличных от нуля, называется рангом матрицы .
Для вычисления ранга матрицы приведем ее к ступенчатому виду: Будем изменять матрицу А размера m´n так, чтобы сохранялся ее ранг. В результате матрица приводится к виду:
|
|
m-r{ |

 EMBED
Equation.3
EMBED
Equation.3
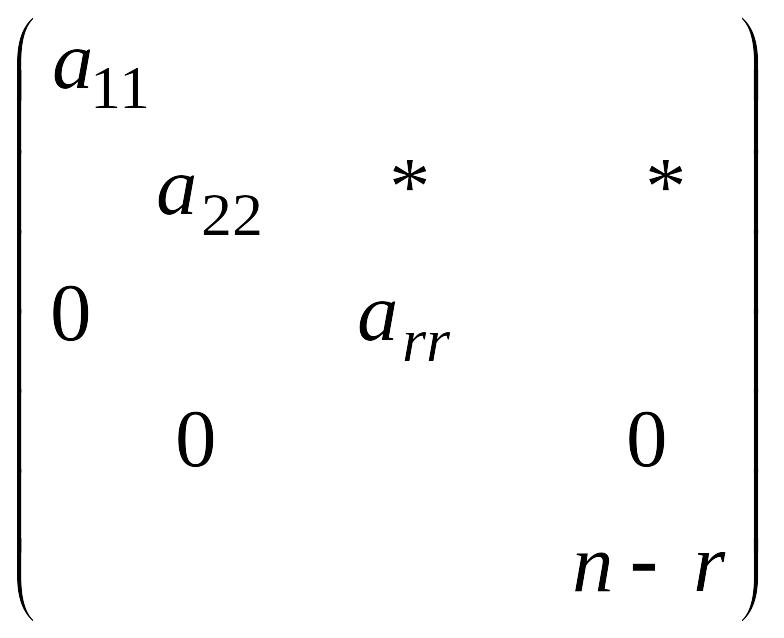 ; EMBED Equation.3
; EMBED Equation.3