
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Типовые расчеты
Типовые расчеты – это самостоятельные домашние работы, которые выполняются студентом после изучения отдельных частей курса высшей математики. Типовые расчеты являются подготовкой к зачетной контрольной работе.
Правила выполнения и оформления типовых расчетов
При выполнении типовых расчетов требуется строгое соблюдение указанных ниже правил.
Работа выполняется в тетради в клетку чернилами любого цвета кроме красного. Необходимо оставлять поля для замечаний преподавателя.
В работу включаются все задачи, указанные в задании, и строго по положенному варианту.
Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
Вариант выбирается в соответствии с порядковым номером студента в списке группы.
После получения проверенной работы исправляются все отмеченные ошибки и работа сдается на повторную проверку.
1 . Матрицы. Определители. Системы линейных уравнений
Задание 1. Решить систему уравнений: 1) по правилу Крамера , методом Гаусса; 2) с помощью обратной матрицы
1.1.
1)
EMBED Equation.3
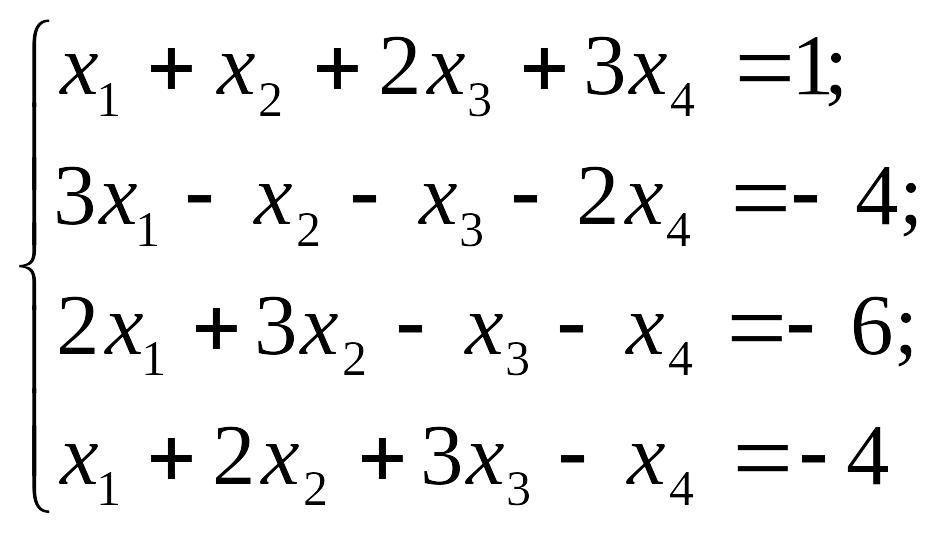 2) EMBED Equation.3
2) EMBED Equation.3
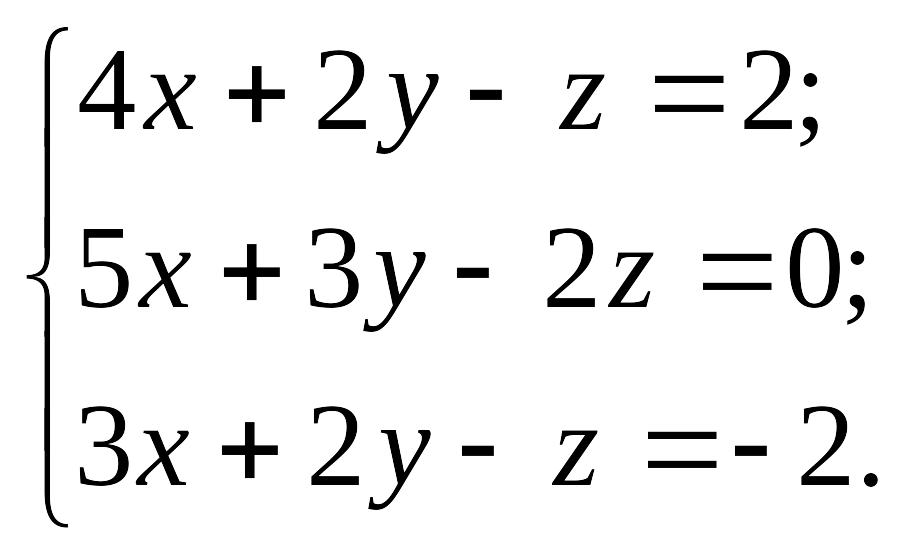 EMBED Equation.3
EMBED Equation.3
1.2.
1)
EMBED Equation.3
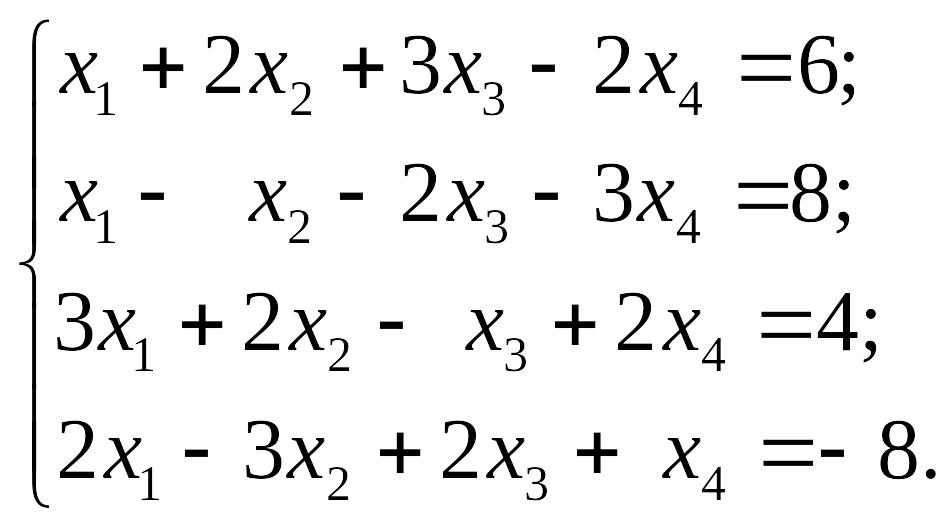 2)
EMBED Equation.3
2)
EMBED Equation.3
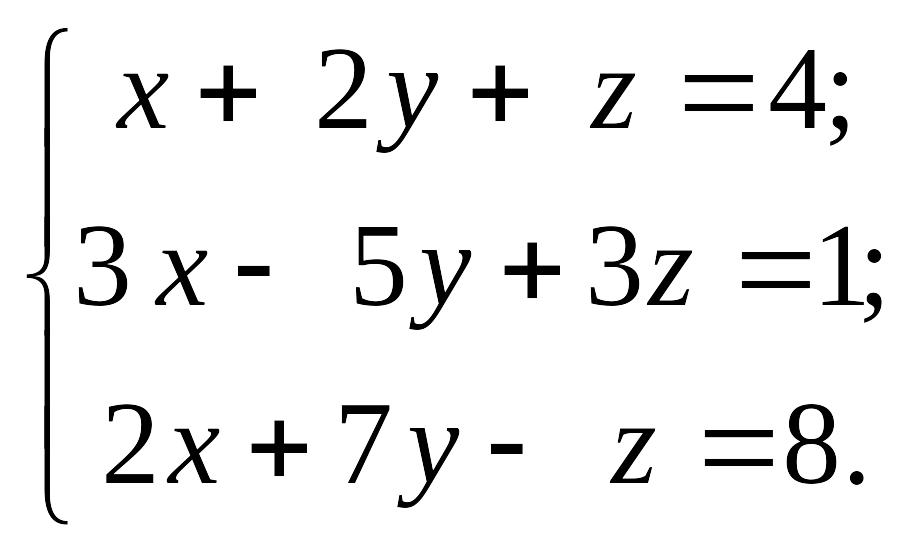
1.4.
1)
EMBED
Equation.3
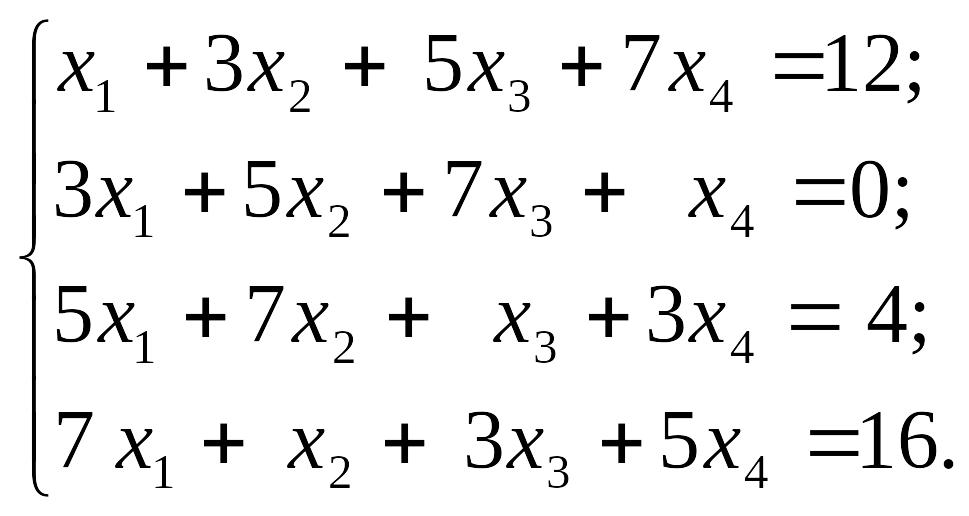 2)
EMBED
Equation.3
2)
EMBED
Equation.3
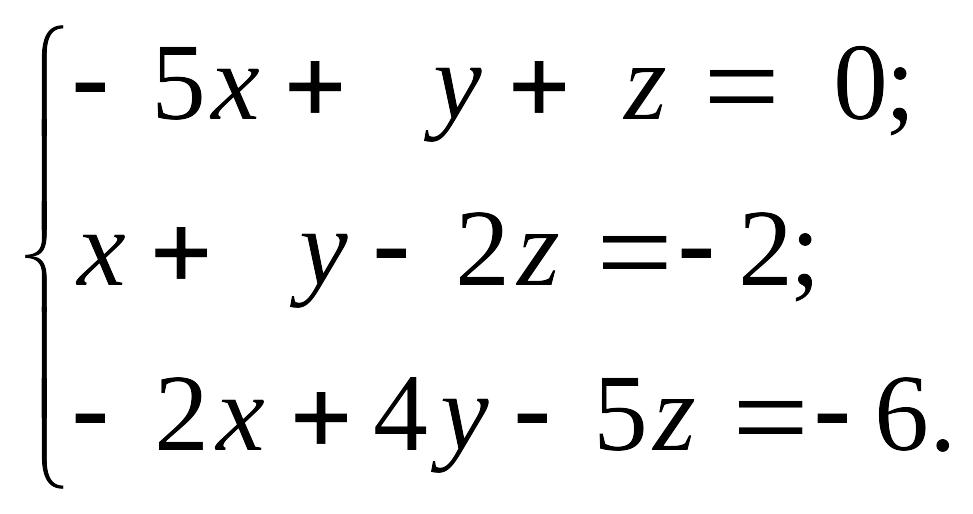
1.5.
1)
EMBED
Equation.3
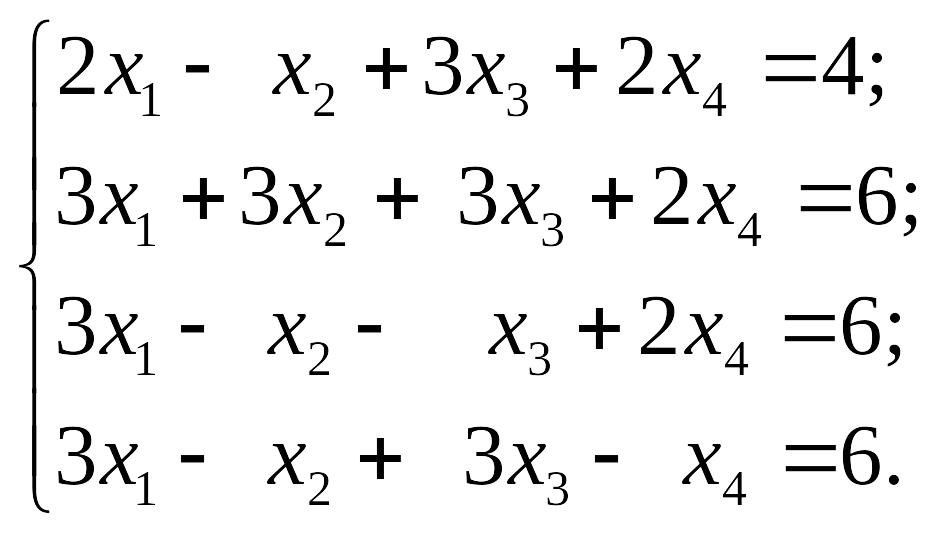 2) EMBED
Equation.3
2) EMBED
Equation.3
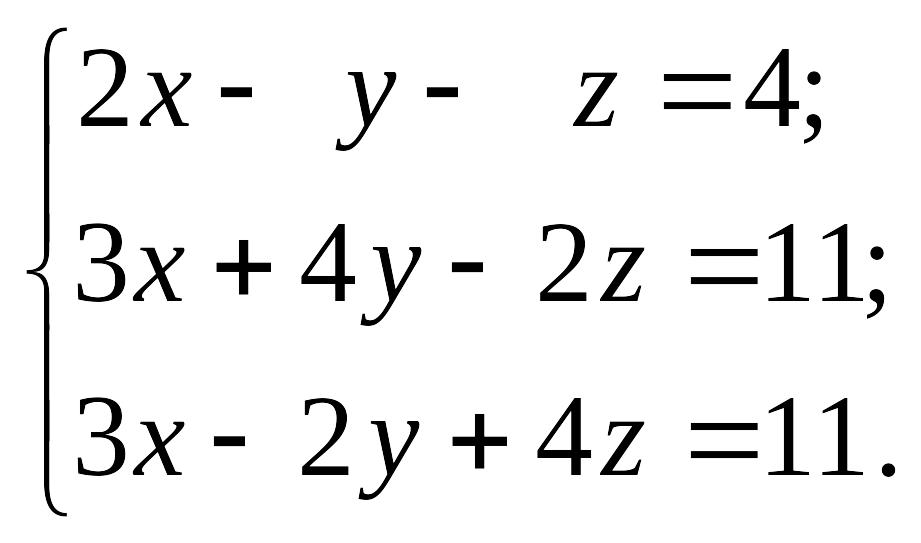
1.6.
1)
EMBED
Equation.3
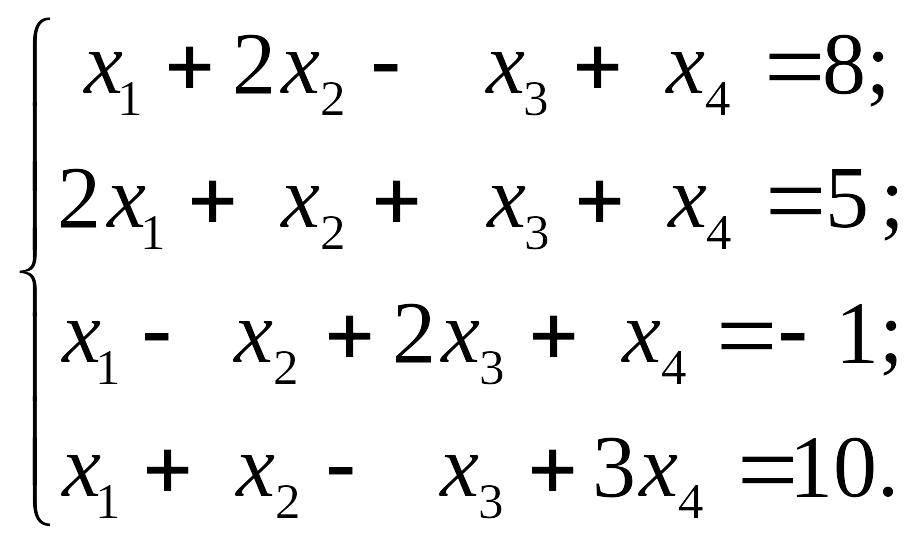 2)
EMBED
Equation.3
2)
EMBED
Equation.3
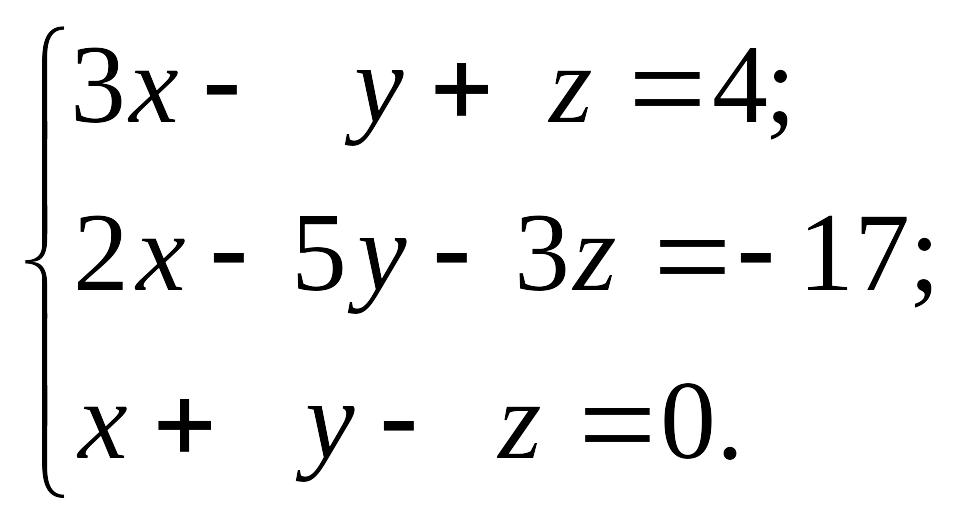
1.7.
1)
EMBED Equation.3
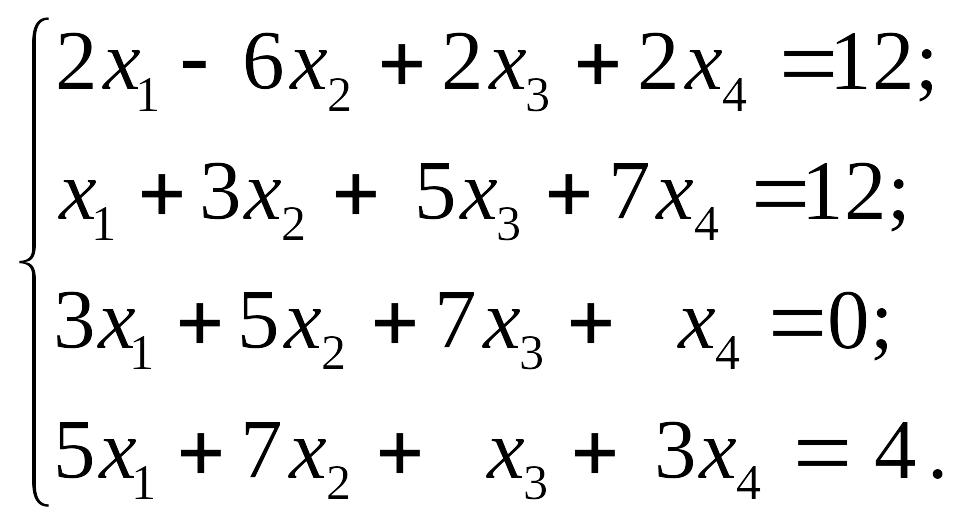 2)
EMBED Equation.3
2)
EMBED Equation.3
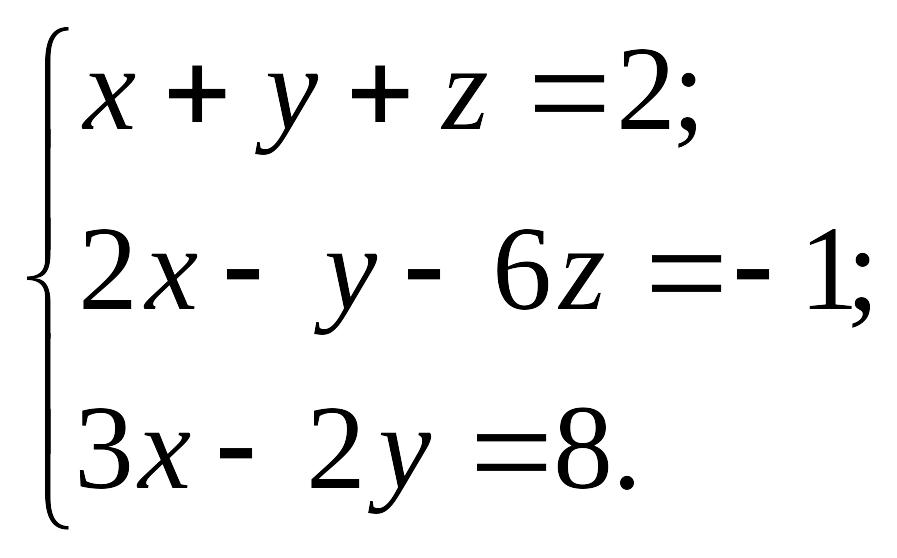
1.8.
1)
EMBED Equation.3
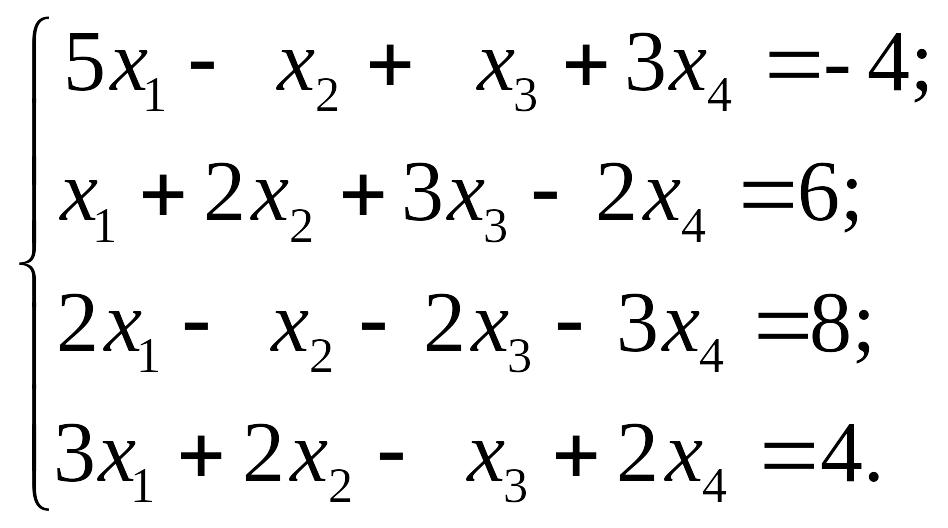 2)
EMBED Equation.3
2)
EMBED Equation.3
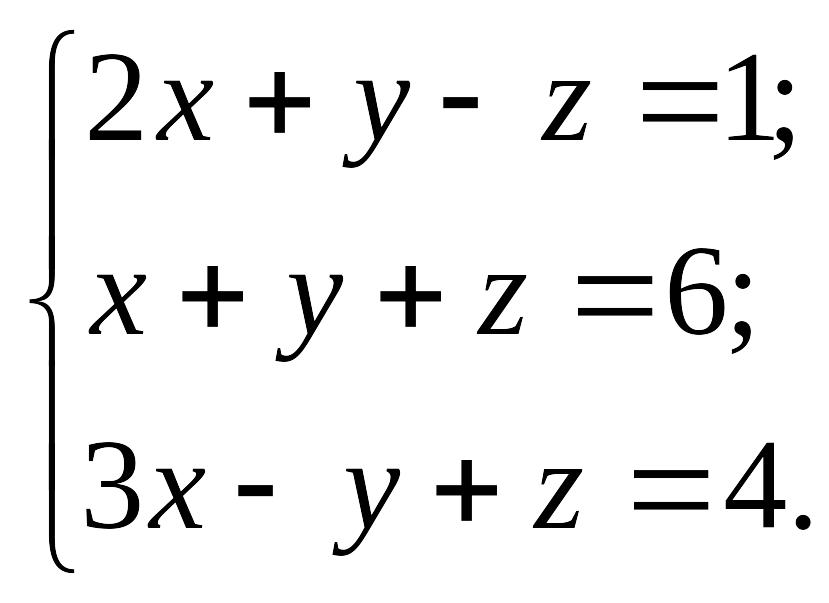
1.9.
1)
EMBED Equation.3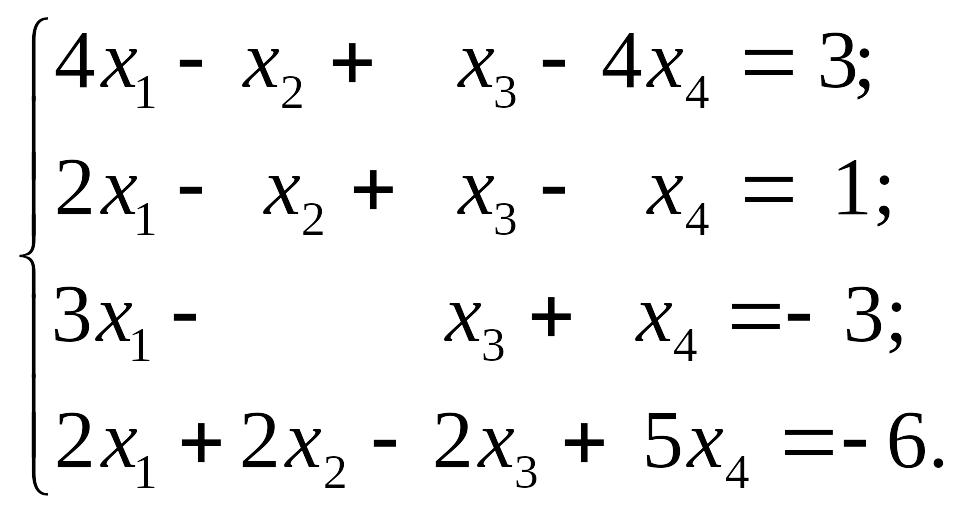 2) EMBED Equation.3
2) EMBED Equation.3
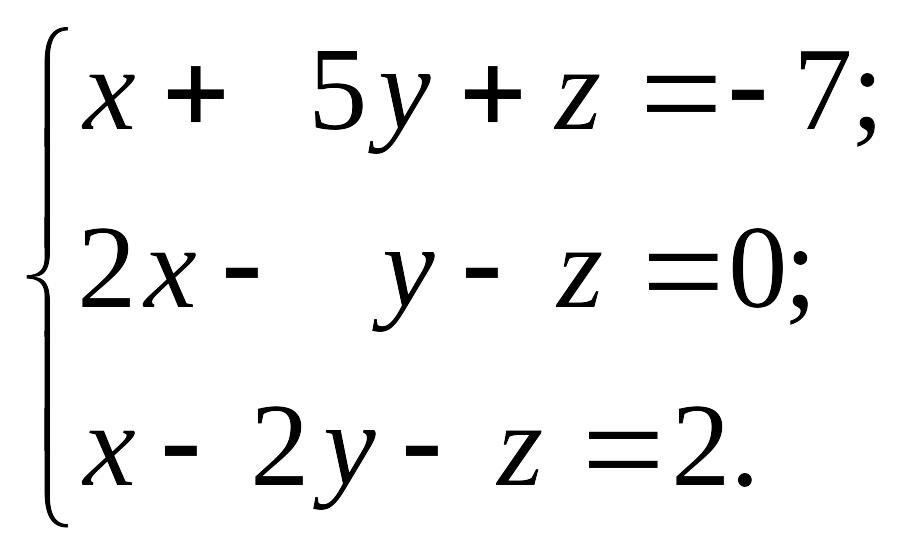
1.10
1)
EMBED Equation.3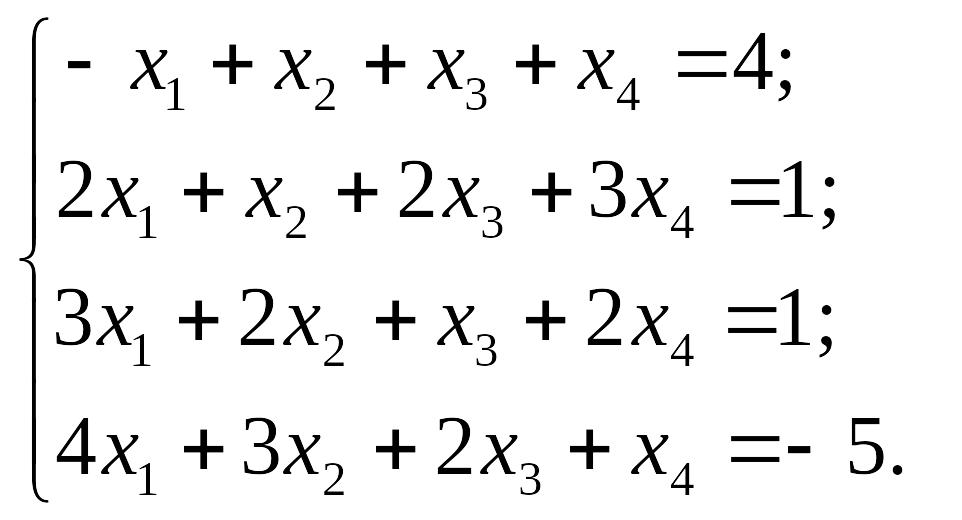 2) EMBED Equation.3
2) EMBED Equation.3
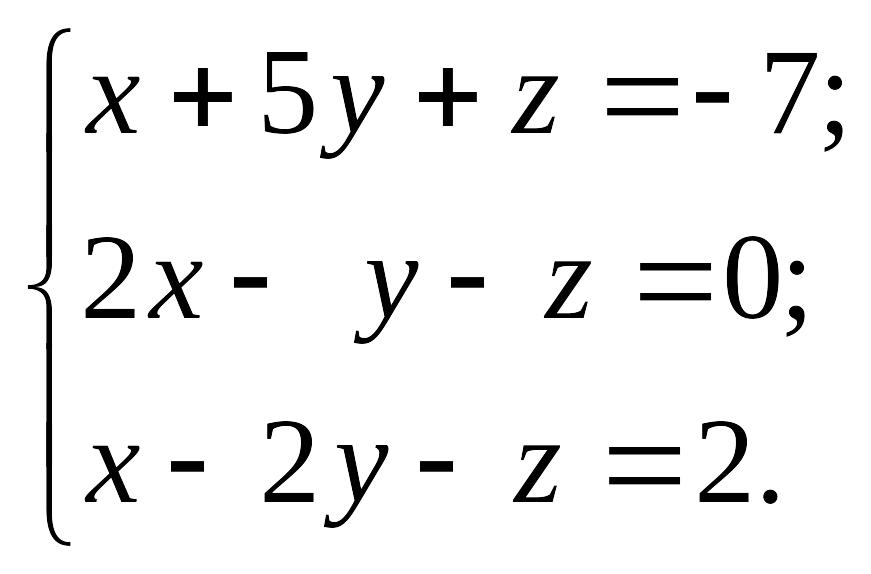
1.11.
1)
EMBED Equation.3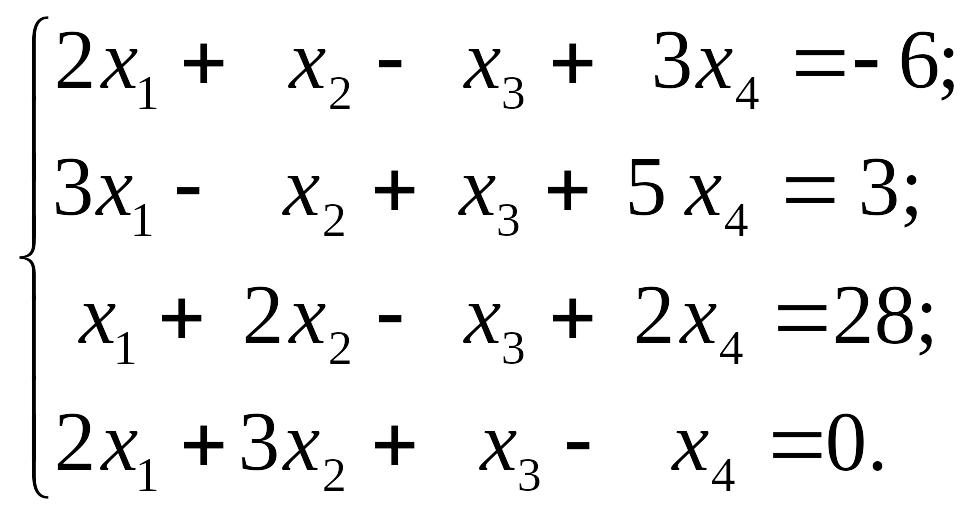 2) EMBED Equation.3
2) EMBED Equation.3
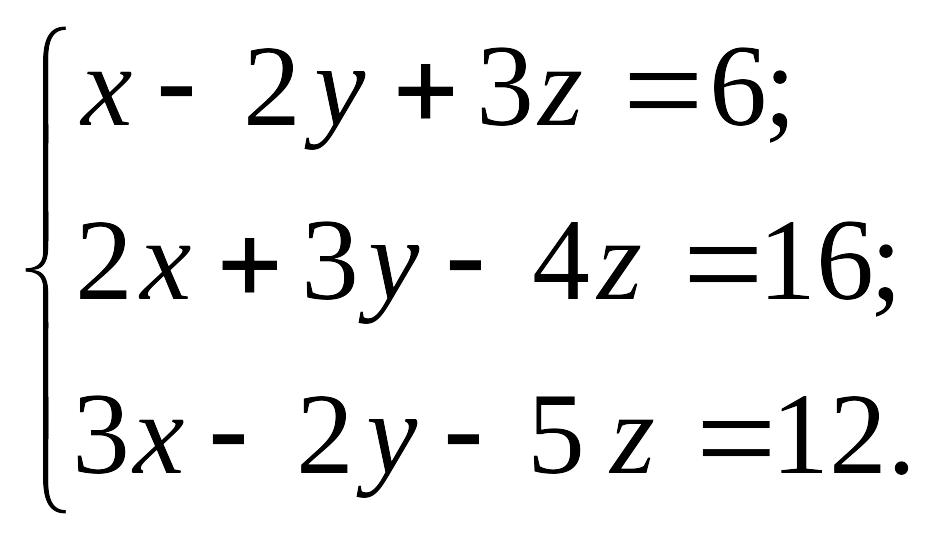
1.12.
1)
EMBED Equation.3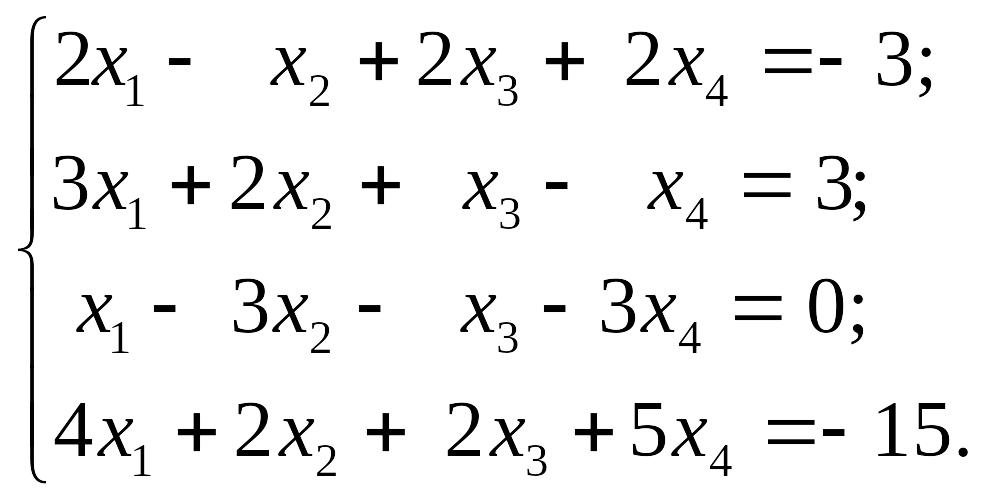 2) EMBED Equation.3
2) EMBED Equation.3
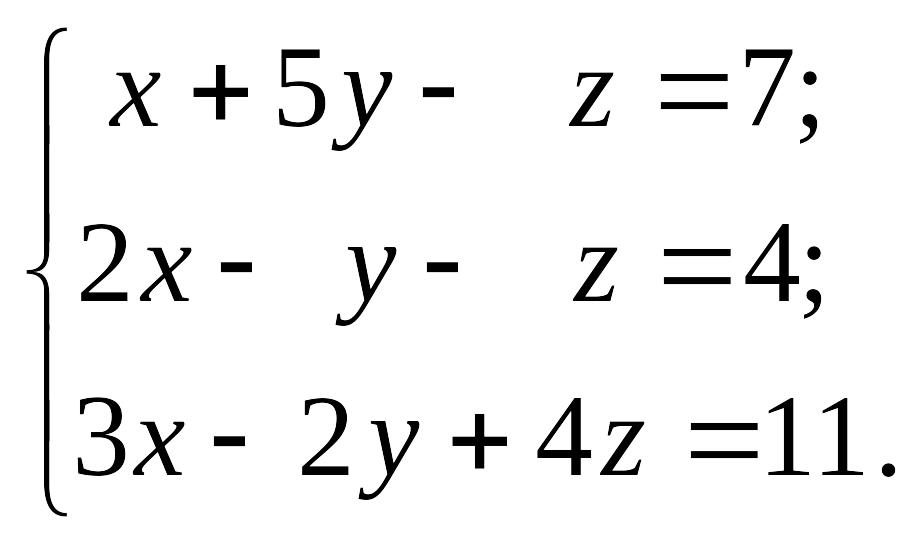
1.13.
1)
EMBED Equation.3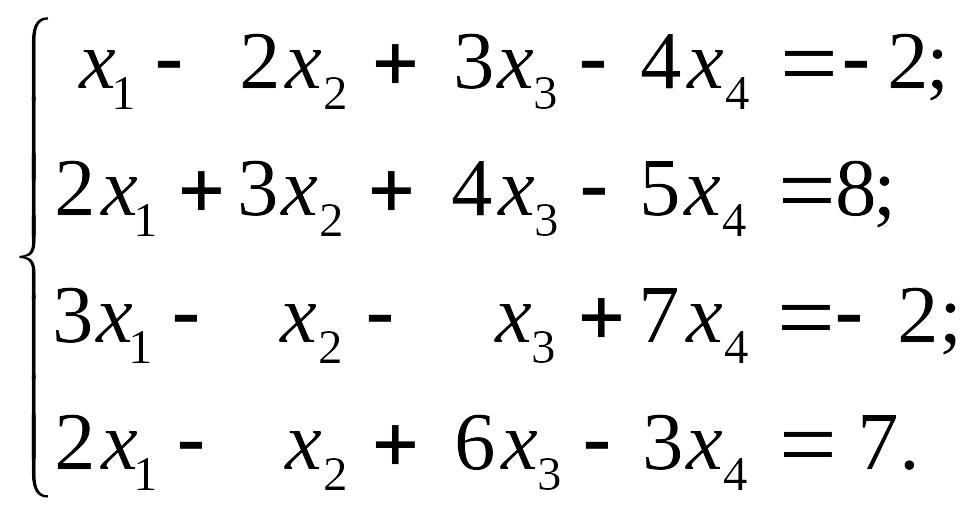 2) EMBED Equation.3
2) EMBED Equation.3
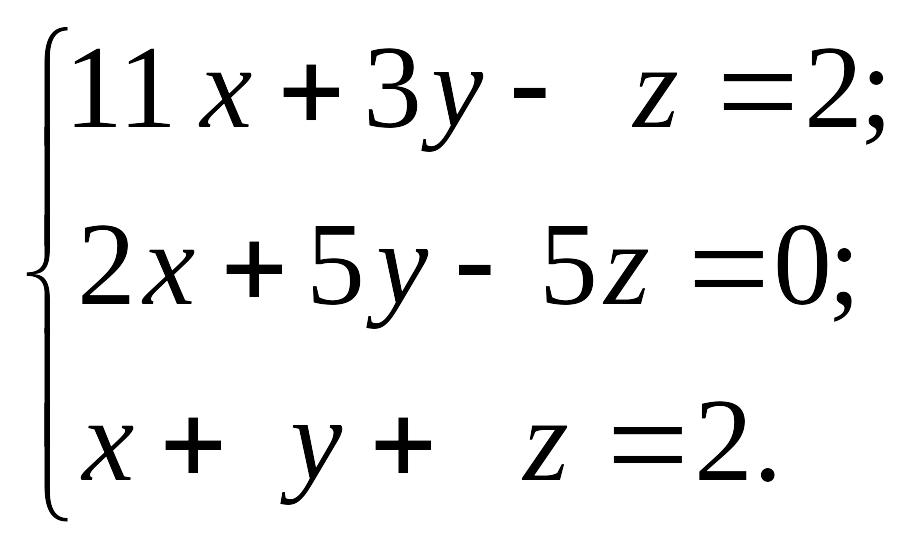
1.14.
1)
EMBED Equation.3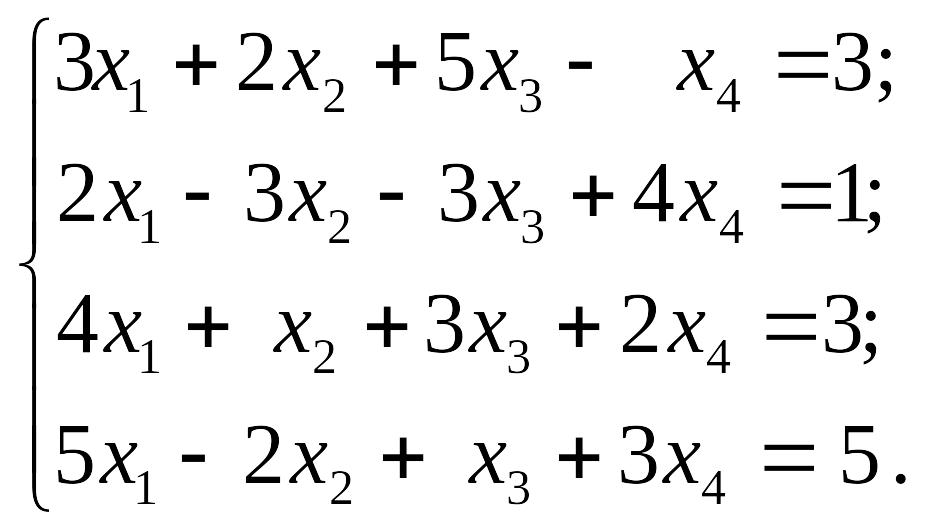 2) EMBED Equation.3
2) EMBED Equation.3
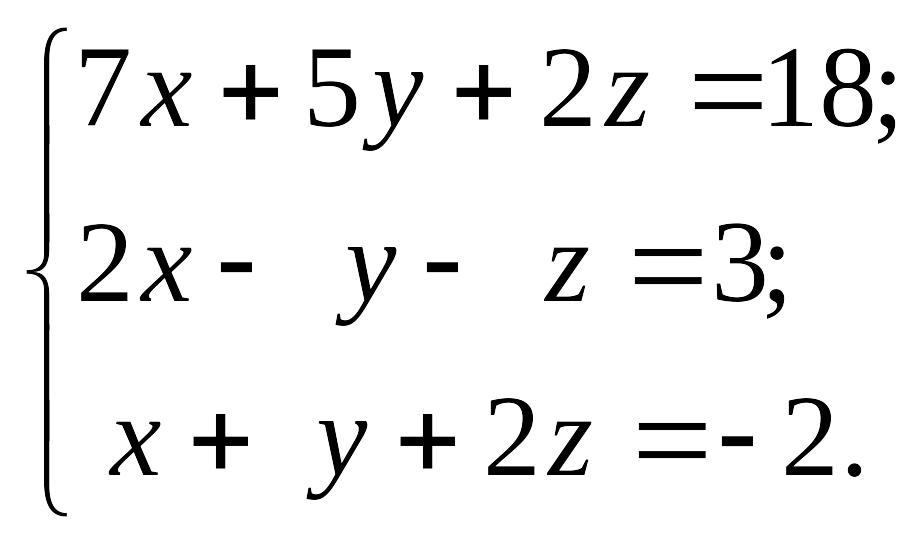
1.15.
1)
EMBED Equation.3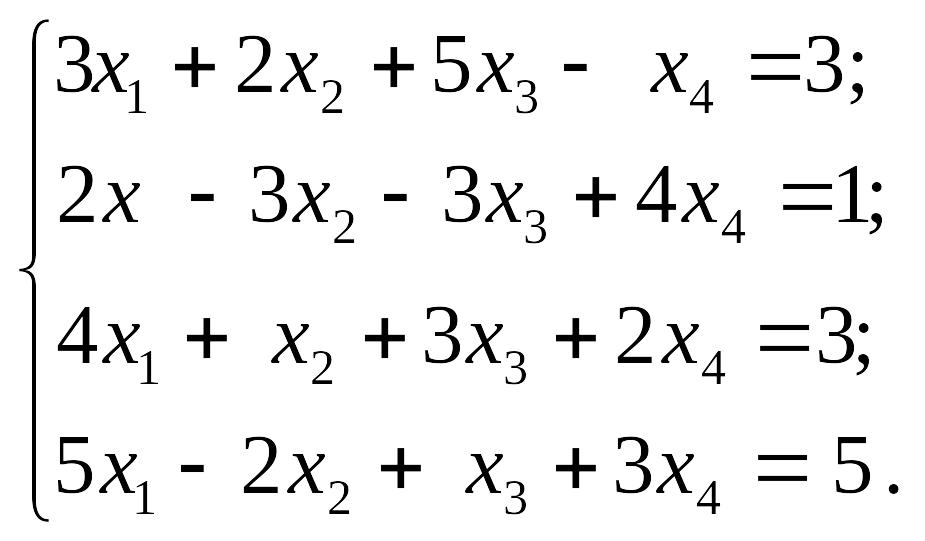 2) EMBED Equation.3
2) EMBED Equation.3
1.16.
1)
EMBED Equation.3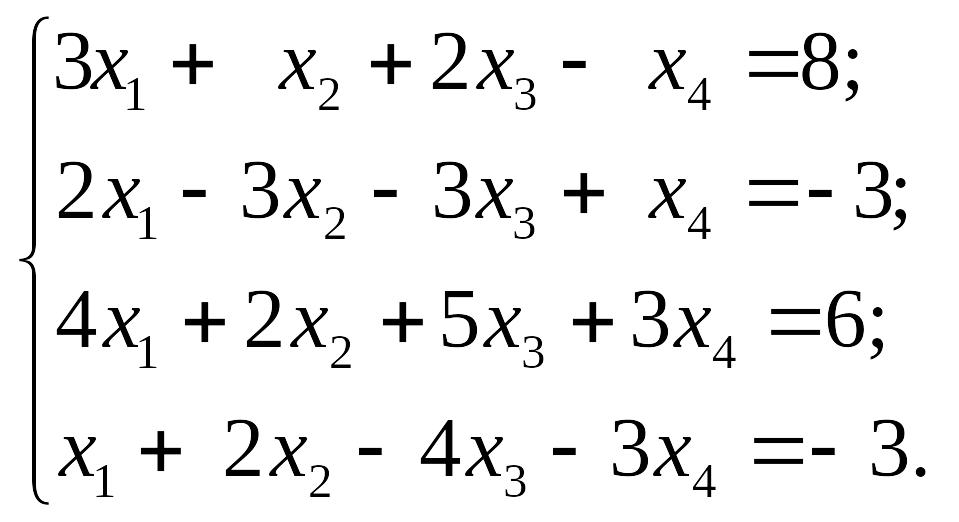 2) EMBED Equation.3
2) EMBED Equation.3
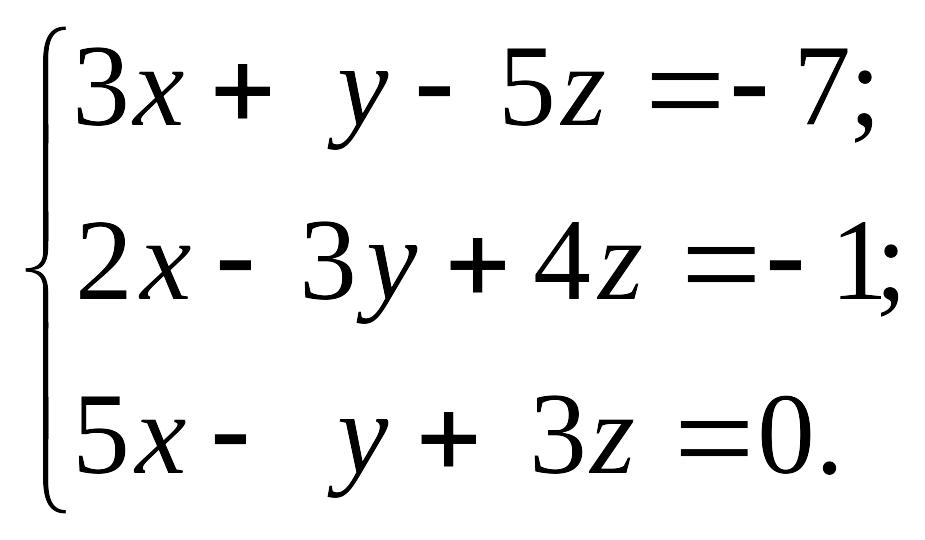
1.17.
1)
EMBED Equation.3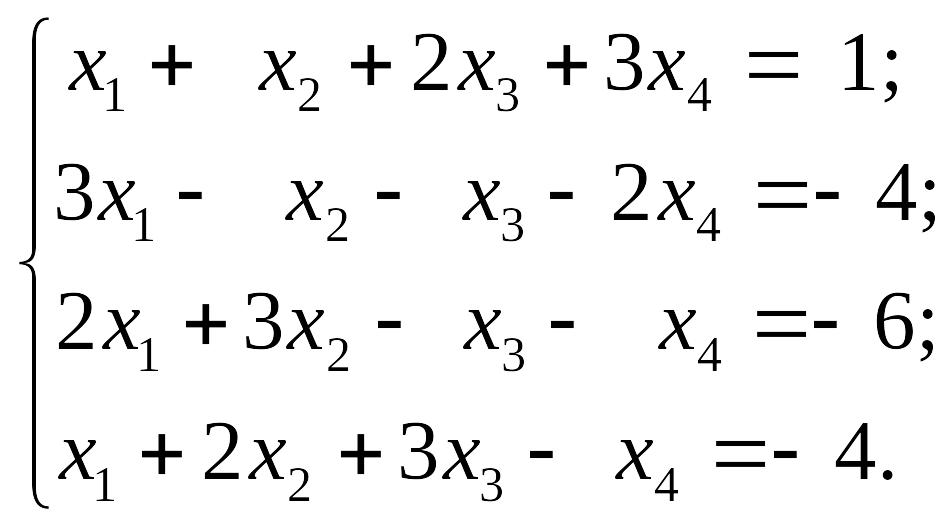 2) EMBED Equation.3
2) EMBED Equation.3
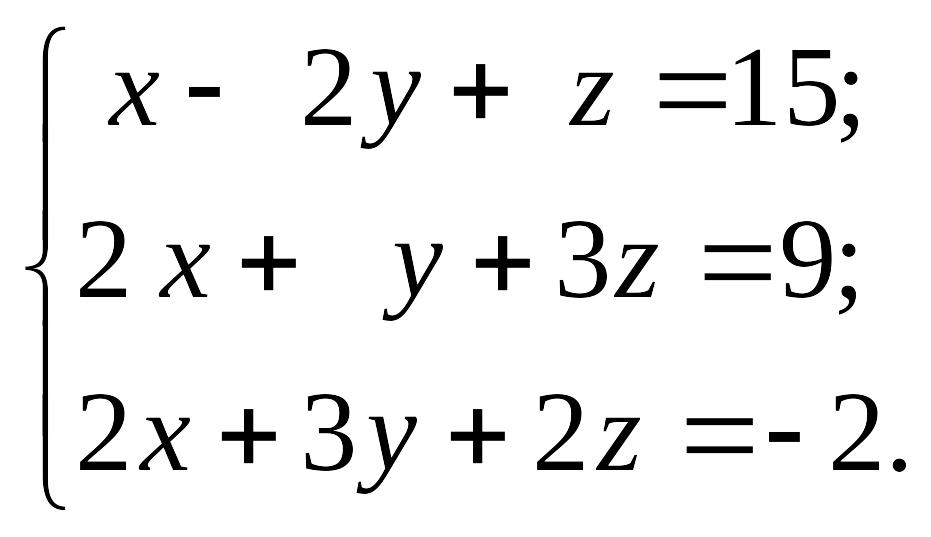
1.18.
1)
EMBED Equation.3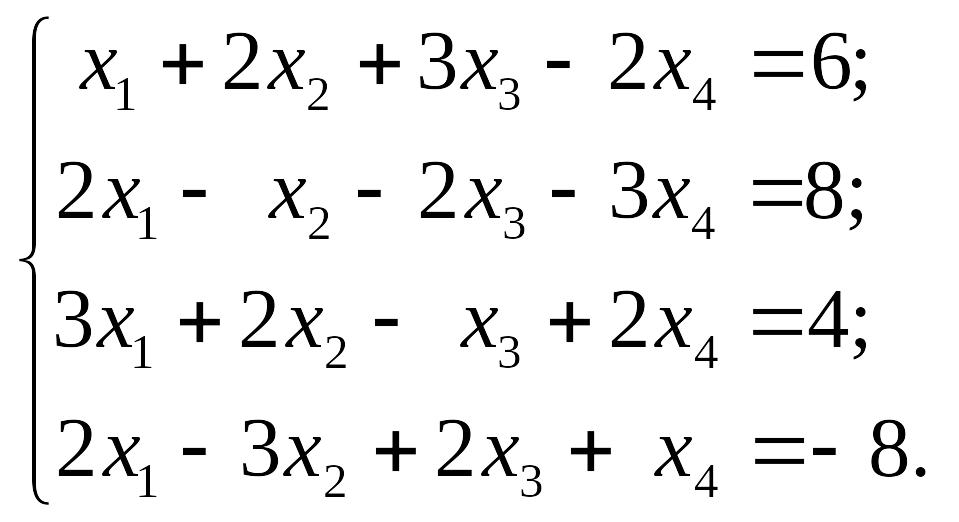 2) EMBED Equation.3
2) EMBED Equation.3
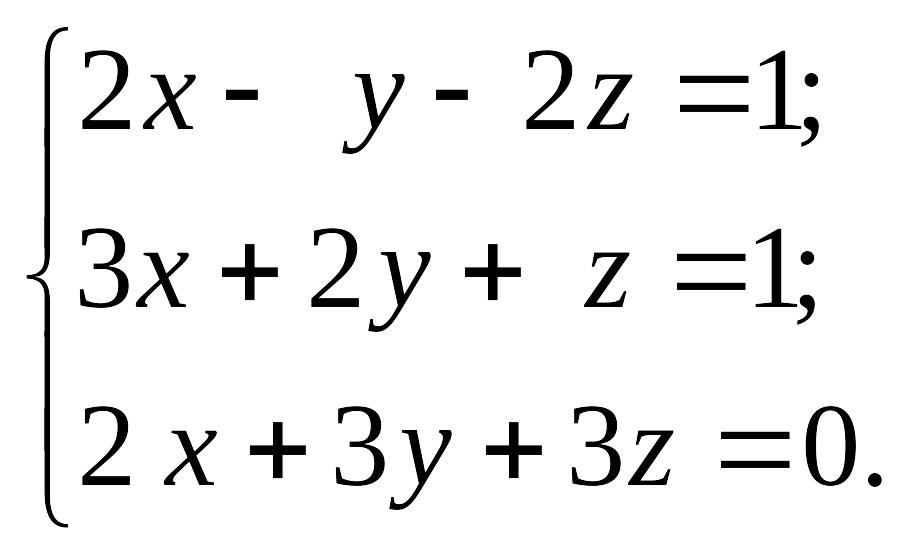
1.19.
1)
EMBED Equation.3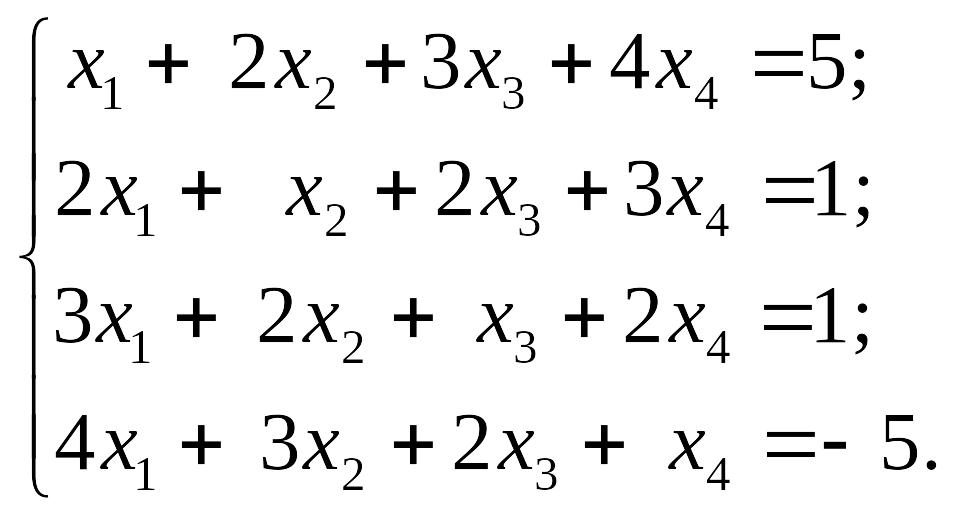 2) EMBED Equation.3
2) EMBED Equation.3
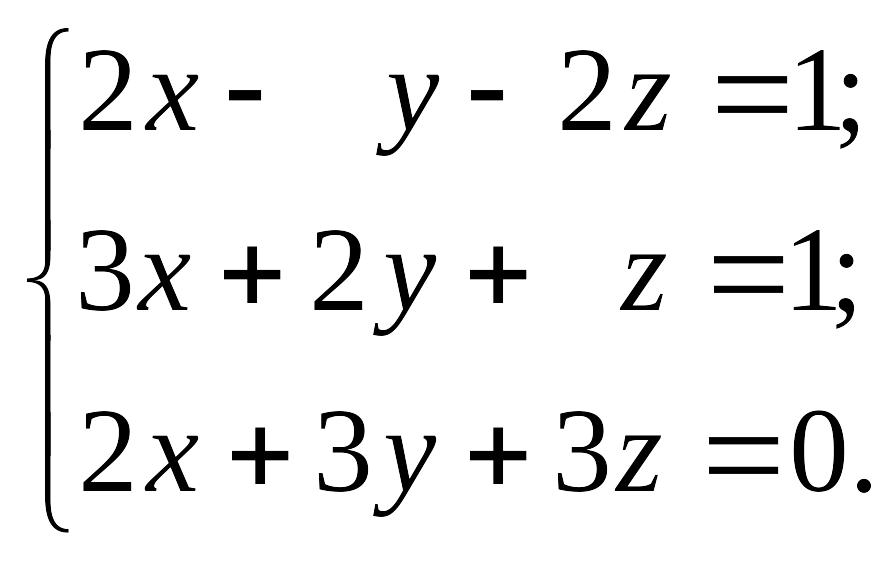
1.20.
1)
EMBED Equation.3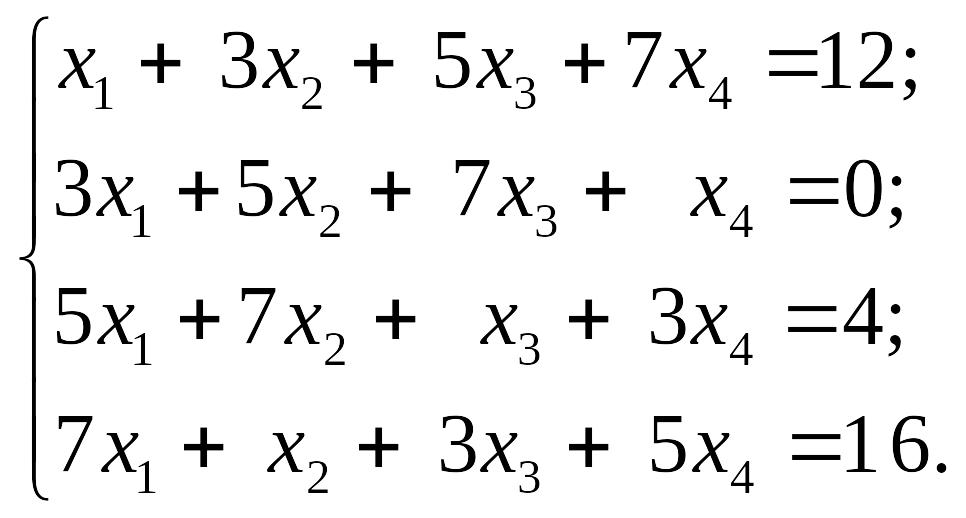 2) EMBED Equation.3
2) EMBED Equation.3
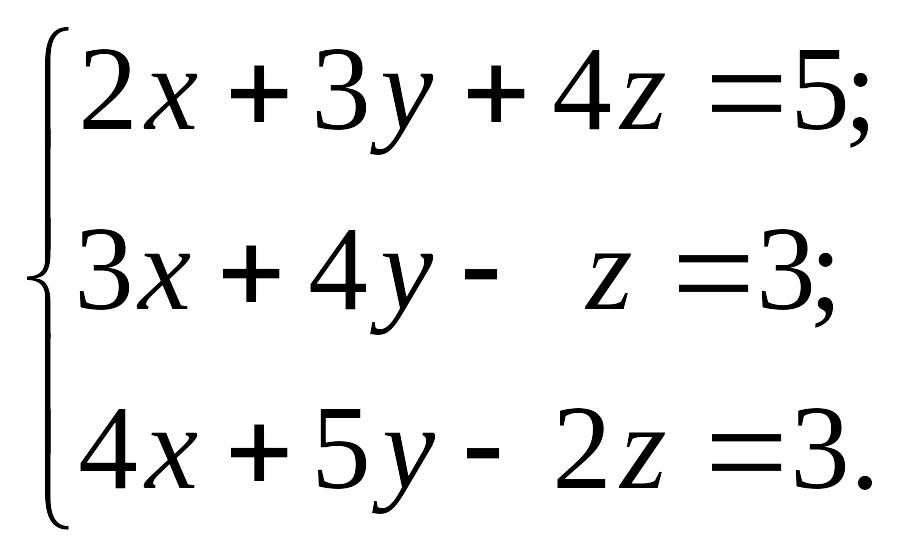
1.21.
1)
EMBED Equation.3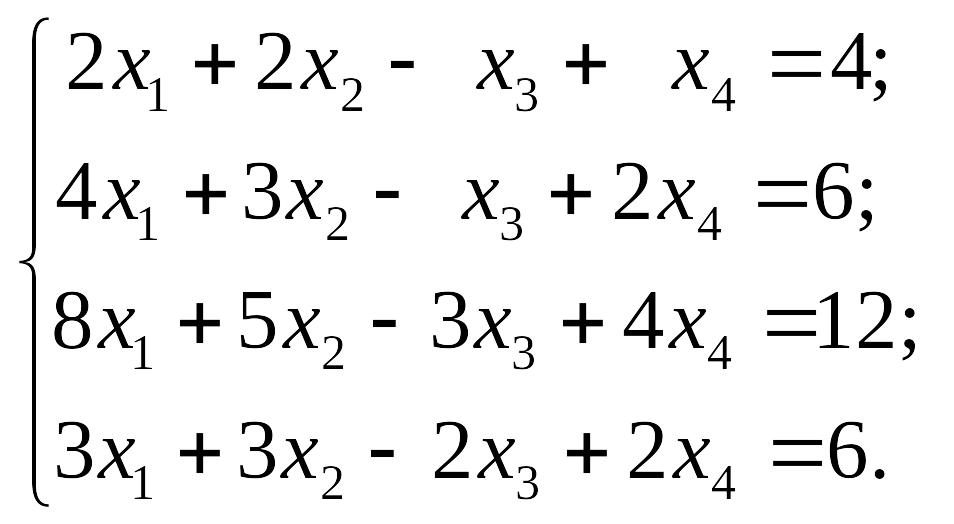 2) EMBED Equation.3
2) EMBED Equation.3
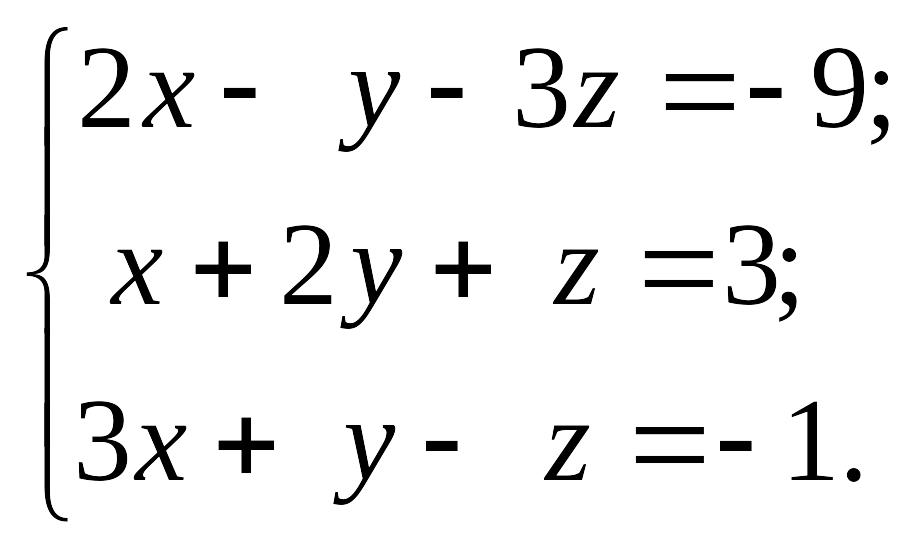
1.22.
1)
EMBED Equation.3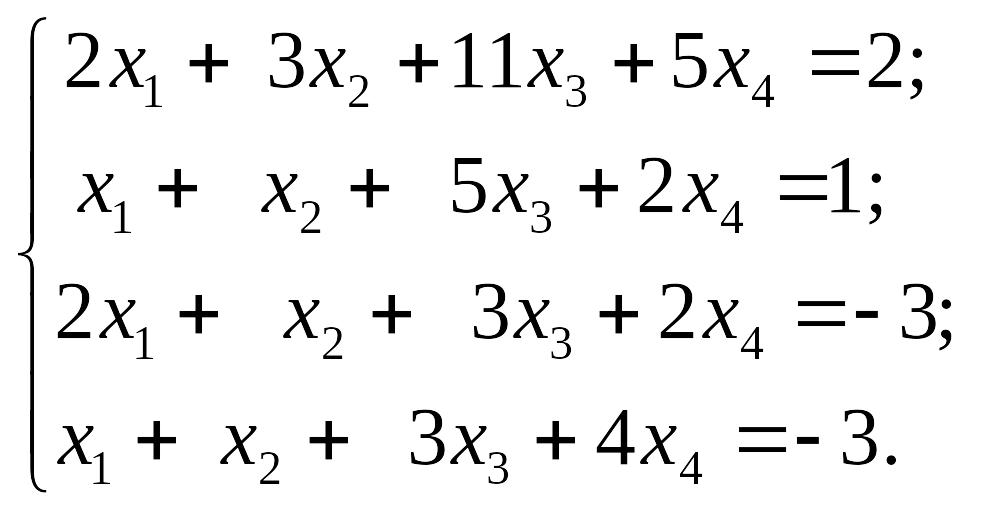 2) EMBED Equation.3
2) EMBED Equation.3
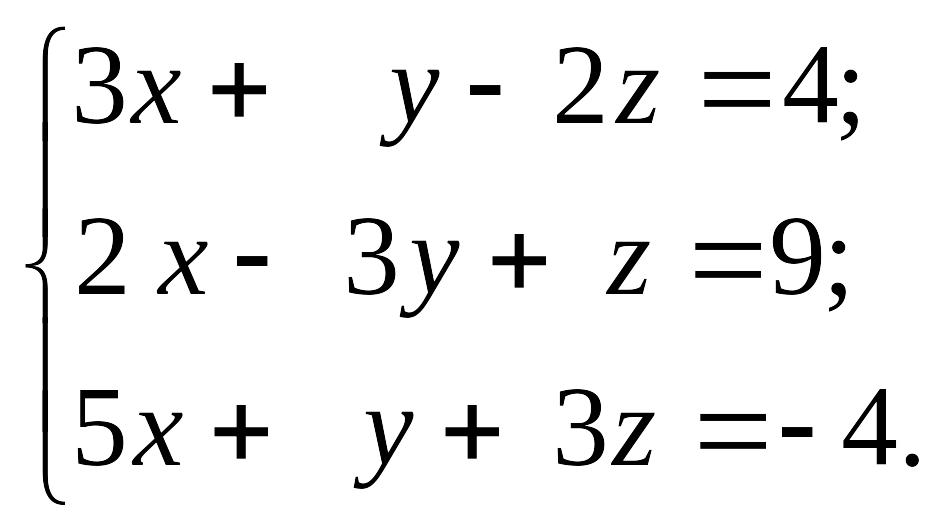
1.23
1)
EMBED Equation.3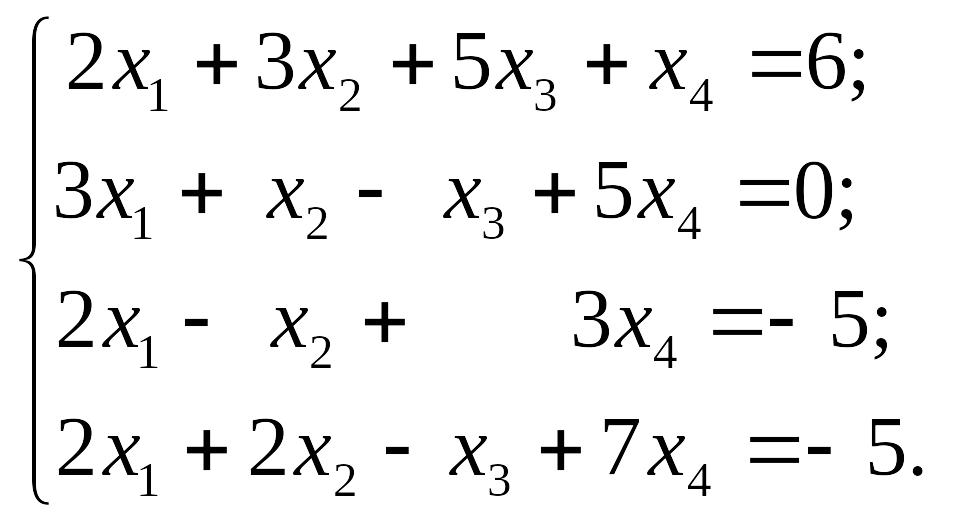 2) EMBED Equation.3
2) EMBED Equation.3
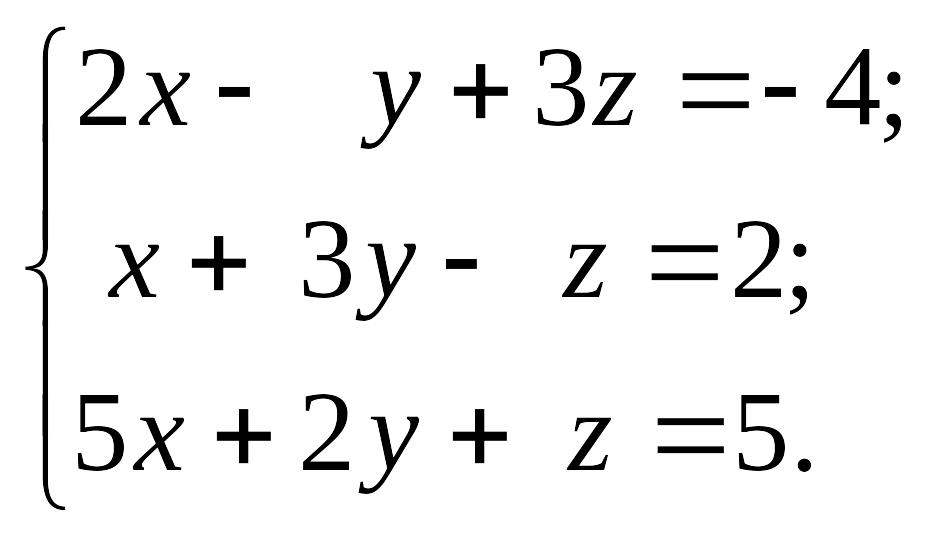
1.24.
1)
EMBED Equation.3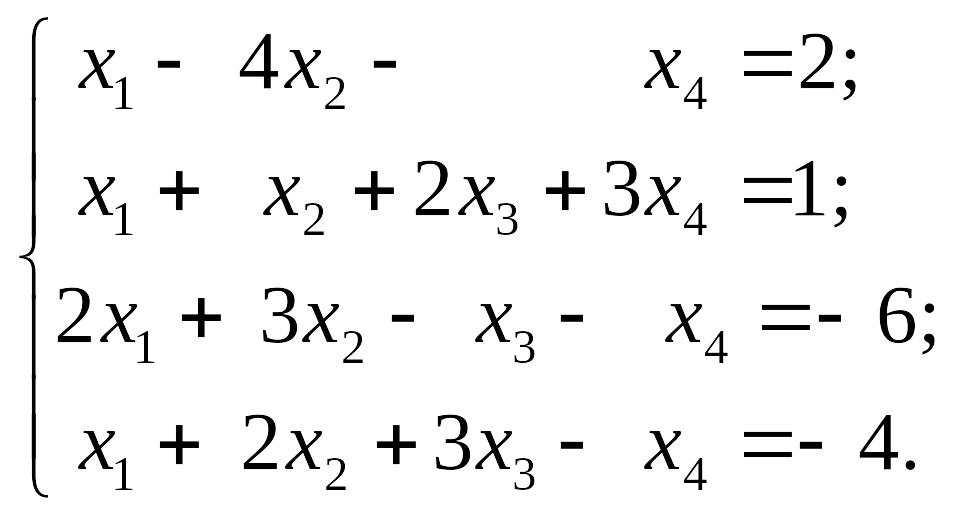 2) EMBED Equation.3
2) EMBED Equation.3
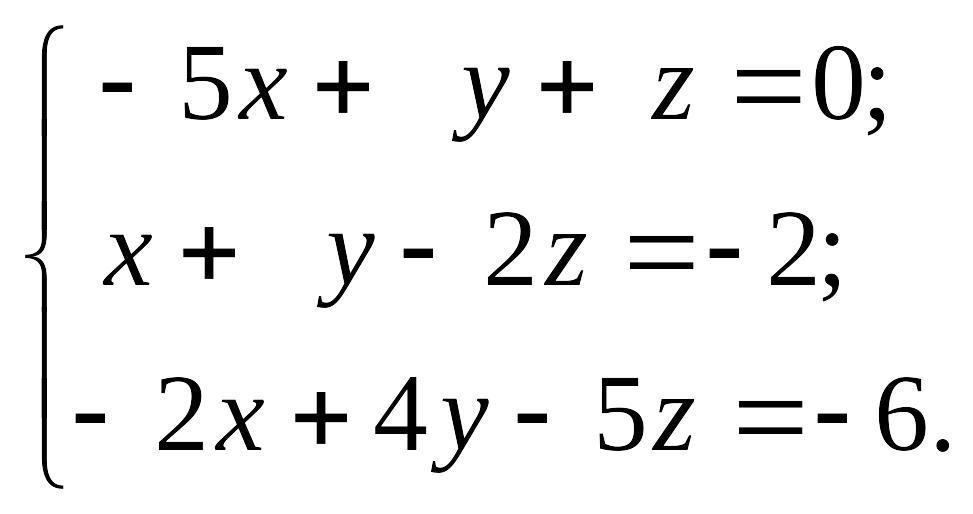
1.25.
1)
EMBED Equation.3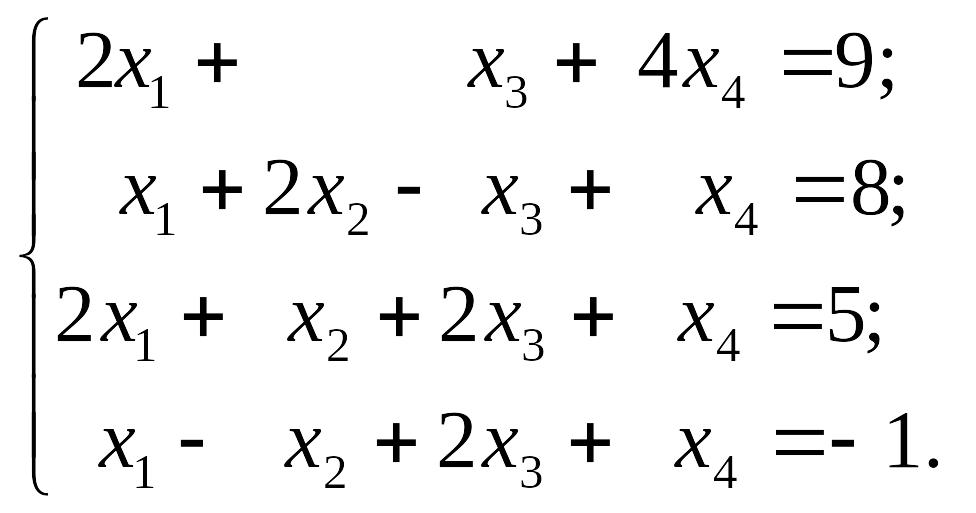 2) EMBED Equation.3
2) EMBED Equation.3
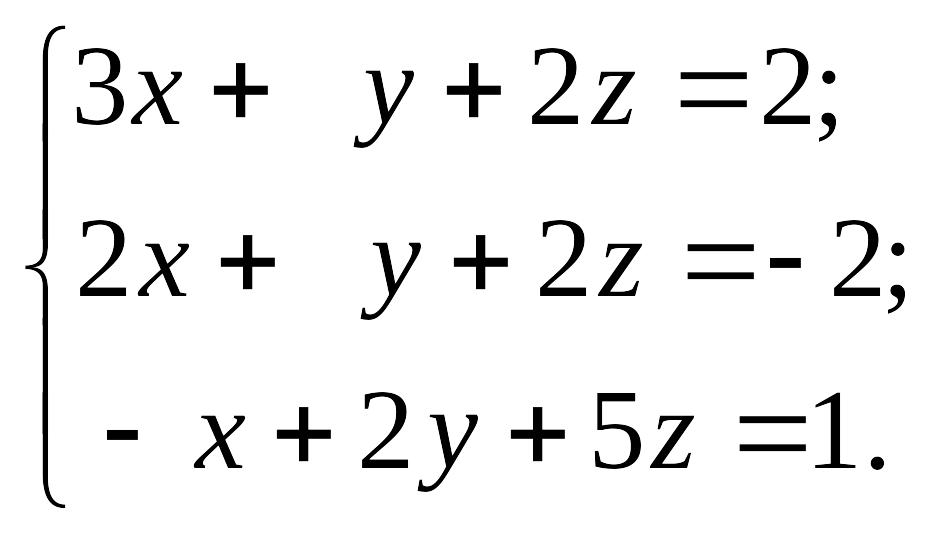
1.26.
1)
EMBED Equation.3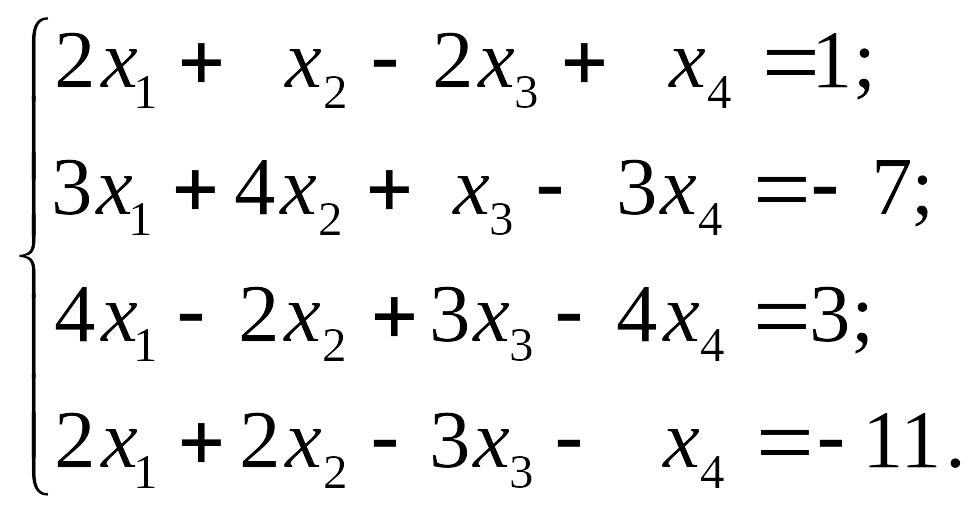 2) EMBED Equation.3
2) EMBED Equation.3
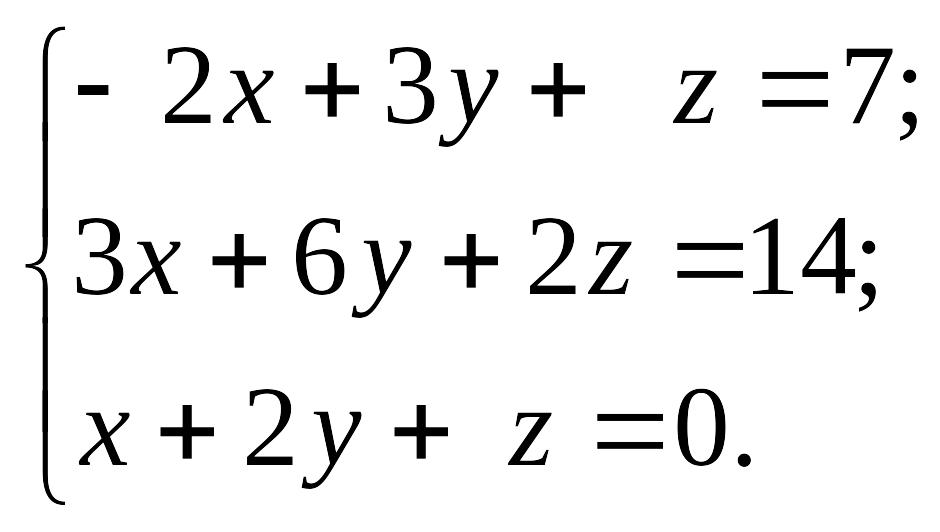
1.27.
1)
EMBED Equation.3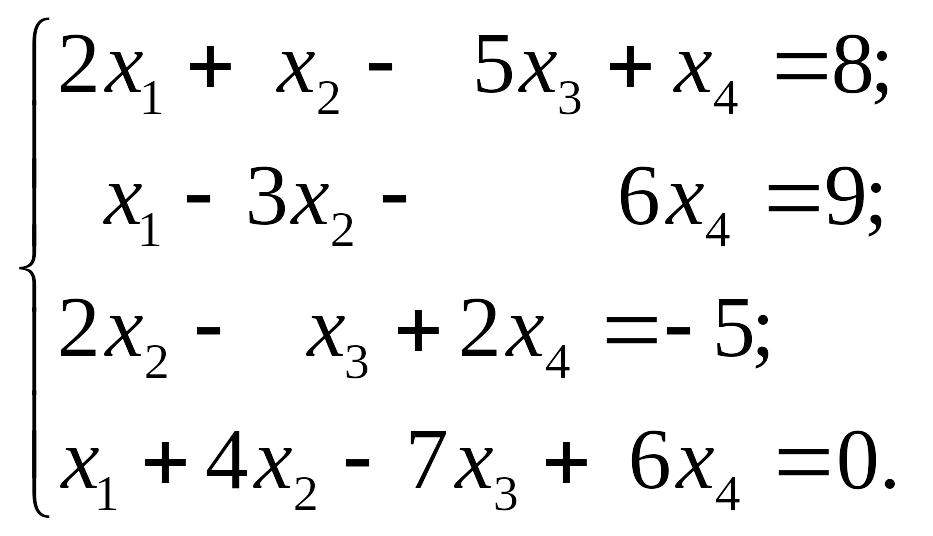 2) EMBED Equation.3
2) EMBED Equation.3
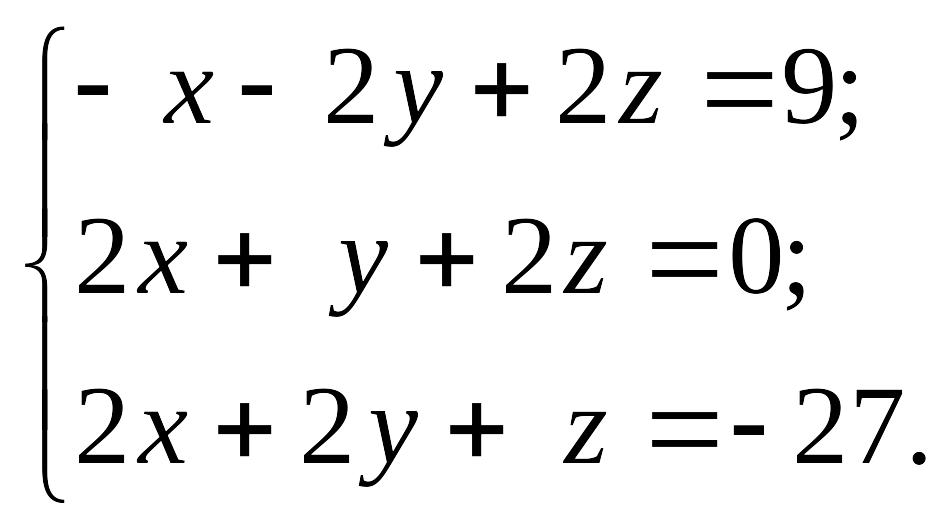
1.28.
1)
EMBED Equation.3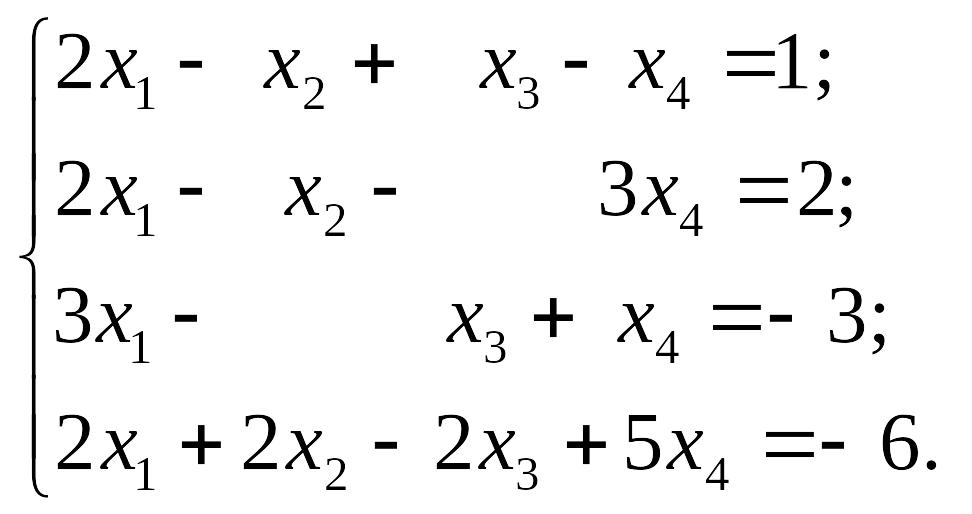 2) EMBED Equation.3
2) EMBED Equation.3
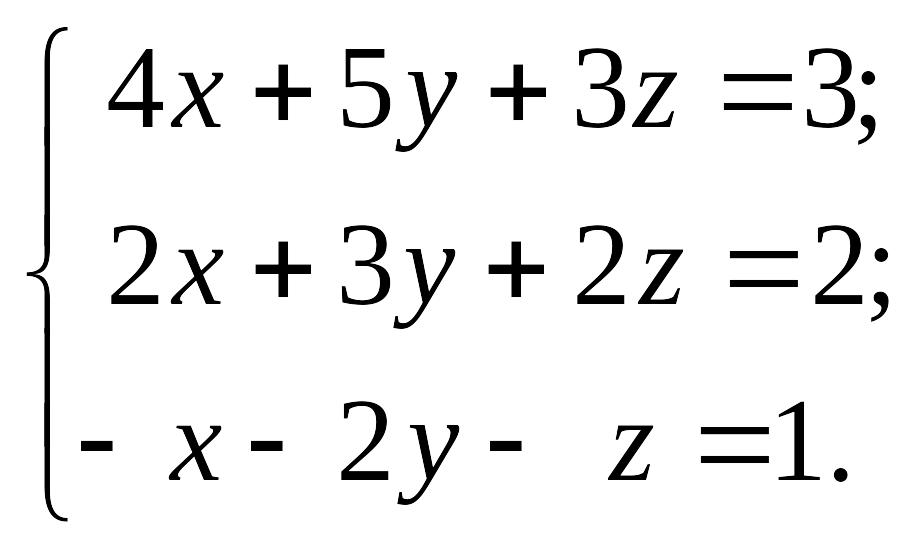
1.29.
1)
EMBED Equation.3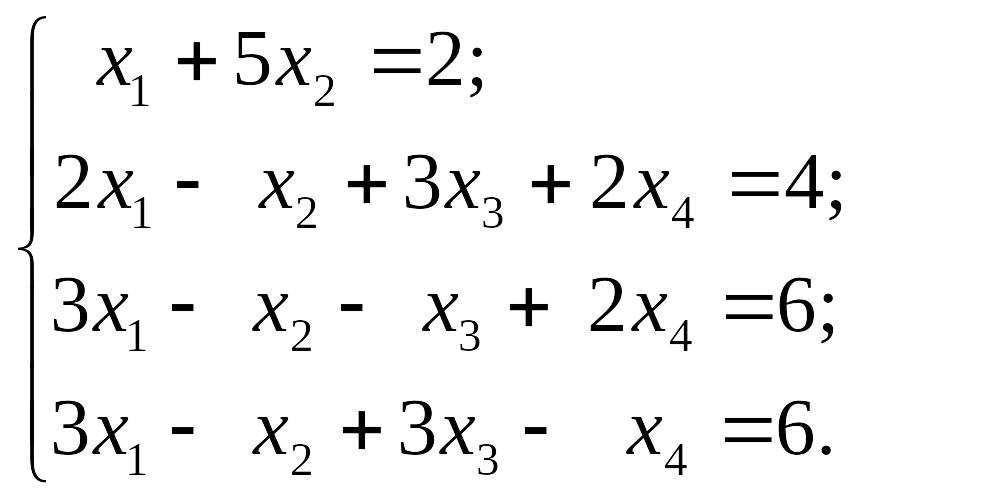 2) EMBED Equation.3
2) EMBED Equation.3
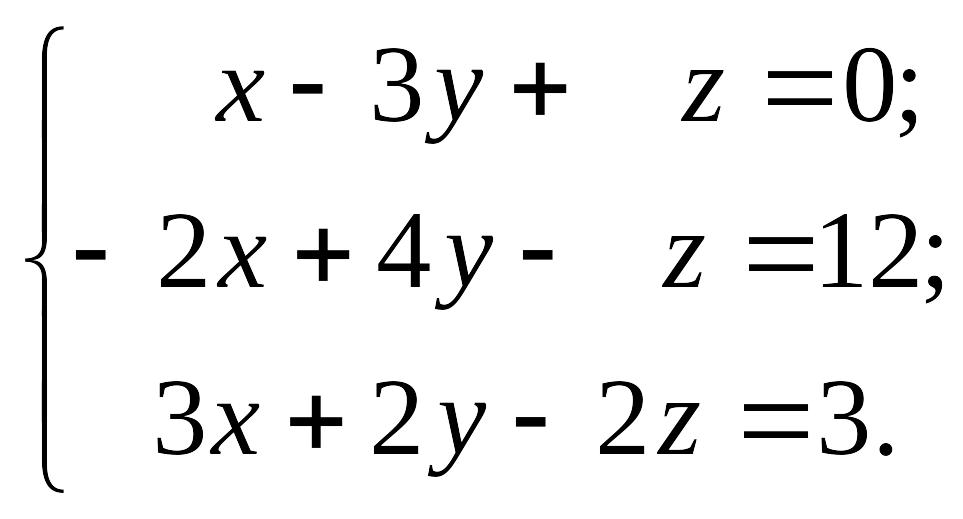
1.30.
1)
EMBED Equation.3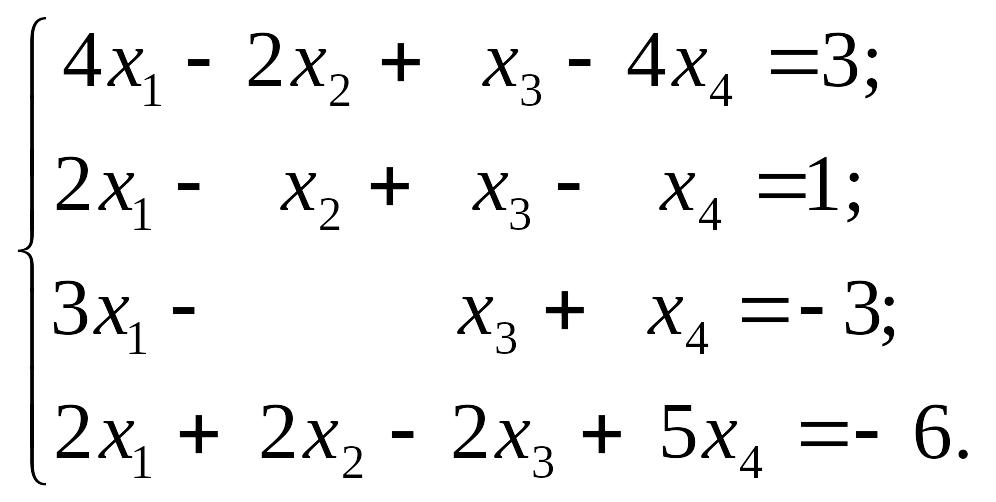 2) EMBED Equation.3
2) EMBED Equation.3
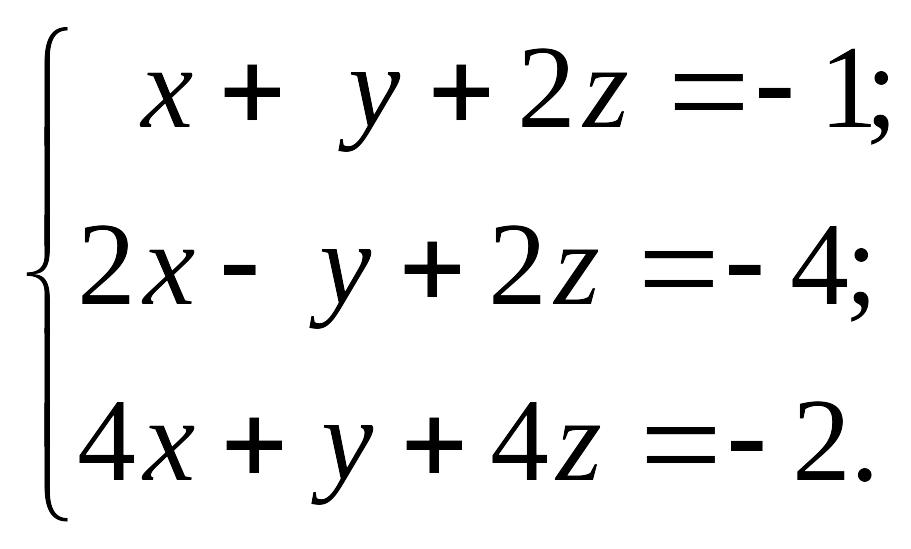
Задание 2. Найти значения матричного многочлена, если:
EMBED
Equation.3
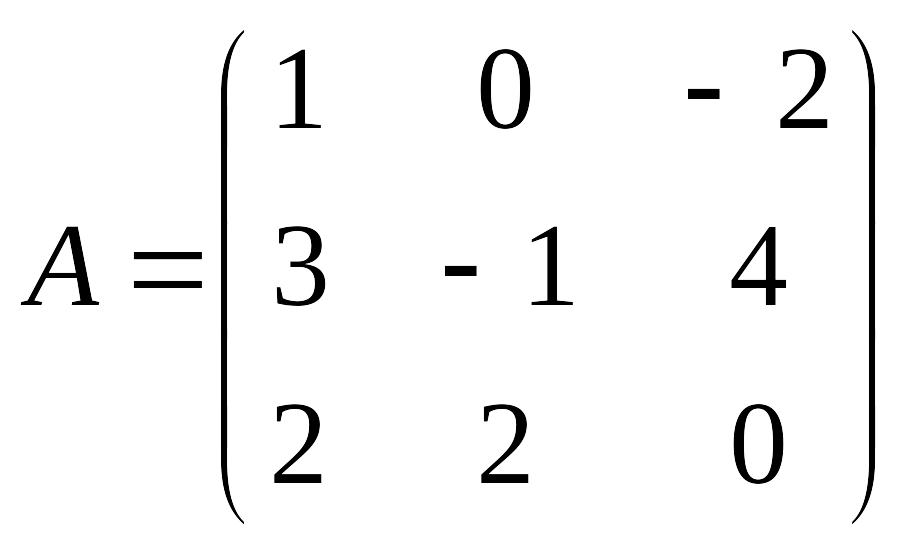 ;
EMBED Equation.3
;
EMBED Equation.3
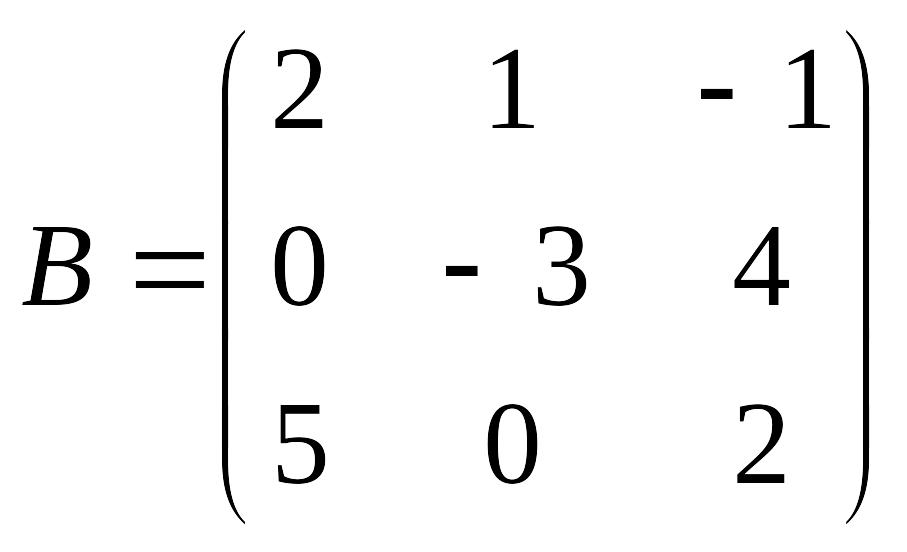 ;
;
EMBED
Equation.3
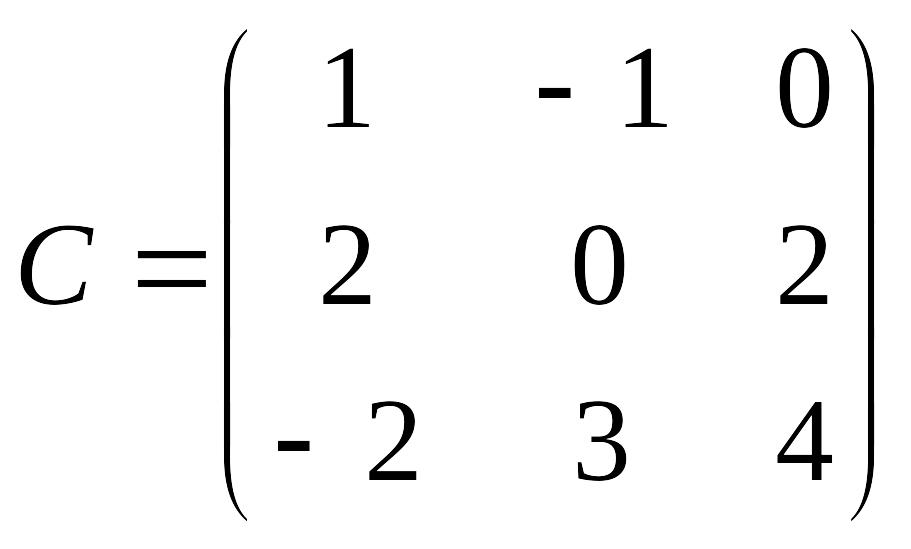 ;
EMBED Equation.3
;
EMBED Equation.3
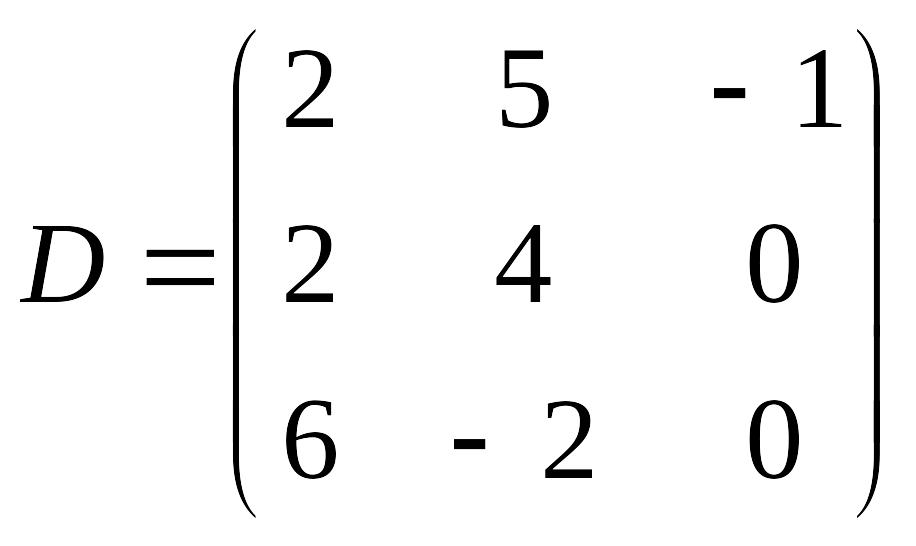 .
.
1.1.
EMBED Equation.3
![]() 1.16. EMBED Equation.3
1.16. EMBED Equation.3
![]()
1.2.
EMBED Equation.3
![]() 1.17. EMBED Equation.3
1.17. EMBED Equation.3
![]()
1.3.
EMBED Equation.3
![]() 1.18. EMBED Equation.3
1.18. EMBED Equation.3
![]()
1.4.
EMBED Equation.3
![]() 1.19. EMBED Equation.3
1.19. EMBED Equation.3
![]()
1.5.
EMBED Equation.3
![]() 1.20. EMBED Equation.3
1.20. EMBED Equation.3
![]()
1.6.
EMBED Equation.3
![]() 1.21. EMBED Equation.3
1.21. EMBED Equation.3
![]()
1.7.
EMBED Equation.3
![]() 1.22. EMBED Equation.3
1.22. EMBED Equation.3
![]()
1.8.
EMBED Equation.3
![]() 1.23. EMBED Equation.3
1.23. EMBED Equation.3
![]()
1.9.
EMBED Equation.3
![]() 1.24. EMBED Equation.3
1.24. EMBED Equation.3
![]()
1.10.
EMBED Equation.3
![]() 1.25. EMBED Equation.3
1.25. EMBED Equation.3
![]()
1.11.
EMBED Equation.3
![]() 1.26. EMBED Equation.3
1.26. EMBED Equation.3
![]()
1.12.
EMBED Equation.3
![]() 1.27. EMBED Equation.3
1.27. EMBED Equation.3
![]()
1.13.
EMBED Equation.3
![]() 1.28. EMBED Equation.3
1.28. EMBED Equation.3
![]()
1.14.
EMBED Equation.3
![]() 1.29. EMBED Equation.3
1.29. EMBED Equation.3
![]()
1.15.
EMBED Equation.3
![]()
1.30. EMBED Equation.3
1.30. EMBED Equation.3
![]()
