
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
Пусть две плоскости заданы общими уравнениями.
А1х + В1у + С1z +D1 = 0
А2х + В2у + С2z + D2 = 0
Вопрос об определении угла между ними сводится к определению угла между их нормальными векторами
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() .
(Две пересекающиеся плоскости образуют
два угла, в сумме равные p.
Нам достаточно определить один из
углов).
.
(Две пересекающиеся плоскости образуют
два угла, в сумме равные p.
Нам достаточно определить один из
углов).
Тогда ,используя формулу для косинуса угла между векторами, имеем
EMBED Equation.3
![]() (11.3)
(11.3)
-угол между двумя плоскостями.
Условие
параллельности плоскостей
эквивалентно условию коллинеарности
векторов EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() имеет вид :
имеет вид :
EMBED
Equation.3
![]() (11.4)
(11.4)
и
заключается в пропорциональности
координат этих векторов. Если EMBED
Equation.3
![]() ,
то плоскости совпадают.
,
то плоскости совпадают.
Условие перпендикулярности плоскостей вытекает из формулы (2.3), когда cosj = 0 или ( EMBED Equation.3 , EMBED Equation.3 ) = 0, т.е.
EMBED Equation.3
![]() .
(11.5)
.
(11.5)
Пример 11.1.
Определить отрезки, отсекаемые
плоскостью EMBED Equation.3
![]() на осях координат.
на осях координат.
Решение. Переписав
уравнение в виде EMBED Equation.3
![]() ,
,
и, разделив обе части его на 4, получим
EMBED Equation.3
![]() или EMBED Equation.3
или EMBED Equation.3
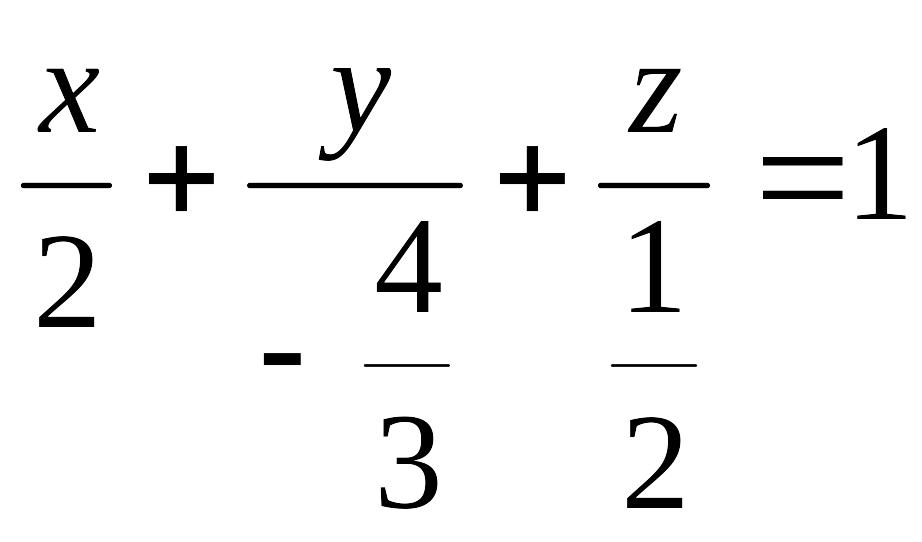 .
.
Получили уравнение
плоскости в отрезках. Откуда EMBED
Equation.3
![]() - отрезки, отсекаемые плоскостью от осей
координат EMBED Equation.3
- отрезки, отсекаемые плоскостью от осей
координат EMBED Equation.3
![]() ,
соответственно.
,
соответственно.
Пример 11.2.. Из точки Р (2; 3; —5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение.
Основаниями
перпендикуляров, опущенных на координатные
плоскости, будут следующие точки: EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() Запишем уравнение плоскости, проходящей
через точки EMBED Equation.3
Запишем уравнение плоскости, проходящей
через точки EMBED Equation.3
![]() ,
для чего воспользуемся уравнением
,
для чего воспользуемся уравнением
EMBED
Equation.3
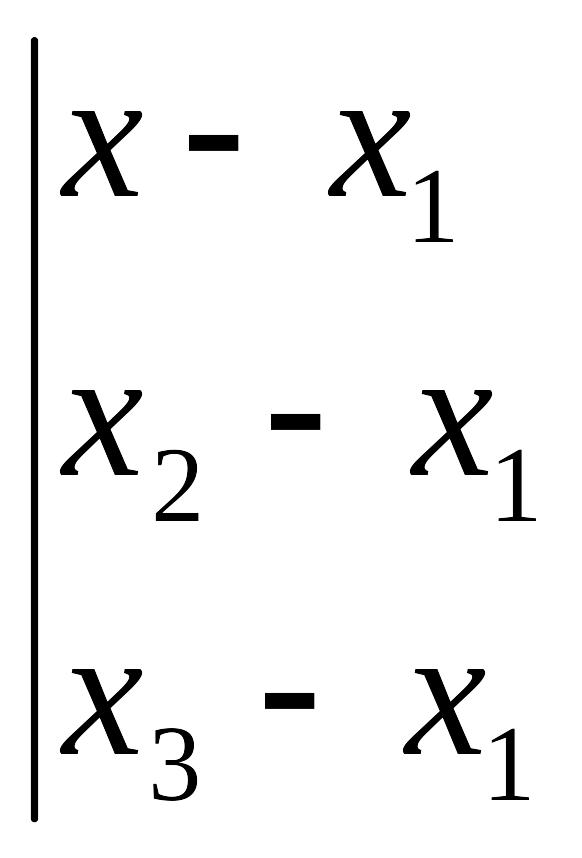 EMBED
Equation.3
EMBED
Equation.3
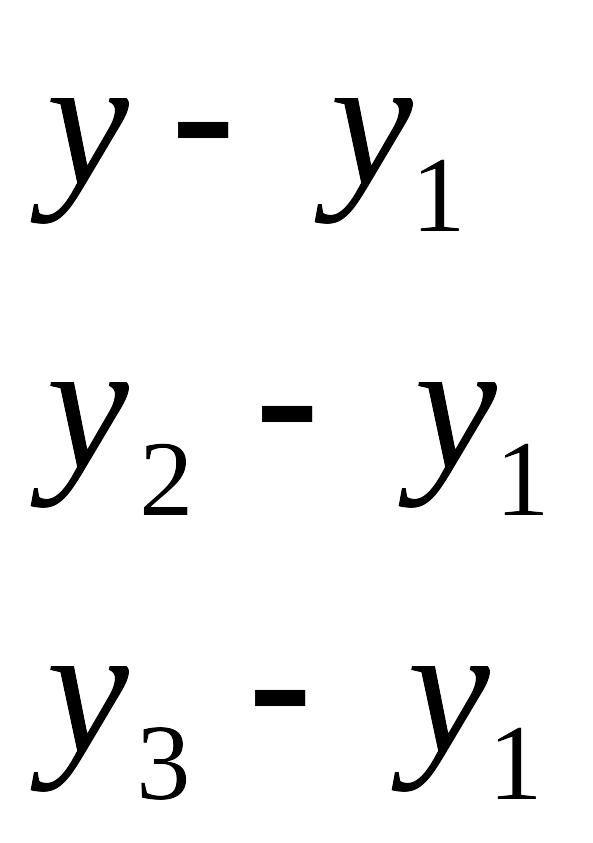 EMBED
Equation.3
EMBED
Equation.3
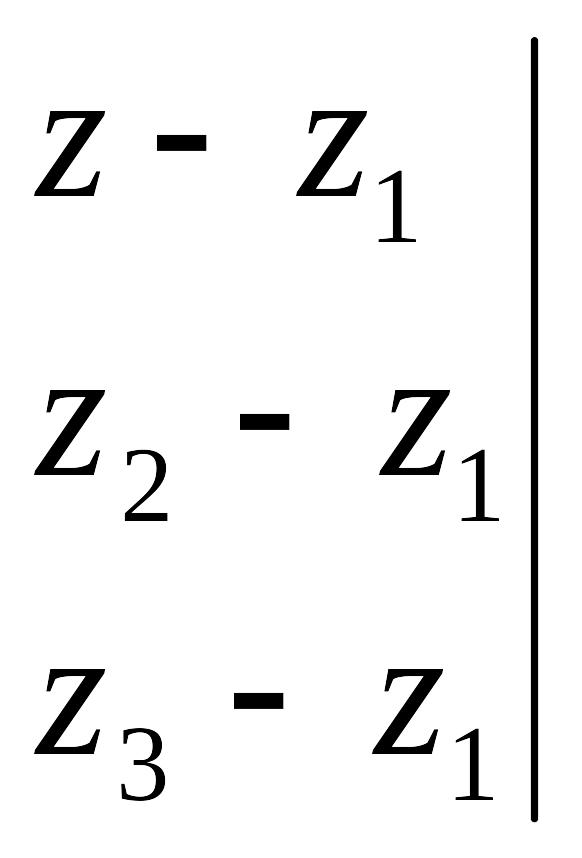 =0,
=0,
находим
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]() =0
или 15x+10y-6z-60=0.
=0
или 15x+10y-6z-60=0.
Пример 11.3. Определить, при каких значениях l и m следующие уравнения будут определять параллельные плоскости.
2x+ ly+3z -5=0, mx-6y - 6z +2=0.
Решение. Если плоскости параллельны, то их нормальные векторы также параллельны.
Имеем.
EMBED
Equation.DSMT4
![]() .
Из условия
параллельности векторов находим
.
Из условия
параллельности векторов находим
EMBED Equation.DSMT4
![]() .
Следовательно, l
=3,
m
= - 4.
.
Следовательно, l
=3,
m
= - 4.
Пример 11.4. Определить, при каком значении l следующие уравнения будут определять перпендикулярные плоскости.
3x - 5y+ lz -3=0, x + 3y+ 2z +5=0.
Решение. Если плоскости перпендикулярны, то их нормальные векторы также перпендикулярны.
Имеем.
EMBED Equation.DSMT4
![]() .
Векторы
будут перпендикулярны, если
EMBED Equation.DSMT4
.
Векторы
будут перпендикулярны, если
EMBED Equation.DSMT4
![]()
EMBED
Equation.DSMT4
![]() Откуда
l
=6.
Откуда
l
=6.
Пример 11.5. Определить, двугранный угол, образованный пересечением плоскостей:
6x + 3y - 2z =0, x + 2y+ 6z - 12=0.
Решение. Двугранный угол между плоскостями равен углу между их нормальными векторами.
Имеем.
EMBED Equation.DSMT4
![]() .
.
Воспользуемся формулой (2.3)
EMBED Equation.3
![]()
Следовательно, искомый угол π / 2
.Вопросы для самопроверки
Как записывается уравнение плоскости в отрезках?
Как записывается уравнение плоскости, проходящей через три заданные точки?
Как вычисляется угол между двумя плоскостями?
Каковы условия параллельности и перпендикулярности двух плоскостей?
