§ 2. Интервальные оценки

1. Доверительные интервалы. Недостаток точечных оценок состоит в том, что неизвестно, с какой точностью они приближают оцениваемый параметр. Если для большого числа наблюдений точность обычно бывает достаточной для практических выводов, то для выборок небольшого объема вопрос о точности является существенным. Этот вопрос решается с помощью так называемой интервальной оценки. Именно, для неизвестного параметра  подбирается интервал так, чтобы с большой вероятностью выполнялось соотношение . На практике ₁ и ₂ определяются выборкой значений случайной величины, т. е. ₁  ₁(x₁, x₂, ..., x_n), ₂  ₂(x₁, x₂, ..., x_n), а значит, являются случайными величинами. Отсюда следует, что есть событие, имеющее определенную вероятность.

Определение. Пусть 0 <  < 1. Если выполняется неравенство l , то и называют доверительными границами, а сам интервал – доверительным интервалом для параметра  с надежностью .

Надежность  интервальной оценки в соответствии с практической задачей принято выбирать в пределах от 0,95 до 0,999. Тогда вероятность того, что данный параметр не попадет в доверительный интервал, находится в пределах от 0,001 до 0,05. Если считать такое событие практически невозможным, то практически достоверно попадание параметра  в доверительный интервал . Следовательно, можно положить с точностью .

2. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии. Пусть случайная величина  распределена по нормальному закону и известна дисперсия . Обозначим и, используя выборку x₁, x₂, ..., x_n, найдем интервальную оценку для параметра a, имеющую заданную надежность . Элементы выборки являются независимыми случайными величинами, распределенными так же, как и , поэтому их сумма, а значит, и среднее арифметическое распределено по нормальному закону, причем , (см. п. 6 § 1). Значит, функцией распределения для является , где .

Отсюда при любом  > 0 имеем , так что интервал является доверительным интервалом для параметра a с надежностью .

Подберем теперь  так, чтобы выполнялось равенство , или, что равносильно, . Так как функция  непрерывна и на промежутке возрастает от 0 до 1/2, то для любого числа , удовлетворяющего условию 0 <  < 1, существует единственное число такое, что . Положим , тогда , так что доверительный интервал для параметра a с заданной надежностью  имеет вид

.

Пример. Случайная величина распределена по нормальному закону и имеет дисперсию ²  4. Имеется выборка объема n  25, для которой получено . Найдем с надежностью   0,95 доверительный интервал для неизвестного параметра .

Имеем . Используя таблицу значений функции  (табл. 2), находим . Следовательно, , доверительный интервал: (11,516; 13,084), a  12,3  0,8.

3. Законы распределения ² и Стьюдента. Определение 1. Случайная величина называется распределенной по закону ² (хи‑квадрат), если она представляется в виде суммы , где случайные величины ₁, ₂, ..., _n попарно независимы и распределены по нормальному закону с параметрами M_k  0, D_k  1 (k  1, 2, …, n).

Число n называют числом степеней свободы распределения ².

Обычно пишут , т. е. для обозначения случайной величины, распределенной по закону ², используют одно и то же выражение, хотя она зависит как от числа слагаемых n, так и от самих слагаемых.

Можно доказать, что случайная величина ² непрерывна; ее плотность вероятностей  f (x) при x m 0 равна нулю (поскольку  ² не принимает отрицательных значений), а при x > 0 она имеет довольно сложное выражение: , где 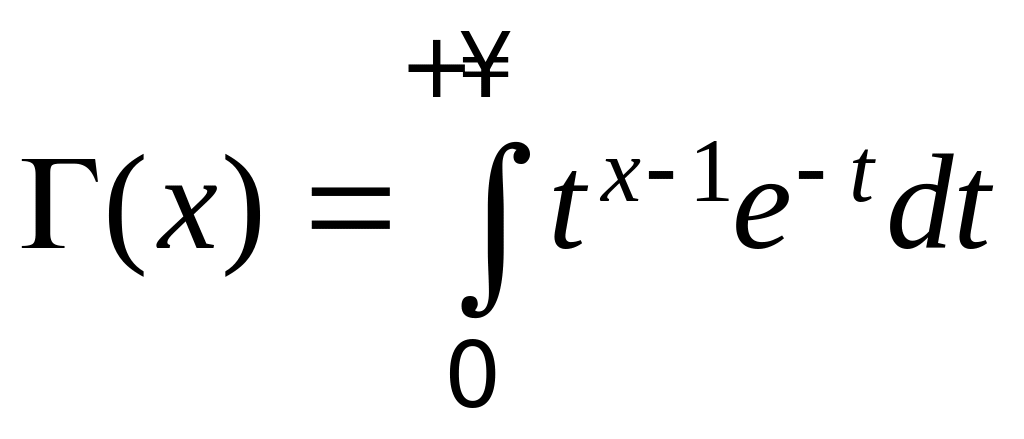– так называемая гамма-функция.

Рассмотрим важные случаи распределения ².

(а) Пусть – попарно независимые случайные величины, распределенные по нормальному закону, M_k  a_k, D_k  (k  1, 2, …, n). Тогда величины также попарно независимы и распределены по нормальному закону. При этом для каждого k  1, 2, …, n имеем M  0, D 1. Поэтому – случайная величина, распределенная по закону ² с n степенями свободы.

(б) Пусть и – независимые случайные величины, распределенные по закону ² соответственно с m и n степенями свободы. Тогда имеем и , где все ₁, ₂, ..., _mn – попарно независимые случайные величины, распределенные по нормальному закону, причем M_j  0, D_j 1 ( j  1, 2, …, m + n). Поскольку , получаем, что сумма распределена по закону с числом степеней свободы m + n.

(в) Пусть  – случайная величина, распределенная по нормальному закону, , – выборка значений  и s² – исправленная выборочная дисперсия, получающаяся для этой выборки по формуле (5) § 1. Рассмотрим при n > 1 случайную величину

.

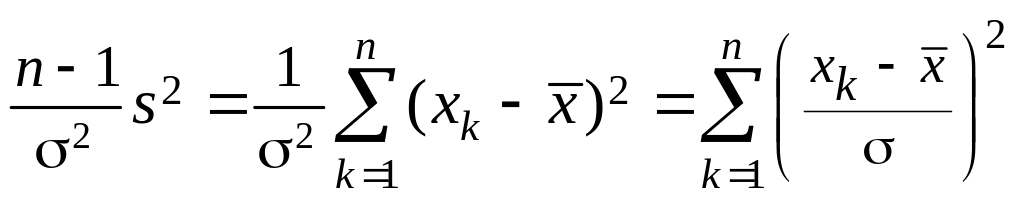Случайные величины в скобках распределены по нормальному закону (т. к. x_k и распределены по нормальному закону), при этом , однако < 1. К тому же эти случайные величины зависимы, т. к. 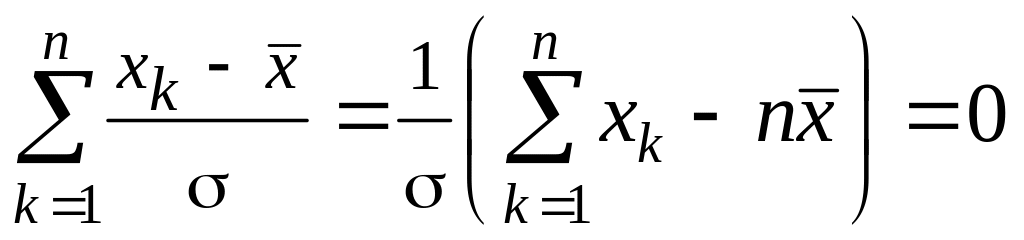. Однако можно доказать, что существуют независимые случайные величины ₁, ₂, ..., _n–1, линейно выражающиеся через x₁, x₂, ..., x_n (а значит, распределенные по нормальному закону) и такие, что , причем M_k  0, D_k  1 (k  1, 2, …, n – 1). Поэтому случайная величина распределена по закону ² с n – 1 степенями свободы.

Определение 2. Случайная величина называется распределенной по закону Стьюдента с n степенями свободы, если она представляется в виде , где  и  – независимые случайные величины, из которых первая распределена по нормальному закону с параметрами M  0 и D  1, а вторая – по закону с n степенями свободы.

Можно доказать, что случайная величина, распределенная по закону Стьюдента, непрерывна и имеет плотность вероятностей .

При эта функция стремится к , так что при неограниченном возрастании n распределение Стьюдента приближается к нормальному.

4. Доверительный интервал для дисперсии нормального распределения. Пусть случайная величина  распределена по нормальному закону. Построим интервальную оценку для неизвестной дисперсии M   c заданной надежностью , используя выборку значений , которые опять предполагаются независимыми случайными величинами, распределенными так же, как и .

Для этого рассмотрим случайную величину , распределенную по закону с n – 1 степенями свободы (см. п. 3 (в)). Пусть F – функция распределения этой случайной величины.

Поскольку функция F возрастает и непрерывна (т. к. является непрерывной случайной величиной), существуют и однозначно определены положительные числа y и z такие, что

, . (1)

Отсюда следует , т. е. . Неравенства , равносильны соответственно неравенствам и , так что получаем , значит, доверительный интервал для дисперсии с надежностью  имеет вид

.

Для нахождения y и z, удовлетворяющих условию (1), используют таблицу корней уравнения . Так как и , то для отыскания y нужно положить , а для отыскания z нужно положить .

Пример. Пусть для определения неизвестной дисперсии случайной величины, распределенной по нормальному закону, сделана выборка объемом n  18. Найдем доверительный интервал для ² с надежностью   0,96.

Имеем: , и в таблице 3 на пересечении строки, соответствующей числу степеней свободы 17, и столбца, соответствующего q  0,02, находим y = 7,3; , и по таблице находим z  31,0. Искомый доверительный интервал имеет вид .

5. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии. Пусть  – случайная величина, распределенная по нормальному закону, и параметры M  a и D  ² нам неизвестны. Пусть по результатам n испытаний найдены выборочное математическое ожидание и исправленная выборочная дисперсия s². Введем в рассмотрение случайные величины и . Первая распределена по нормальному закону, причем M₀  0, D₀  , а вторая – по закону с n – 1 степенями свободы (см. п. 3 (в)). Следовательно, случайная величина распределена по закону Стьюдента с n – 1 степенями свободы. По заданной надежности  можно найти такое число , чтобы выполнялось равенство:

. (2)

Неравенство в скобках равносильно двойному неравенству , которое, в свою очередь, равносильно следующему: . Поэтому (2) равносильно равенству , так что доверительный интервал для параметра a с надежностью  имеет вид

.

Для решения уравнения (2) составлена таблица корней уравнения . Число x ищется на пересечении строки с номером, соответствующим числу степеней свободы случайной величины t, и столбца, соответствующего значению .

Пример. Пусть получена выборка объема n  25 значений случайной величины , распределенной по нормальному закону, и пусть для этой выборки , . Найдем доверительный интервал для параметра M  a с надежностью   0,95.

Имеем . В таблице 4 на пересечении строки, соответствующей числу степеней свободы 24, и столбца, соответствующего   0,95, находим ;

.

Таким образом, требуемый интервал – .