Добавил:

420 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

Процессы и аппараты химической технологии

Файл:

Лекция 6 весеннего семестра

.pdf

Скачиваний:

Добавлен:

10.11.2019

Размер:

244.66 Кб

Скачать

☆

ЛЕКЦИЯ 6

ЕДИНИЦЫ ПЕРЕНОСА

Число единиц переноса – изменение рабочей концентрации, приходящееся на единицу движущей силы.

Для процесса абсорбции общее число единиц переноса, выраженное через относительные концентрации, может быть найдено через известную движущую силу:

N		=	Yн −Yк	, N		=	Xк − Xн	(6-1)
	Oy				Ox
			Yср				Xср

Аналогично общее число единиц переноса, выраженное через мольные доли, связано с движущей силой для верхней и нижней частей ректификационной колонны:

nниз =	yF − yW	, nверх =	yP − yF	(6-2)
	yF − yW
	yниз		yверх
Oy	yниз	Oy	yверх
	ср		ср

В общем случае число единиц переноса может быть найдено как интеграл от обратной разницы рабочей и равновесной концентраций:

– для абсорбции

Yн

Xк

NOy =

, NOx =

(6-3)

Y Y −Y *

X * −X

– для ректификации

nниз =

nверх =

(6-4)

y * −y

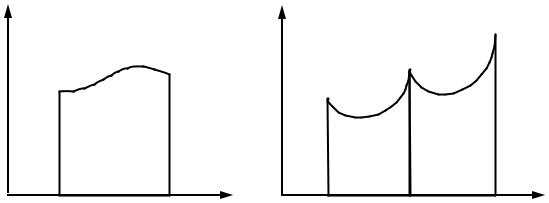
Нахождение интегралов графическим методом представлено на рис. 6-1.

Y–Y*

y*–y

	NOy
	NOy				nниз		nверх
					nниз		nверх
					Oy		Oy

Xн		Xк	X	xW		xF		xP x
	а					б

Рис. 6-1. Определение числа единиц переноса графическим интегрированием:

а – абсорбция, б – ректификация

Преобразование основного уравнения массопередачи

Рассмотрим преобразование метода расчёта высоты насадочных колонн через основное уравнение массопередачи в метод расчёта через единицы переноса на примере процесса абсорбции.

Основное уравнение массопередачи:

		JA = Ky A Yср = KyV V Yср							(6-5)
где Ky – поверхностный коэффициент массопередачи,						кмоль A		; KyV	– объёмный
где Ky – поверхностный коэффициент массопередачи,					2		кмоль A	; KyV	– объёмный
					м	с
					м	с	кмоль G
							кмоль G
		кмоль A
коэффициент массопередачи,				.
коэффициент массопередачи,	3		кмоль A	.
	м	с
	м	с	кмоль G
			кмоль G

Материальный баланс:

JA = nG (Yн −Yк ) = nL (Xк − Xн )

Высота насадки в колонном аппарате:
Hнас =	V	=	A
Hнас =	S	=	a S
	S		a S

Подставляя уравнения (6-5) и (6-6) в уравнение (6-7), получаем:

H		=	nG	Yн −Yк	=	nG	Yн −Yк	= h N
	нас								Oy
			KyV S Yср					Oy
						K y a S Yср
			hOy	NOy		hOy	NOy

Аналогичное выражение можно получить для жидкой фазы:

Xк − Xн

= h N

нас

KxV S Xср

Kx a S Xср

hOx

(6-6)

(6-7)

(6-8)

(6-9)

Аддитивность единиц переноса

Рассмотрим аддитивность единиц переноса на примере абсорбции, то есть вещество переходит из газовой фазы в жидкую. Полагаем процесс установившемся и протекающем в противоточном аппарате в режиме идеального вытеснения. Представим процесс в виде зависимости составов фаз от площади межфазной поверхности на рис. 6-1.

Для элемента межфазной поверхности dA количество вещества, переходящего из фазы в фазу (элементарный межфазный поток), может быть получен из материального баланса:

dJA = −nG dY = nL dX .

(6-10)

Знак «–» в уравнении (6-10) показывает, что газовая фаза обедняется ключевым компонентом.

X, Y

Yн
dY
		Y
		Y*
			Yк
		X*
Xк
dX		X	Xн
dX		X

0	dA		A	A
				A

Рис. 6-1. Зависимость составов фаз от площади межфазной поверхности
Элементарный межфазный поток также может быть получен через уравнения
массоотдачи:
dJA = y (Y −Yгр ) dA = x (Xгр − X ) dA ,					(6-11)
где Yгр и Xгр – соответственно составы газовой и жидкой фаз на границе раздела фаз.
Приравниваем выражение (6-11) к (6-10) для каждой из фаз:
−nG dY = y (Y −Yгр ) dA , nL dX = x (Xгр − X ) dA .					(6-12)

Разделяем переменные в уравнениях (6-12) и интегрируем по поверхности в пределах от 0

до A, по составу газовой фазы в пределах от Yн до Yк, а по составу жидкой фазы в пределах от Xн до Xк:

Yк

Xк

−

dA ,

dA .

(6-13)

Y −Y

− X

Yн

гр

Xн

гр

Для газовой фазы знак «–» можно убрать, поменяв местами пределы интегрирования.

После интегрирования уравнений (6-13) получаем выражения для частных чисел единиц переноса:

Yн

y A

Xк

, N

= x .

(6-14)

Y −Y

− X

гр

Yк

гр

Из уравнений (6-14) получаем выражения для коэффициентов массоотдачи:

			Ny nG				N		n
	y	=		,	x	=		x	L	(6-15)
		=	A	,		=		A		(6-15)


Элементарный межфазный поток может быть выражен и через уравнение
массопередачи:
dJA = −nG dY = Ky (Y −Y *) dA .										(6-16)

Разделяем переменные в уравнении (6-16) и интегрируем по поверхности в пределах от 0

до A, по составу газовой фазы в пределах от Yн до Yк:

Yк	dY		Ky	A
−		=		dA .	(6-17)
	Y −Y *		n
Yн			G	0

После интегрирования уравнения (6-17) получаем выражение для общего числа единиц переноса по газовой фазе:

Yн

Ky A

NOy =

(6-18)

Y −Y *

Из уравнения (6-18) получаем выражение для коэффициента массопередачи:

NOy nG

(6-19)

Запишем уравнение аддитивности диффузионных сопротивлений:

(6-20)

Подставим в уравнение (6-20) выражения (6-19) и (6-15) получаем:

A m

(6-21)

NOy nG

Ny nG

Nx nL

Преобразуя уравнение (6-21) получаем формулу аддитивности единиц переноса:

+ m

(6-22)

NOy

1 F

где Fм =

– фактор массопередачи.

Аналогично для жидкой фазы получаем:

+ F

(6-23)

NOx

Сопоставив выражения (6-22) и (6-23), получаем:

NOy = Fм NOx .

(6-24)

По аналогии с выводом уравнения (6-23), используя уравнения (6-8) и (6-9), можно получить уравнение для определения высоты общей единицы переноса через высоты частных единиц переноса:

h	= h +		hx	, h	= h + F h ,	(6-25)

Oy	y		Fм	Ox	x м y

откуда получаем связь высот общих единиц переноса:
		hOx = Fм hOy .				(6-26)

Влияние продольного перемешивания на движущую силу

Под продольным перемешиванием понимают циркуляцию фаз в направлении противоположном движению потоков, а также поперечную неравномерность потоков.

Влияние продольного перемешивания сказывается на уменьшение средней движущей силы процесса массопередачи и, следовательно, скорости массопередачи. Обратное перемешивание сильно возрастает с увеличением отношения диаметра аппарата к его длине.

Расчет влияния обратного перемешивания на среднюю движущую силу массопередачи или число единиц переноса возможен с той или иной степенью точности при помощи различных упрощенных моделей перемешивания, например диффузионной модели или ячеечной модели.

Объёмные коэффициенты массопередачи

Высота единиц переноса является кинетической характеристикой для аппаратов с непрерывным контактом фаз. Более общей характеристикой как для аппаратов с непрерывным контактом фаз, так и для аппаратов со ступенчатым контактом фаз является

объём единицы переноса, т.е. рабочий объём массообменного аппарата, соответствующий по эффективности разделения одной единице переноса:

V = vOy NOy .			(6-27)
Выражаем из уравнения (6-5) объём аппарата:
	J A
V =		.	(6-28)
	KyV Yср

Подставляем в уравнение (6-28) выражение (6-6) для межфазного потока:

V =	nG (Yн −Yк )	=	nG	N		.	(6-29)
					Oy
	KyV Yср		KyV

Сопоставляя выражения (6-27) и (6-29), получаем:

v =

(6-30)

Oy KyV

Аналогично для жидкой фазы:

v =

(6-31)

Ox KxV

Объёмные коэффициенты массопередачи находятся по уравнению аддитивности,

аналогичному (6-20), через объёмные коэффициенты массоотдачи:

1	=	1	+	m	,	(6-32)
KyV
		yV		xV

либо пересчитывая поверхностные коэффициенты массопередачи в объёмные с помощью удельной поверхности:

KyV = a Ky .

(6-33)

Соседние файлы в папке лекции

#
10.11.2019643.78 Кб24Лекция 16 весеннего семестра.pdf
#
10.11.2019430.09 Кб26Лекция 2 весеннего семестра.pdf
#
10.11.2019387.8 Кб22Лекция 3 весеннего семестра.pdf
#
10.11.2019290.48 Кб22Лекция 4 весеннего семестра.pdf
#
10.11.2019295.99 Кб21Лекция 5 весеннего семестра.pdf
#
10.11.2019244.66 Кб22Лекция 6 весеннего семестра.pdf
#
10.11.2019249.35 Кб24Лекция 7 весеннего семестра.pdf
#
10.11.2019375.83 Кб22Лекция 8 весеннего семестра.pdf
#
10.11.2019229.63 Кб21Лекция 9 весеннего семестра.pdf