- •Міністерство освіти і науки україни
- •Методичні вказівки
- •Практичне заняття №1 спектри періодичних сигналів
- •1.1 Мета заняття
- •1.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •1.3 Задачі для самостійної роботи
- •1.4 Контрольні запитання і завдання
- •Практичне заняття №2 спектри неперіодичних сигналів
- •2.1 Мета заняття
- •2.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •2.3 Задачі для самостійної роботи
- •2.4 Контрольні запитання і завдання
- •3.1 Мета заняття
- •3.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,8].
- •3.3 Задачі для самостійної роботи
- •3.4 Контрольні запитання і завдання
- •Практичне заняття №4 ентропія та її властивості
- •4.1 Мета заняття
- •4.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,7,9].
- •4.3 Задачі для самостійної роботи
- •4.4 Контрольні запитання і завдання
- •Практичне заняття №5 ентропія неперервних джерел інформації
- •5.1 Мета заняття
- •5.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •5.3 Задачі для самостійної роботи
- •5.4 Контрольні запитання і завдання
- •Практичне заняття №6 ефективне кодування
- •6.1 Мета заняття
- •6.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •6.3 Задачі для самостійної роботи
- •6.4 Контрольні запитання і завдання
- •Практичне заняття №7
- •7.1 Мета заняття
- •7.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •7.3 Задачі для самостійної роботи
- •7.4 Контрольні запитання і завдання
- •Практичне заняття №8 циклічні коди
- •8.1 Мета заняття
- •8.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •8.3 Задачі для самостійної роботи
- •8.4 Контрольні запитання і завдання
- •Навчальне видання методичні вказівки
- •Хнуре. Україна. 61166, Харків, просп. Леніна, 14 Віддруковано в навчально-науковому
- •61166, Харків, просп. Леніна, 14
4.3 Задачі для самостійної роботи
4.3.1 Два дискретні джерела інформації задані матрицями
 и.
и.
Визначити,
яке джерело має більшу невизначеність
у випадку, якщо: а)
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() .
.
4.3.2 На
виході двійкового джерела інформації
елементи «0» і «1» з'являються з
ймовірностями відповідно
й
![]() .
При якому значенні
ентропія джерела є максимальною?
Побудувати графік
.
При якому значенні
ентропія джерела є максимальною?
Побудувати графік
![]() для двійкового джерела.
для двійкового джерела.
4.3.3 Довести властивість екстремальності ентропії. Для дискретного джерела
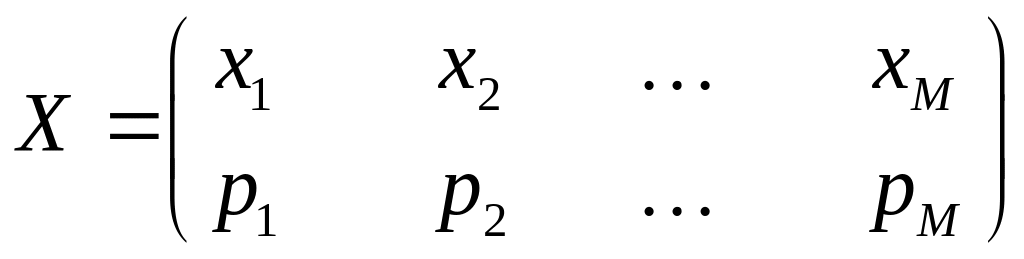
ентропія
 є
максимальною і дорівнює
є
максимальною і дорівнює
![]() у випадку, якщо елементи рівноймовірні:
у випадку, якщо елементи рівноймовірні:
![]() .
.
4.3.4 Дискретне
джерело інформації задано матрицею
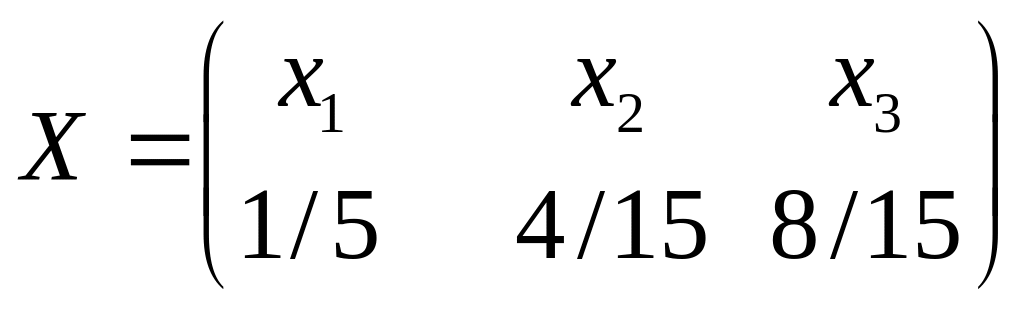 .
Обчислити його середню невизначеність
і порівняти отримане значення з ентропією
наступного джерела
.
Обчислити його середню невизначеність
і порівняти отримане значення з ентропією
наступного джерела
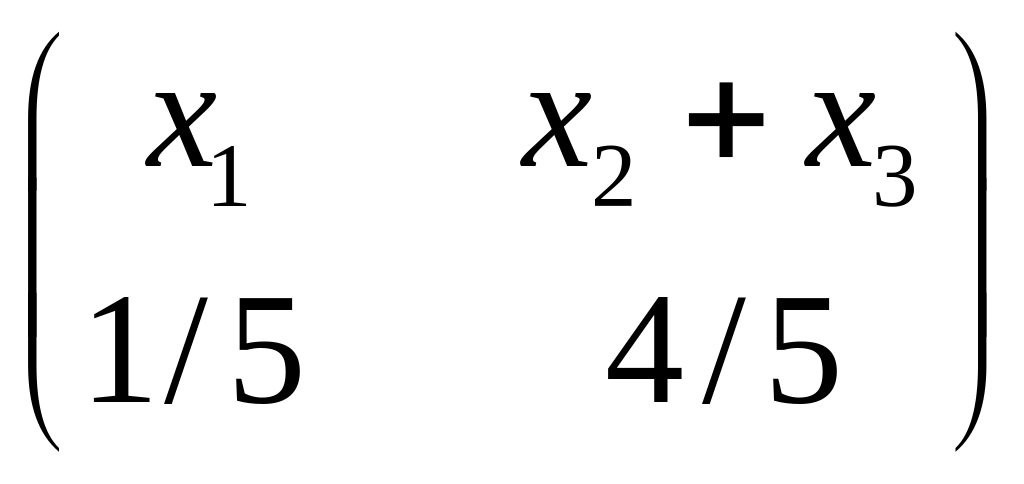 .
.
4.3.5 Обчислити
ентропії трьох систем
 ;
;
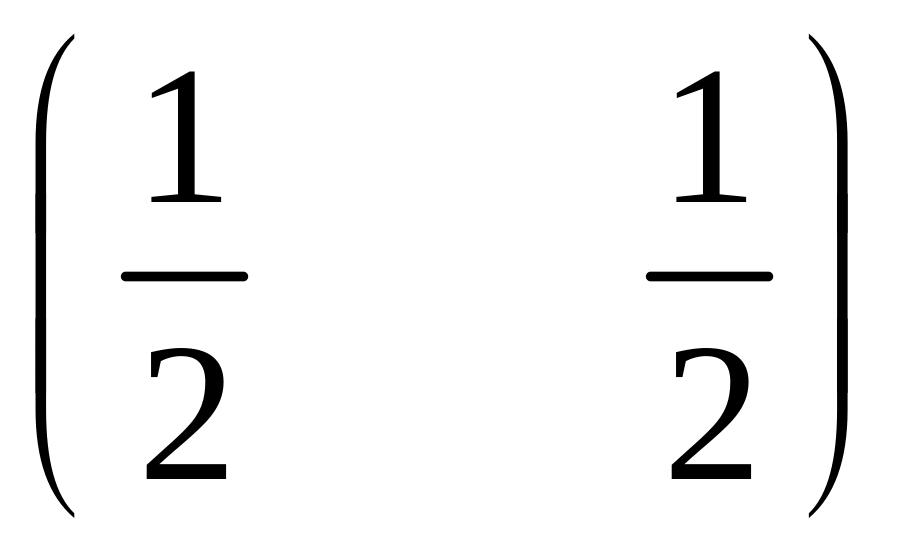 і
і
 .
Пояснити на цьому прикладі властивість
безперервності ентропії.
.
Пояснити на цьому прикладі властивість
безперервності ентропії.
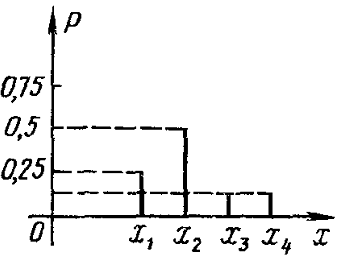
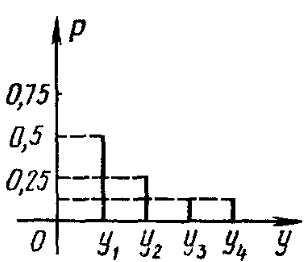
4.3.6 Визначити невизначеності двох систем і (рис.4.1).
|
|
Рис.4.1 Імовірності станів двох дискретних систем |
|
4.3.7 Перевірити
властивість адитивності
ентропії на прикладі джерела
 .
.
4.3.8 Нехай
і
- два алфавіти;
![]() .
Чому дорівнює умовна ентропія
.
Чому дорівнює умовна ентропія
![]() ,
якщо: а)
і
незалежні; б)
і
залежні; в)
,
якщо: а)
і
незалежні; б)
і
залежні; в)
![]() .
.
4.3.9 Елементи
алфавітів
і
статистично пов'язані. Відомо, що
![]() біт,
біт,
![]() біт.
У яких межах змінюється умовна ентропія
біт.
У яких межах змінюється умовна ентропія
![]() при зміні
в максимально можливих межах?
при зміні
в максимально можливих межах?
4.3.10 Ракети двох пускових установок використовуються для поразки двох цілей. Ракета першої установки вражає ціль номер 1 з імовірністю 0,5; ціль номер 2 - з імовірністю 0,3 і дає промах з імовірністю 0,2. Ракета другої установки вражає першу ціль з імовірністю 0,3, другу - з імовірністю 0,5 і ймовірність промаху дорівнює 0,2. Імовірність вибору першої установки дорівнює 0,4. Чому дорівнює невизначеність вибору установки, якщо відомо, що уражено другу ціль; якщо відбувся промах; яка невизначеність результату, якщо пущено будь-яку ракету?
4.3.11 За
заданим значенням
і
знайти
,
якщо
![]() біт.
біт.
4.3.12 Матриця спільних ймовірностей двох джерел дорівнює:
 .
.
Визначити ентропії
,
![]() ,
,
,
,
,
,
![]() ,
,
![]() ,
,
![]() .
.
4.3.13 Визначити максимальну ентропію телевізійного зображення, яке містить 500 рядків по 650 елементів у рядку, за умови, що яскравість кожного елемента передається за допомогою 8 квантованих некорельованих рівнів.
4.3.14 У якому співвідношенні знаходяться відомі одиниці кількості інформації: двійкова (біт), натуральна (ніт), десяткова (діт)?
4.3.15 Маємо
значення
й
.
У яких межах може змінюватися
![]() при зміні
від мінімального до максимального
можливого значень?
при зміні
від мінімального до максимального
можливого значень?
4.3.16 Визначити
середню
кількість інформації
,
якщо матриця системи передачі інформації
![]() має вигляд
має вигляд
 .
.
4.3.17 Визначити середню кількість інформації у системі, яку задано матрицею
.
4.3.18 Обчислити
середню кількість інформації
![]() про передані повідомлення
про передані повідомлення
![]() ,
що доставляється прийнятим повідомленням
,
що доставляється прийнятим повідомленням
![]() ансамблю
ансамблю
![]() ,
якщо система передачі описується
матрицею
,
якщо система передачі описується
матрицею
 .
.
4.3.19 Радіостанція
може працювати на хвилі
![]() (подія
(подія
![]() )
або на хвилі
)
або на хвилі
![]() (подія
(подія
![]() );
в імпульсному (подія
);
в імпульсному (подія
![]() )
або в неперервному (подія
)
або в неперервному (подія
![]() )
режимах. Імовірності спільних подій
мають наступні значення:
)
режимах. Імовірності спільних подій
мають наступні значення:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Обчислити кількість інформації, яку
отримано щодо режиму роботи станції,
якщо стане відомою довжина хвилі.
.
Обчислити кількість інформації, яку
отримано щодо режиму роботи станції,
якщо стане відомою довжина хвилі.
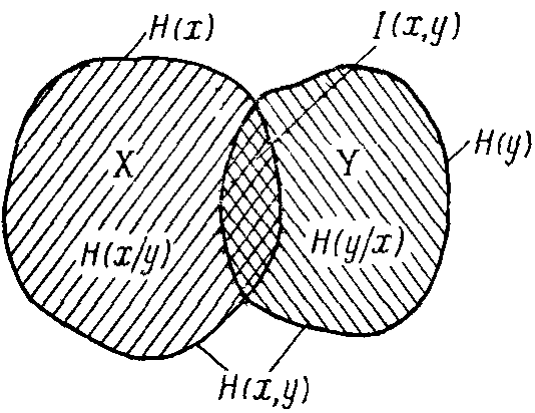
4.3.20 На рис.4.2, а показано приклади
діаграм Вінера, що характеризують
співвідношення між ентропійними
оцінками. Виділені ділянки плоских
фігур відповідають різним умовним та
безумовним середнім ентропіям. Об'єднання
фігур виражає об'єднану ентропію
,
перетинання – взаємну інформацію
та т.і. За аналогією із двовимірним
випадком позначити елементи тривимірної
системи (рис.4.2, б), тобто ентропії
![]() ,
,
![]() ,
,
![]() ,
,
![]() та т.і.
та т.і.
|
|
а) |
б) |
Рис.4.2 Діаграми Вінера |
|
4.3.21 Є
три дискретних джерела інформації
 ,
,
 і
і
 ,
,
![]() .
.
Визначити, яке джерело має найбільшу невизначеність.
4.3.22 Число
символів алфавіту джерела
![]() (
(![]() або
або
![]() ).
Імовірності появи символів джерела
).
Імовірності появи символів джерела
![]() ;
;
![]() ;
;
![]() та
та
![]() .
Між сусідніми символами є кореляційні
зв'язки,
які описуються матрицею умовних
ймовірностей
.
Між сусідніми символами є кореляційні
зв'язки,
які описуються матрицею умовних
ймовірностей
![]() наступного виду
наступного виду
 ,
наприклад,
,
наприклад,
![]() .
.
Визначити ентропію джерела.
4.3.23 Ансамблі подій і об'єднані, причому ймовірності спільних подій визначаються матрицею спільних ймовірностей
 ,
наприклад,
,
наприклад,
![]() .
.
Визначити ентропії ансамблів і ; ентропію об'єднаного ансамблю; умовні ентропії ансамблів.
4.3.24 До
лінії зв'язку надходять рівноймовірні
й статистично незалежні дискретні
сигнали
![]() й
й
![]() .
Через дію
перешкод на виході каналу зв'язку
формуються сигнали
.
Через дію
перешкод на виході каналу зв'язку
формуються сигнали
![]() ,
,
![]() і
і
![]() з
матрицею умовних ймовірностей
з
матрицею умовних ймовірностей
 .
.
Визначити
повну взаємну інформацію
![]() .
.
4.3.25 По
каналу
зв'язку
з
однаковими ймовірностями передаються
![]() статистично незалежних
сигналів
статистично незалежних
сигналів
![]() (
(![]() ). При відсутності
перешкод переданому сигналу
). При відсутності
перешкод переданому сигналу
![]() відповідає на виході каналу сигнал
відповідає на виході каналу сигнал
![]() (
(![]() ). При наявності
перешкод кожний
переданий сигнал може бути лише з
імовірністю
). При наявності
перешкод кожний
переданий сигнал може бути лише з
імовірністю
![]() прийнятий правильно, а й з
імовірністю
як один з інших вихідних сигналів.
прийнятий правильно, а й з
імовірністю
як один з інших вихідних сигналів.
Визначити середню кількість інформації на один сигнал, яку передано по каналу за наявності та відсутності перешкод.
4.3.26 Система
передачі інформації характеризується
при
![]() ,
,
![]() матрицею спільних ймовірностей
матрицею спільних ймовірностей
 .
.
Визначити середню кількість взаємної інформації .
4.3.27 Радіолокаційна
станція РЛС
може працювати в метровому діапазоні
![]() або в дециметровому діапазоні
або в дециметровому діапазоні
![]() ,
а також у режимі огляду
,
а також у режимі огляду
![]() або в режимі наведення
або в режимі наведення
![]() .
Спільні ймовірності
цих подій описуються матрицею
.
Спільні ймовірності
цих подій описуються матрицею
 .
.
Обчислити кількість
часткової
інформації
![]() ,
яку одержано
щодо режиму
,
яку одержано
щодо режиму
![]() роботи РЛС,
якщо система виявлення повідомляє
діапазон
роботи РЛС,
якщо система виявлення повідомляє
діапазон
![]() роботи станції.
роботи станції.
4.3.28 Система передачі інформації характеризується матрицею спільних ймовірностей
.
Визначити середню кількість
взаємної інформації
та кількість часткової інформації
![]() ,
яка міститься в повідомленні
приймача про джерело
в цілому.
,
яка міститься в повідомленні
приймача про джерело
в цілому.
4.3.29 Ентропії
трьох дискретних випадкових величин
![]() є рівними:
є рівними:
![]() .
Визначити, чому дорівнює
,
якщо: а)
.
Визначити, чому дорівнює
,
якщо: а)
![]() ,
б)
,
б)
![]() .
Довести, що в загальному випадку
.
Довести, що в загальному випадку
![]() .
.