
- •Міністерство освіти і науки україни
- •Методичні вказівки
- •Практичне заняття №1 спектри періодичних сигналів
- •1.1 Мета заняття
- •1.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •1.3 Задачі для самостійної роботи
- •1.4 Контрольні запитання і завдання
- •Практичне заняття №2 спектри неперіодичних сигналів
- •2.1 Мета заняття
- •2.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •2.3 Задачі для самостійної роботи
- •2.4 Контрольні запитання і завдання
- •3.1 Мета заняття
- •3.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,8].
- •3.3 Задачі для самостійної роботи
- •3.4 Контрольні запитання і завдання
- •Практичне заняття №4 ентропія та її властивості
- •4.1 Мета заняття
- •4.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,7,9].
- •4.3 Задачі для самостійної роботи
- •4.4 Контрольні запитання і завдання
- •Практичне заняття №5 ентропія неперервних джерел інформації
- •5.1 Мета заняття
- •5.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •5.3 Задачі для самостійної роботи
- •5.4 Контрольні запитання і завдання
- •Практичне заняття №6 ефективне кодування
- •6.1 Мета заняття
- •6.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •6.3 Задачі для самостійної роботи
- •6.4 Контрольні запитання і завдання
- •Практичне заняття №7
- •7.1 Мета заняття
- •7.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •7.3 Задачі для самостійної роботи
- •7.4 Контрольні запитання і завдання
- •Практичне заняття №8 циклічні коди
- •8.1 Мета заняття
- •8.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •8.3 Задачі для самостійної роботи
- •8.4 Контрольні запитання і завдання
- •Навчальне видання методичні вказівки
- •Хнуре. Україна. 61166, Харків, просп. Леніна, 14 Віддруковано в навчально-науковому
- •61166, Харків, просп. Леніна, 14
Практичне заняття №1 спектри періодичних сигналів
1.1 Мета заняття
Метою заняття є вивчення студентами методів спектрального аналізу періодичних сигналів.
1.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
Спектральний метод передбачає опис сигналу у вигляді суми (інтегралу) гармонійних коливань (гармонік).
Сукупність усіх гармонійних складових сигналу називається спектром сигналу.
Сигнал
![]() ,
який представлено у вигляді суми
гармонік, може бути записаний наступним
чином:
,
який представлено у вигляді суми
гармонік, може бути записаний наступним
чином:
|
(1.1) |
У цій аналітичній формі запису сигнал представлено сумою речовинних гармонічних складових. Спектр сигналу (1.1) дискретний.
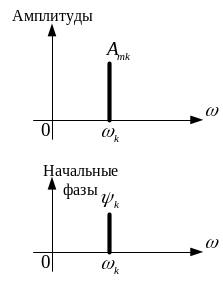
Рис.1.1,а відображує амплітудно-частотний спектр (АЧС) сигналу (1.1), тобто залежність амплітуд комплексного дискретного спектра від частоти. Рис.1.1,б відображує фазочастотний спектр (ФЧС) сигналу (1.1), тобто залежність початкових фаз складових комплексного дискретного спектра від частоти.
|
а) |
|
б) |
Рисунок 1.1 - АЧС і ФЧС сигналу |
Кожну з речовинних гармонік спектра можна представити в різних комплексних формах запису.
Речовинна гармоніка може, зокрема, розглядатися як речовинна частина комплексної величини:
|
(1.2) |
Комплексна величина
![]() відповідає вектору довжиною
відповідає вектору довжиною
![]() з початковою фазою
з початковою фазою
![]() ,
який обертається з кутовою швидкістю
,
який обертається з кутовою швидкістю
![]()
Речовинна гармоніка визначається в будь-який момент часу як проекція цього вектору на вісь абсцис (рис.1.2).
Речовинну гармоніку можна записати у вигляді суми двох комплексних гармонік:
|
(1.3) |
де ![]() - величина, комплексно-сполучена до
- величина, комплексно-сполучена до
![]() .
.
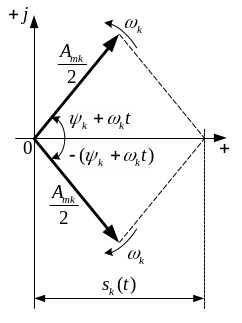
На комплексній площині такий
запис відповідає двом векторам довжиною
![]() з початковою фазою
з початковою фазою
![]() .
Вектори обертаються в різні сторони з
кутовою швидкістю
.
Речовинна гармоніка визначається в
будь-який момент часу як сума двох
векторів (рис.1.3).
.
Вектори обертаються в різні сторони з
кутовою швидкістю
.
Речовинна гармоніка визначається в
будь-який момент часу як сума двох
векторів (рис.1.3).
|
|
Рисунок 1.2 - Речовинна гармоніка |
Рисунок 1.3 - Речовинна гармоніка як сума двох комплексно-сполучених векторів |
Графічне зображення спектру
може відповідати різним формам його
запису. На рис.1.4 показано одну з гармонік,
причому рис.1.4,а
відповідає речовинній формі запису, а
рис.1.4,б
– комплексній формі. У речовинній формі
кожна складова спектра зображується у
вигляді однієї лінії на частоті
.
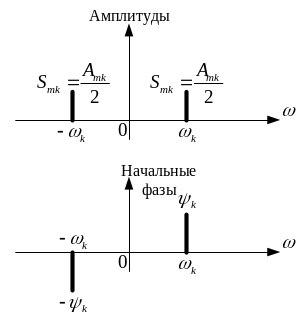
У комплексній формі кожна складова
відповідає парі ліній на частотах
![]() .
Графік АЧС є парною
функцією частоти, а графік ФЧС - непарною.
.
Графік АЧС є парною
функцією частоти, а графік ФЧС - непарною.
Для переходу від зображення речовинних гармонік до комплексних гармонік всі амплітуди зменшуються у два рази та відображуються для відповідних позитивних і негативних частот. Постійна складова спектра при переході від однієї форми до іншої не змінюється. Початкові фази в області негативних частот змінюють знак.
|
|
а) |
б) |
Рисунок 1.4 - Форми графічного зображення складових комплексного спектру |
|
Для спектрального аналізу сигналів використовуються:
тригонометричні перетворення;
ряд Фур'є;
інтеграл Фур'є.
Для спектрального аналізу періодичних сигналів використовується ряд Фур'є.
Періодичним сигналом будемо називати сигнал, для якого є чинним рівняння:
|
(1.4) |
де: n - цілі числа від - ∞ до + ∞;
T - період повторення функції.
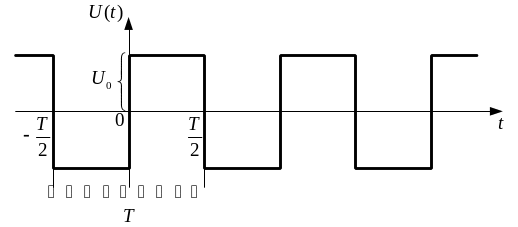
Найпростіший приклад періодичної функції - меандр:
|
Рисунок 1.5 - Періодичний сигнал „меандр” |
При спектральному аналізі періодичних сигналів мається на увазі, що сигнал існує в часі від -∞ до +∞.
Ряд Фур'є можна записати у наступній формі:
|
(1.5) |
де ![]() - частота першої гармоніки;
- частота першої гармоніки;
![]() - комплексні амплітуди
(комплексний спектр) комплексної форми
запису ряду Фур'є:
- комплексні амплітуди
(комплексний спектр) комплексної форми
запису ряду Фур'є:
 ;
;
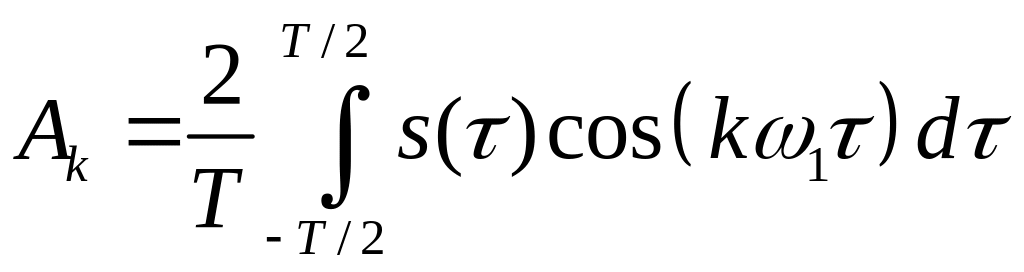 ;
;
![]() ;
;
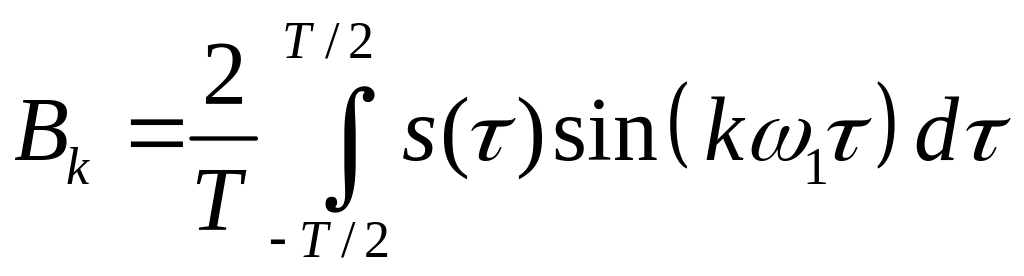 .
.
Таким чином, періодичну функцію можна представити у вигляді суми:
- постійного члена
![]() (середнього значення функції
);
(середнього значення функції
);
- деякої множини синусоїдальних
членів з частотами
![]() (основної частоти),
(основної частоти),
![]() ( 2-ї гармоніки),
( 2-ї гармоніки),
![]() ( 3-ї гармоніки), …
( 3-ї гармоніки), …
![]() -та
гармоніка
-та
гармоніка
![]() має частоту
має частоту
![]() ,
кругову частоту
,
кругову частоту
![]() ,
амплітуду
,
амплітуду
![]() та фазу
та фазу
![]() .
.
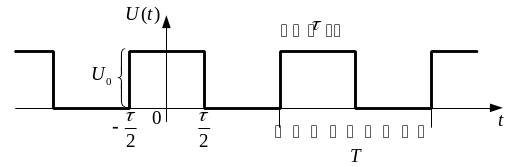
Приклад 1.1. Розрахувати спектри амплітуд і фаз періодичної послідовності прямокутних імпульсів тривалістю τ, що мають амплітуду U0 та період T (рис. 1.6).
|
|
Рисунок 1.6 - Періодична послідовність прямокутних імпульсів |
|
|
|
де ![]() .
.
Відомо, що
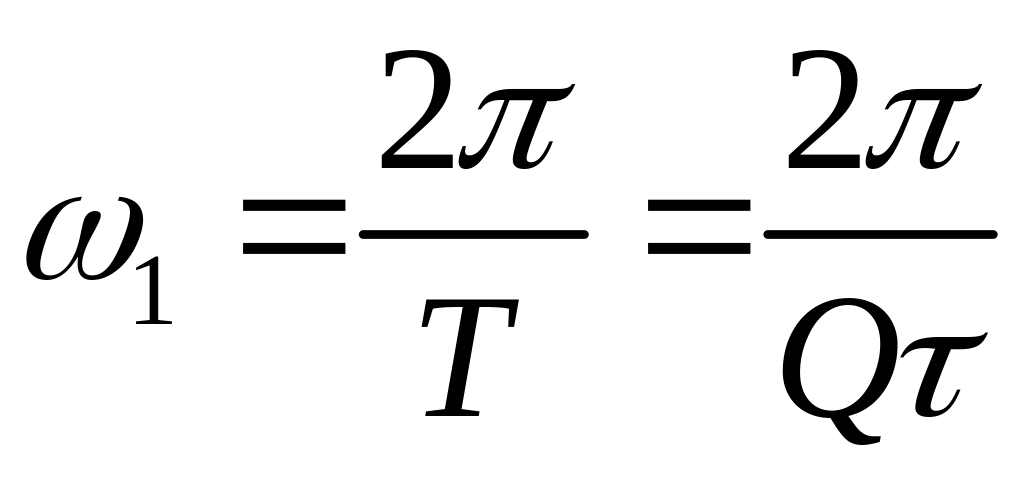 ,
тоді амплітудно-частотний спектр
дорівнює
,
тоді амплітудно-частотний спектр
дорівнює
|
|
або
|
|
де
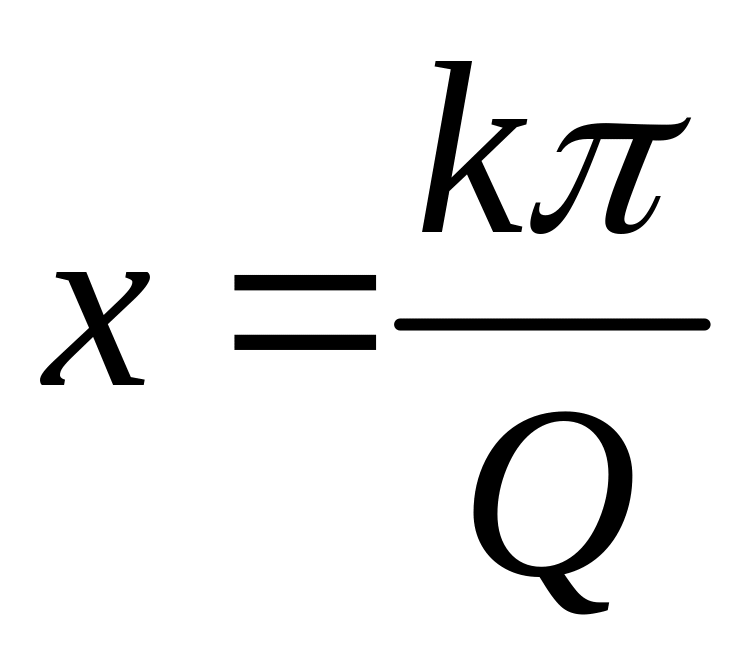 .
.
Позитивним значенням
![]() відповідають нульові початкові фази,
негативним – початкові фази, рівні
відповідають нульові початкові фази,
негативним – початкові фази, рівні
![]() ,
тому що
,
тому що
![]() .
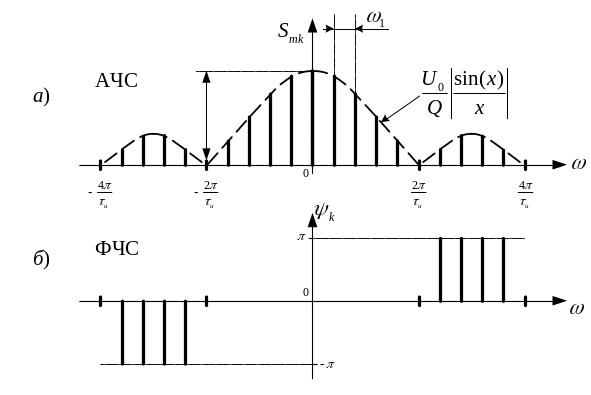
Графіки амплітудно- і фазочастотного
спектрів наведено на рис.1.7.
.
Графіки амплітудно- і фазочастотного
спектрів наведено на рис.1.7.
Огинаюча АЧС (показана на
рис.1.7 пунктирною лінією) змінюється за
законом
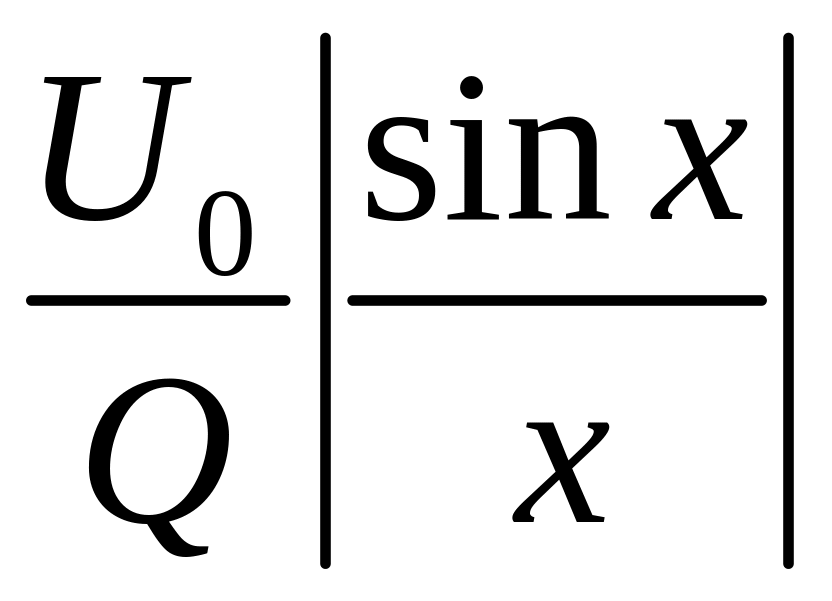 .
Гармоніки мають частоти
.
Гармоніки мають частоти
![]() (постійна складова)
(постійна складова)
![]() .
Коли номер гармоніки
стає кратним шпаруватості
.
Коли номер гармоніки
стає кратним шпаруватості
![]() ,
,
![]() і амплітуди відповідних гармонік
обертаються в нуль. Це відбувається на
частотах
і амплітуди відповідних гармонік
обертаються в нуль. Це відбувається на
частотах
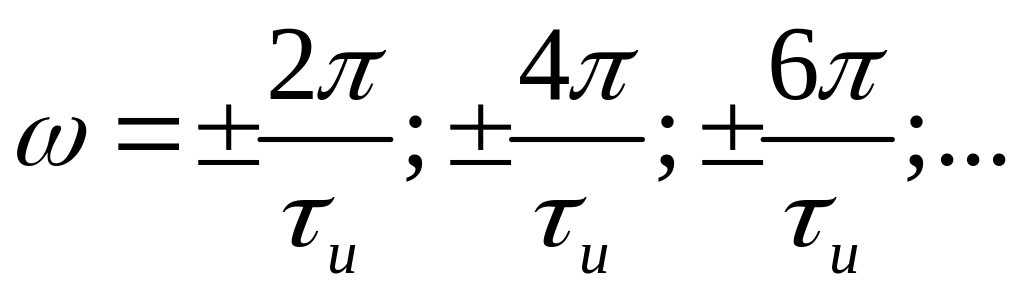 .
Рис. 1.7 відповідає випадку, коли
.
Рис. 1.7 відповідає випадку, коли
![]() ,
тому гармонічні складові з номерами
,
тому гармонічні складові з номерами
![]() мають нульові амплітуди.
мають нульові амплітуди.
|
Рисунок 1.7 - Спектри амплітуд і фаз періодичної послідовності прямокутних імпульсів |
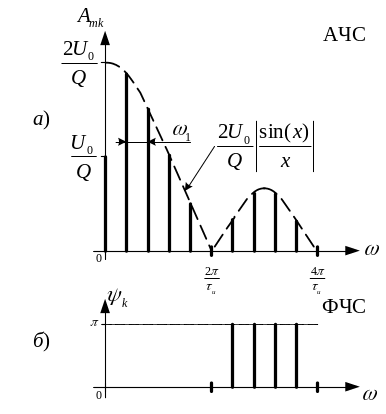
Від амплітудно- і фазочастотних спектрів комплексних гармонік ряду Фур'є можна перейти до речовинної форми запису ряду Фур'є. Для цього досить подвоїти всі амплітуди гармонік (крім постійної складової). Спектр буде містити складові лише з позитивними (тобто реально існуючими) частотами. Речовинні амплітудно- і фазочастотний спектри представлено на рис.1.8.
|
Рисунок 1.8 - Речовинні амплітудно- і фазочастотний спектри |
Переходячи від комплексної форми запису ряду до речовинної, отримуємо наступну аналітичну форму запису для спектра періодичної послідовності прямокутних імпульсів:
|
|
де
![]() при
при
![]() й
й
![]() при
при
![]() .
.
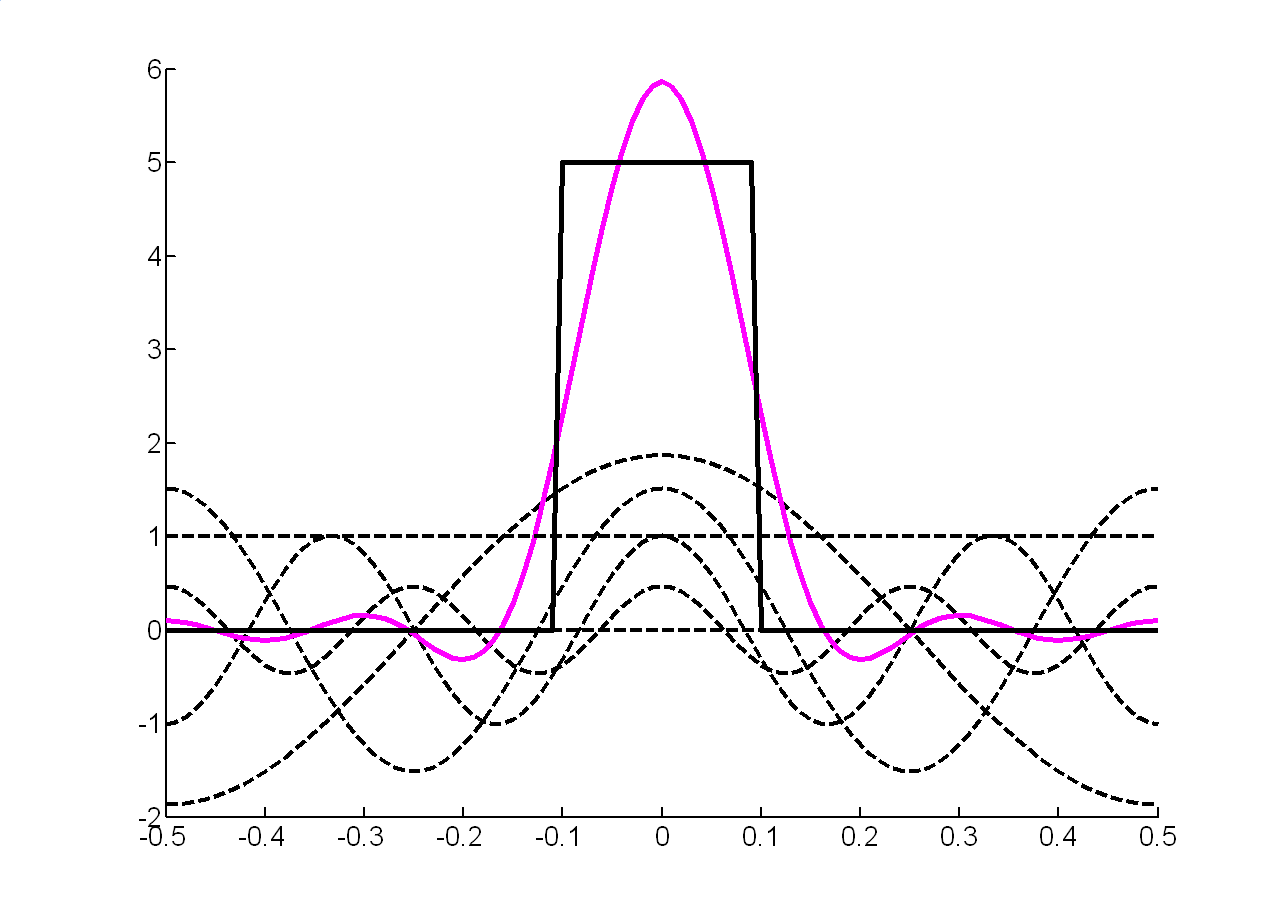
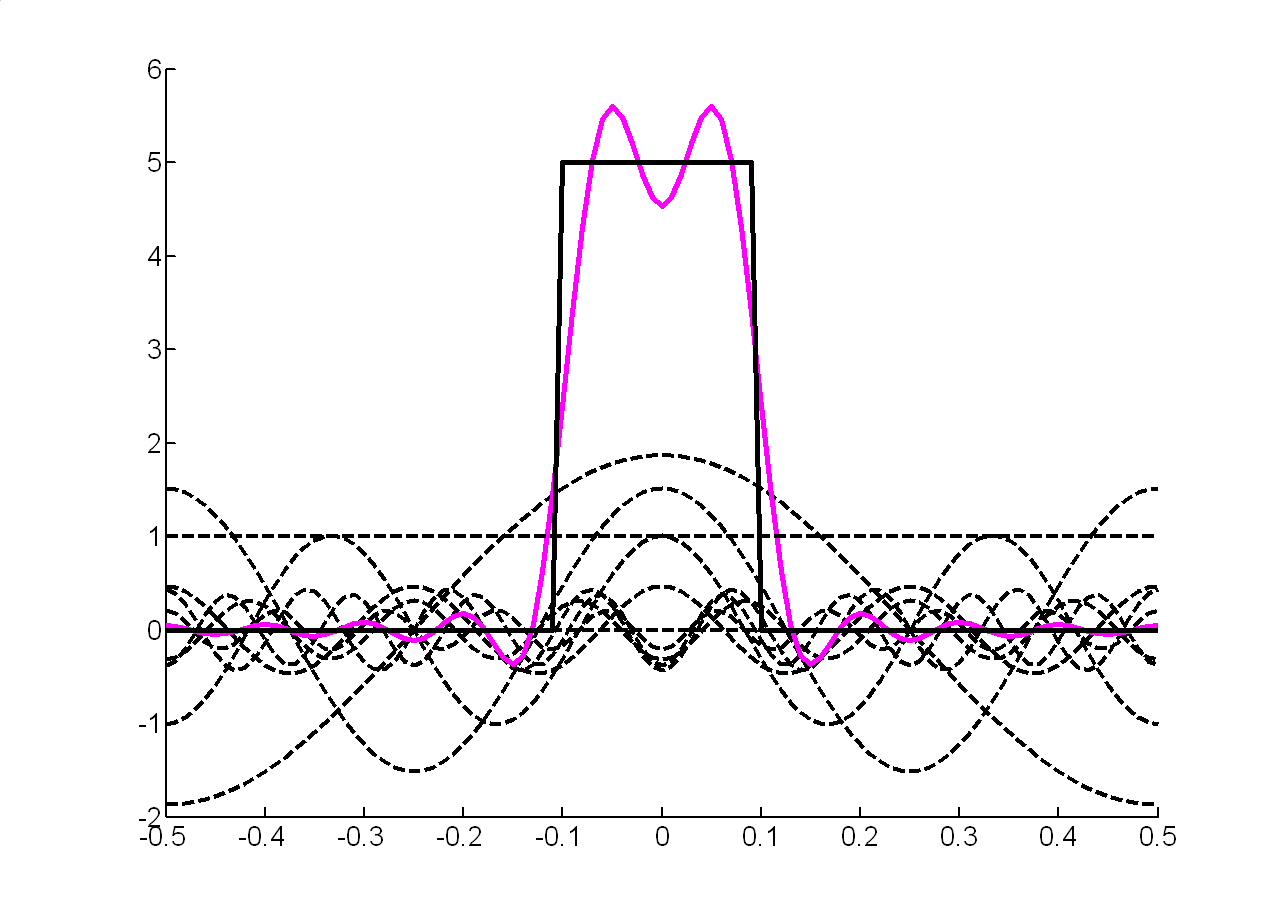
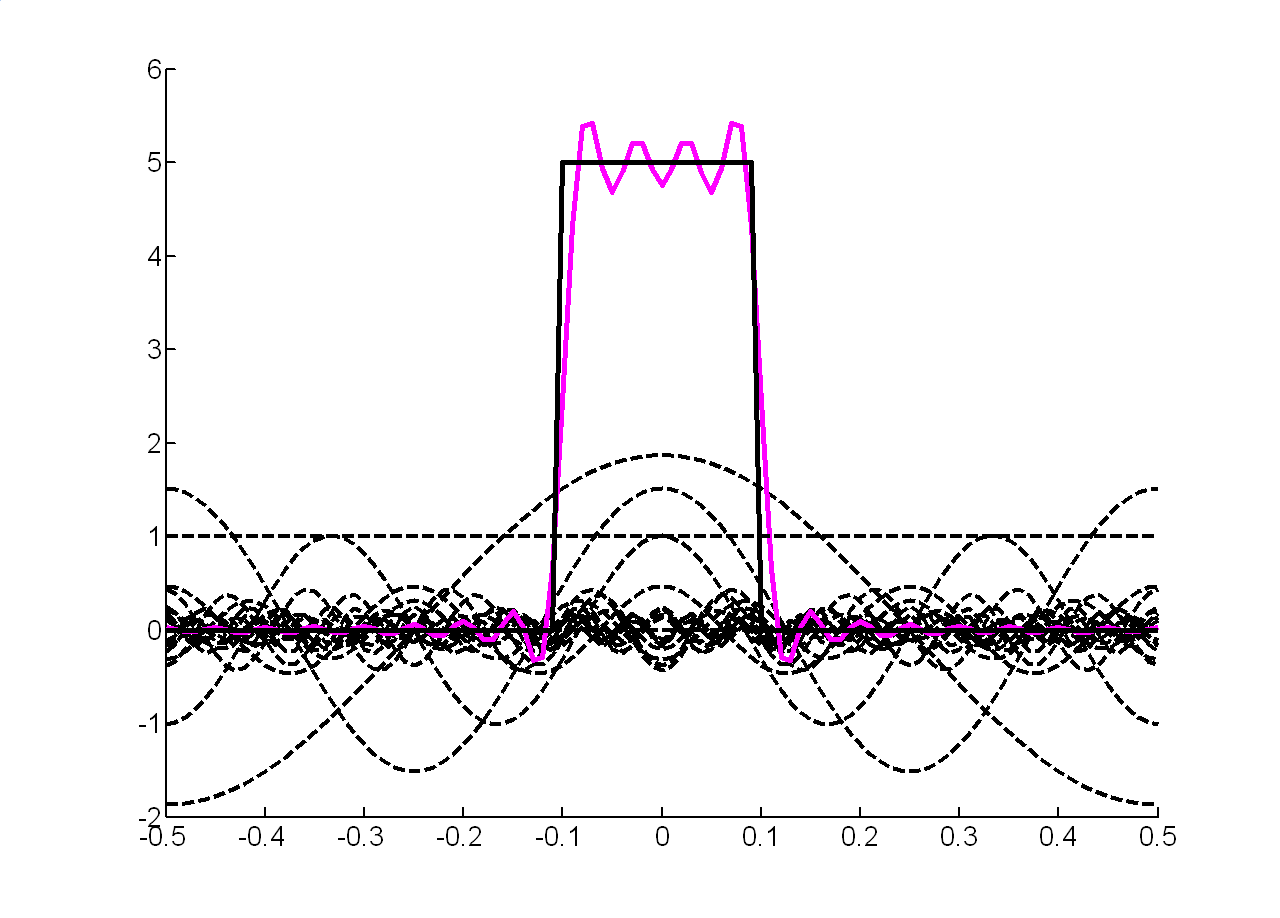
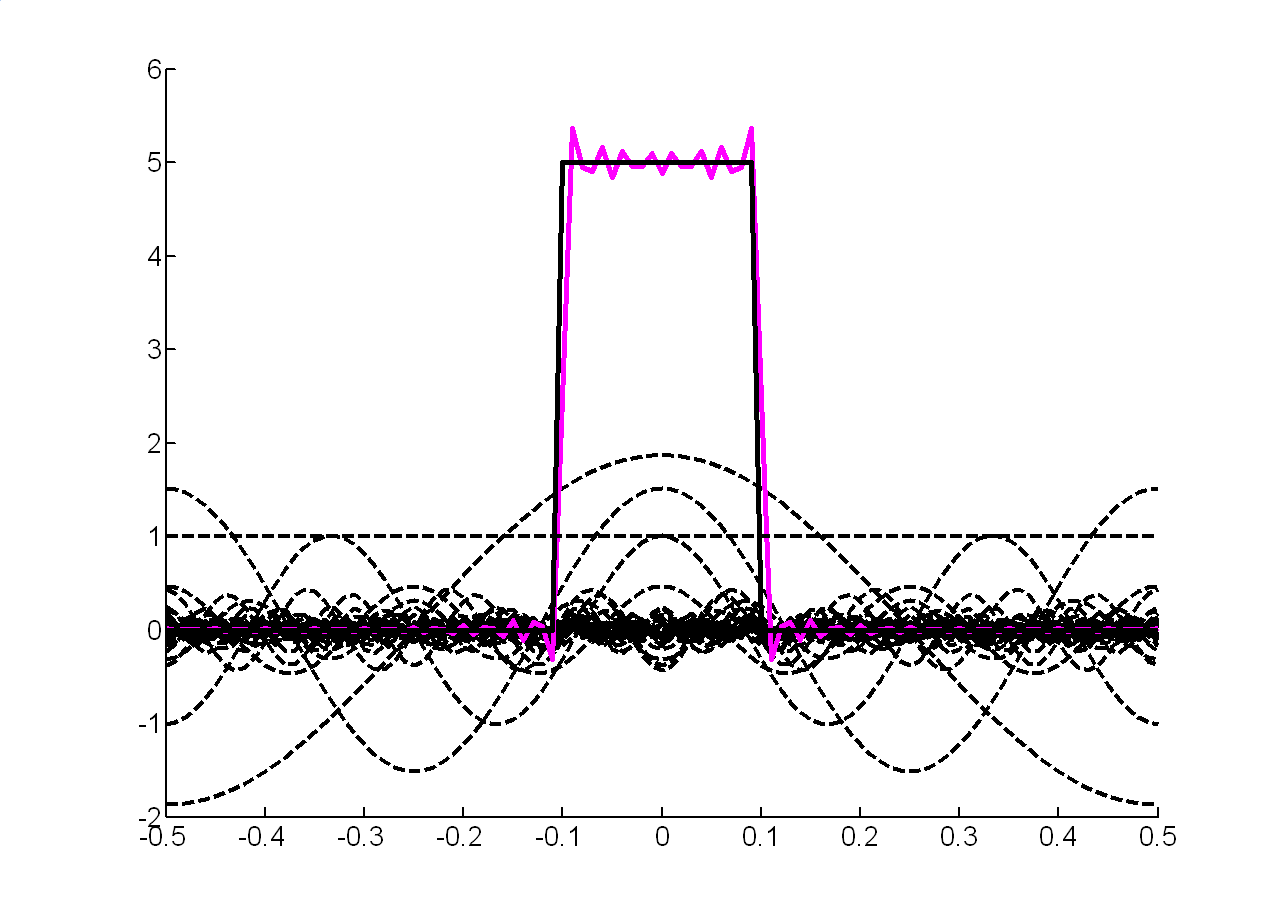
З урахуванням перших п'яти гармонік для отримуємо:
|
|
|
|
а) |
б) |
|
|
в) |
г) |
Рисунок 1.9 - Відновлений сигнал |
|
Приклад 1.2.
Розрахувати спектри амплітуд і фаз
періодичної послідовності пилкоподібних
імпульсів, тривалістю
![]() ,
амплітудою U0
і періодом T (рис.
1.10):
,
амплітудою U0
і періодом T (рис.
1.10):
|
|
|
|
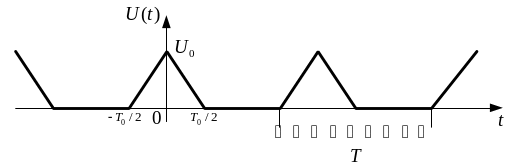
Рисунок 1.10 - Періодична послідовність пилкоподібних імпульсів |
|
Пилкоподібний сигнал (рис. 1.10) є парною функцією, тому розкладаючи його до ряду Фур'є отримуємо:
|
|
|
|
|
|
|
|
|
|
Таким чином, маємо:
|
|
Остаточно можемо записати:
|
|
Спектр цього сигналу є
речовинним і позитивним при будь-яких
значеннях
![]() ,
тобто на будь-якій частоті. Таким чином,
фазочастотний спектр має значення
.
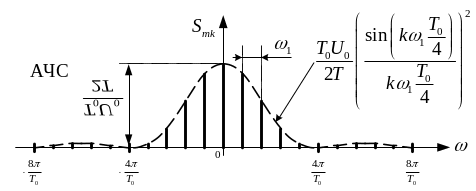
Амплітудно-частотний спектр наведено
на рис.1.11.
,
тобто на будь-якій частоті. Таким чином,
фазочастотний спектр має значення
.
Амплітудно-частотний спектр наведено
на рис.1.11.
|
Рисунок 1.11 - Амплітудно-частотний спектр послідовності пилкоподібних імпульсів |
При урахуванні перших п'яти
гармонік для
![]() отримуємо:
отримуємо:
|
|
|
|
а) |
б) |
Рисунок 1.12 - Відновлений сигнал |
|
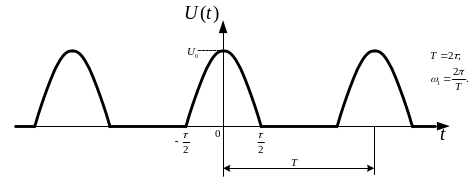
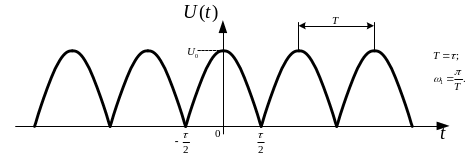
Приклад 1.3. Розрахувати спектри амплітуд і фаз періодичної послідовності косинусоїдальних імпульсів (рис. 1.13):
|
|
|
а) |
|
б) |
Рисунок 1.13 - Періодична послідовність косинусоїдальних імпульсів |
Комплексна амплітуда дорівнює
|
|
При
![]() (
) отримаємо:
(
) отримаємо:
|
|
Очевидно, що
|
|
тому можемо записати:
|
|
З урахуванням (1.5) отримуємо:
|
|
де
![]() при непарних
при непарних
![]() (
(![]() ) і
) і
![]() при парних
(
при парних
(![]() ), отже,
), отже,
![]() ,
тому можемо записати:
,
тому можемо записати:
|
|
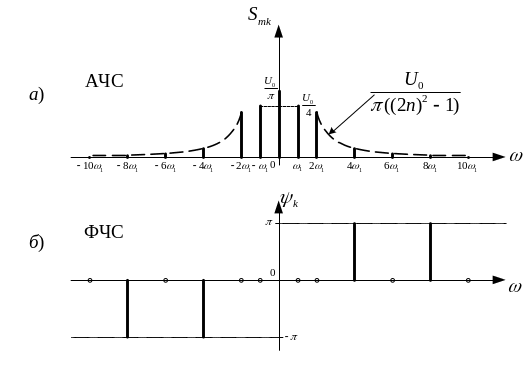
АЧС і ФЧС показано на рис.1.14.
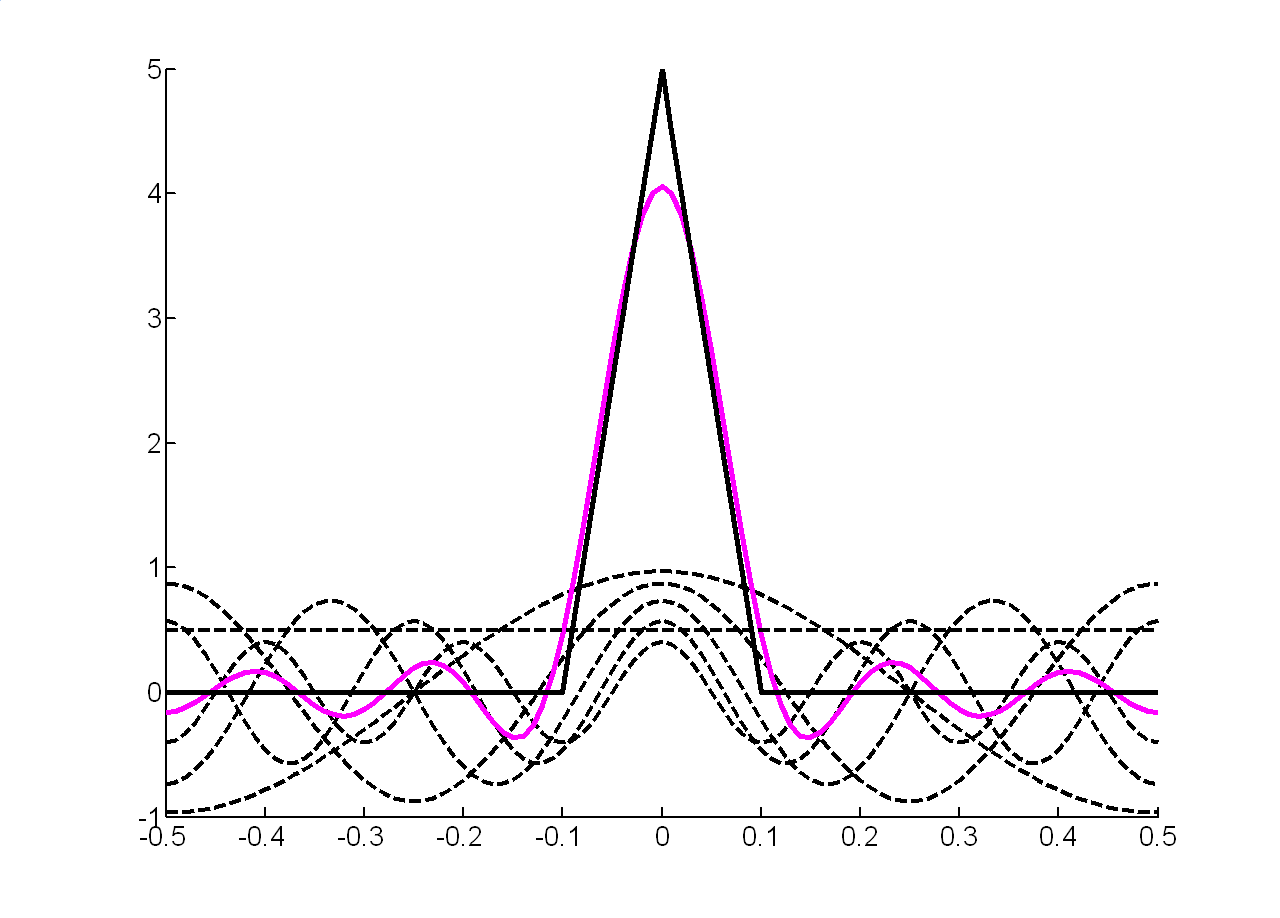
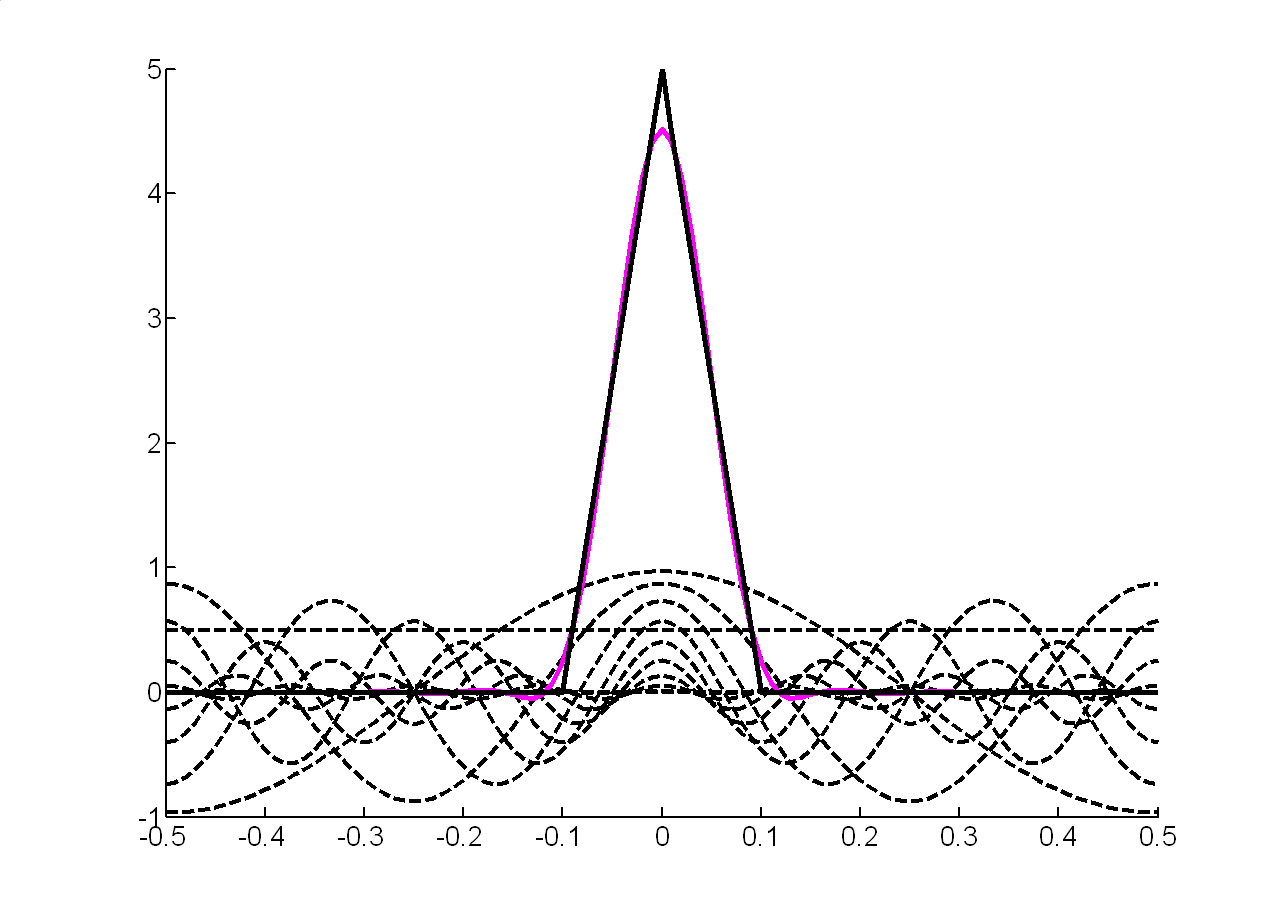
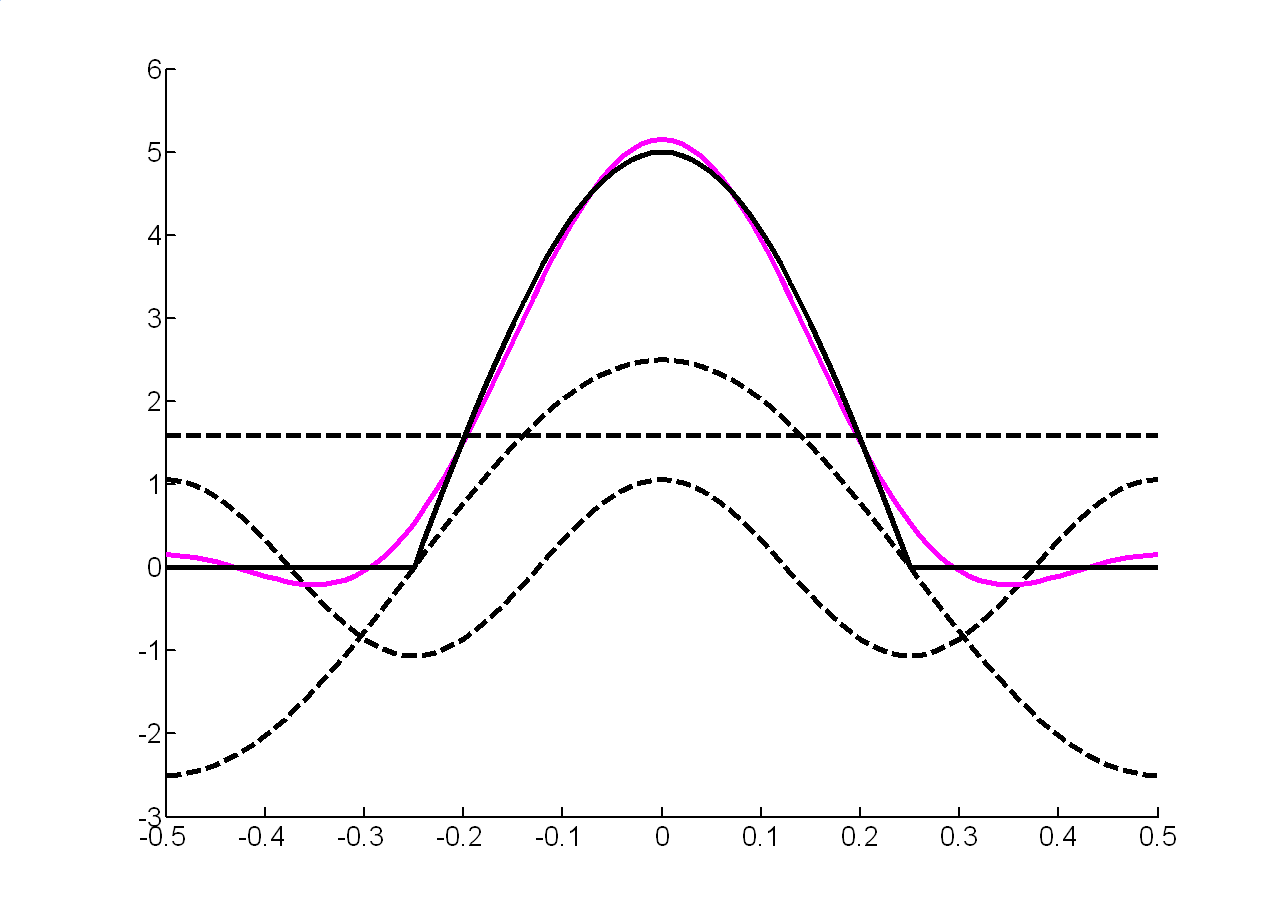
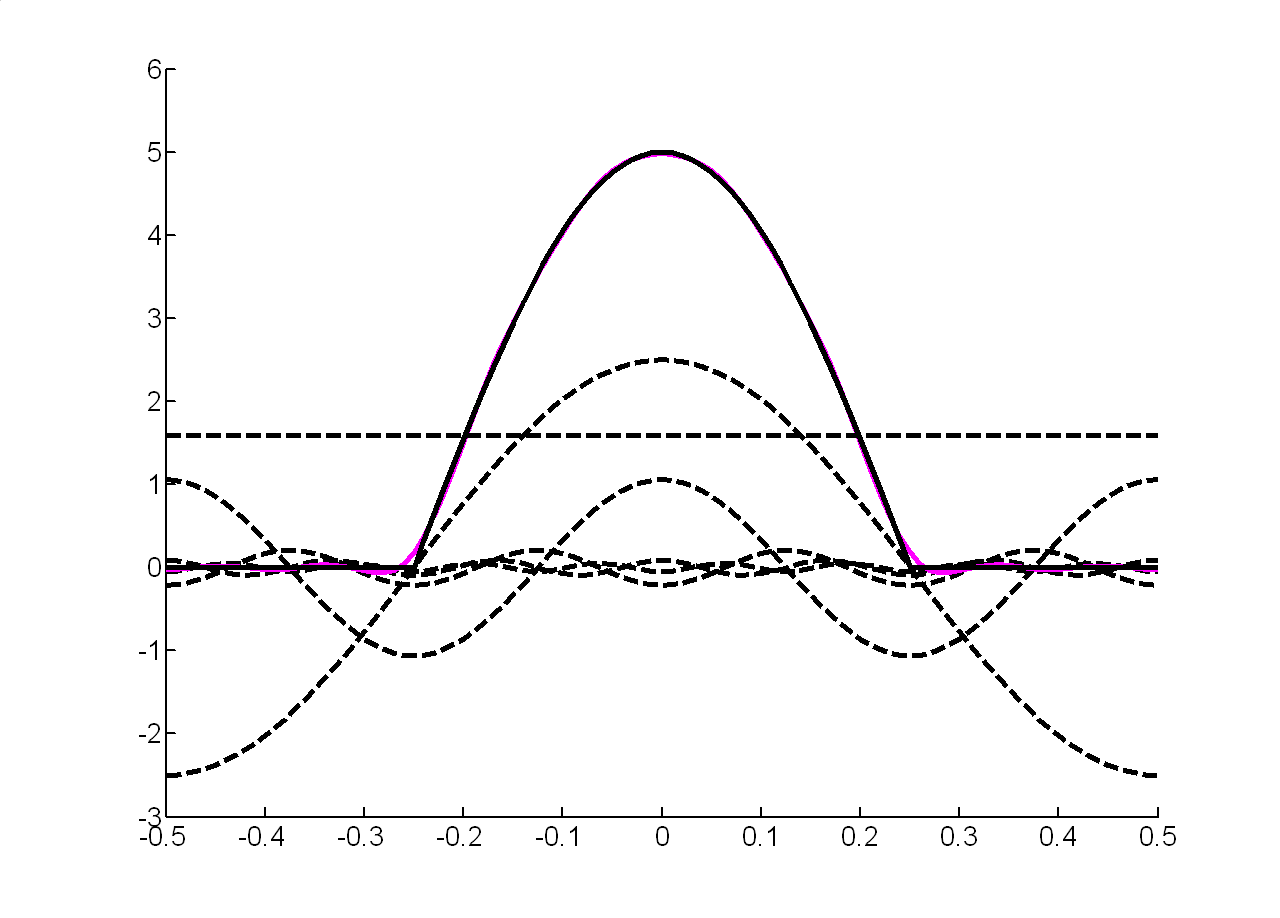
При урахуванні перших п'яти гармонік отримаємо:
|
|
|
Рисунок 1.14 - АЧС і ФЧС послідовності косинусоїдальних імпульсів |
|
|
а) |
б) |
Рис.1.15 Відновлений сигнал |
|
При
![]() (
(![]() ) отримаємо
) отримаємо
|
|
Тому що
|
|
то можемо записати:
|
|
Таким чином, спектр амплітуд містить тільки парні гармоніки:
|
|
Використовуючи (1.5) можемо записати:
|
|
де при непарних ( ) і при парних ( ), отже, , тому можемо записати:
|
|


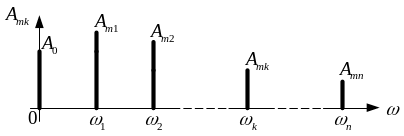
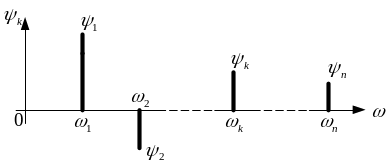
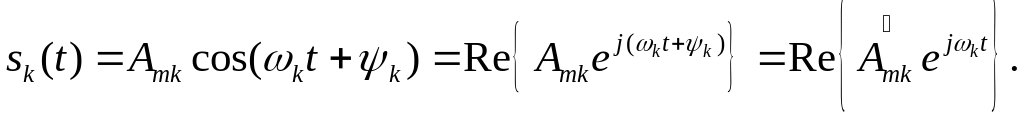
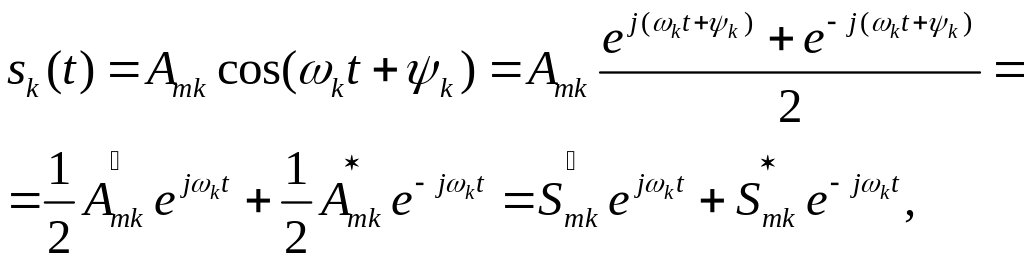
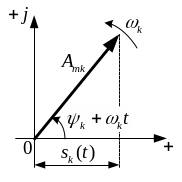
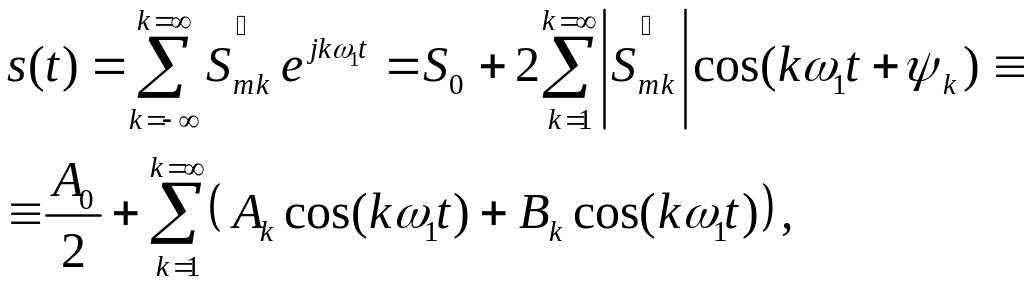
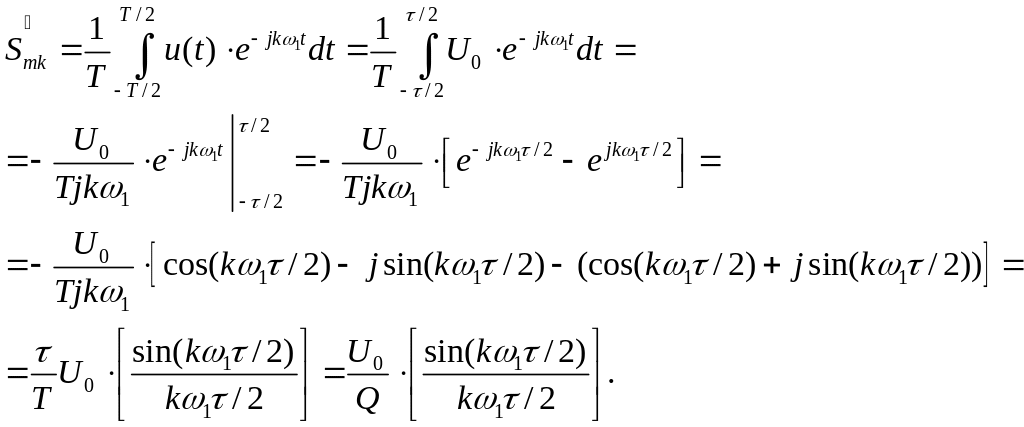
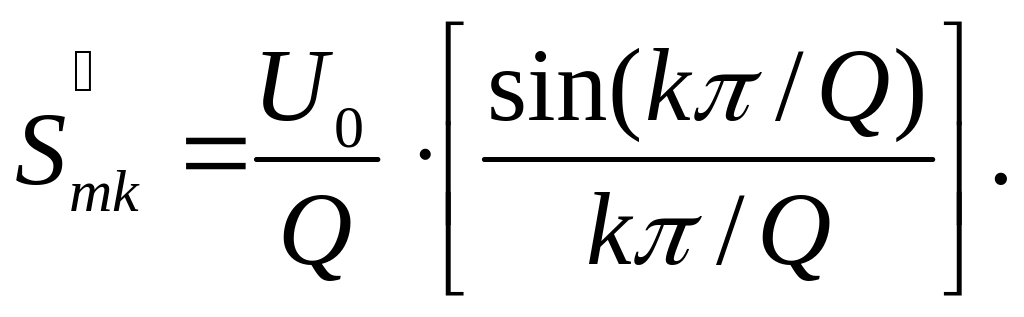
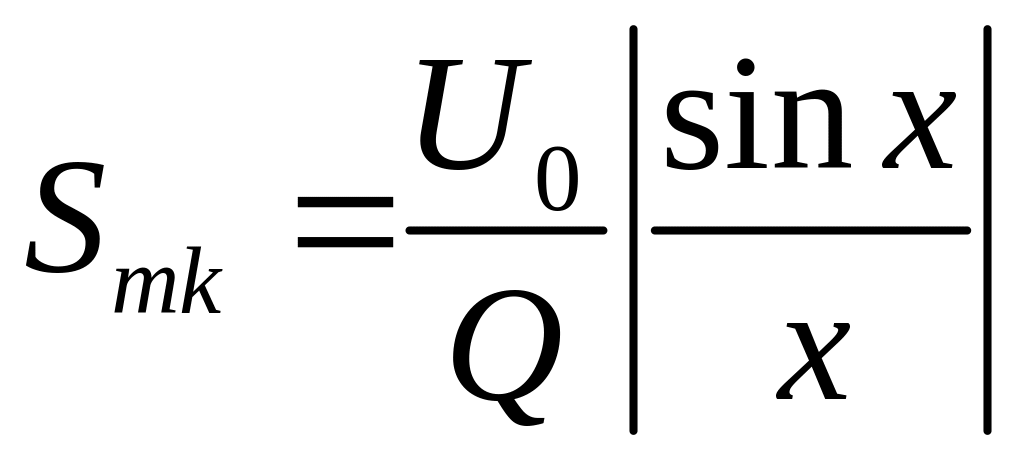 ,
,
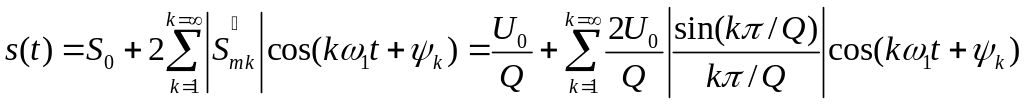 ,
,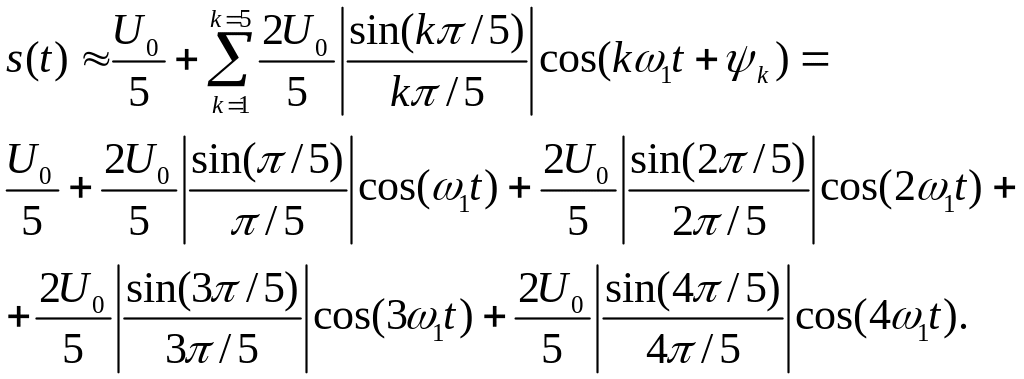
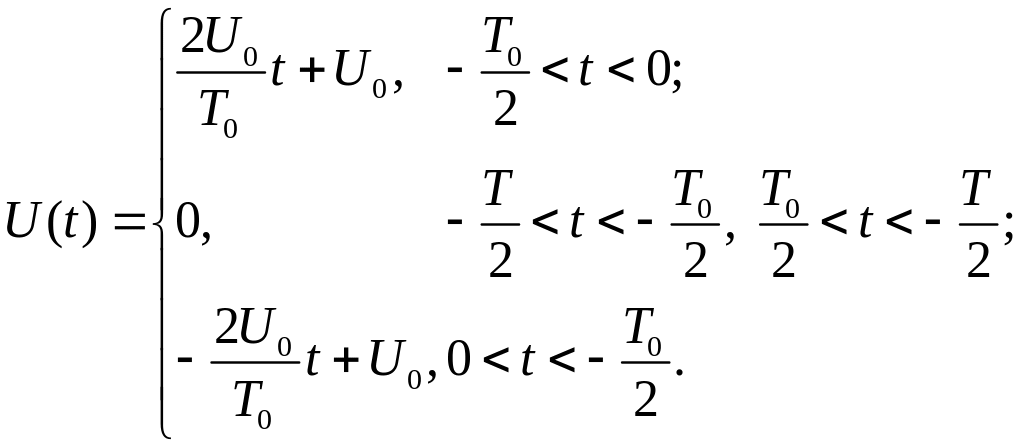
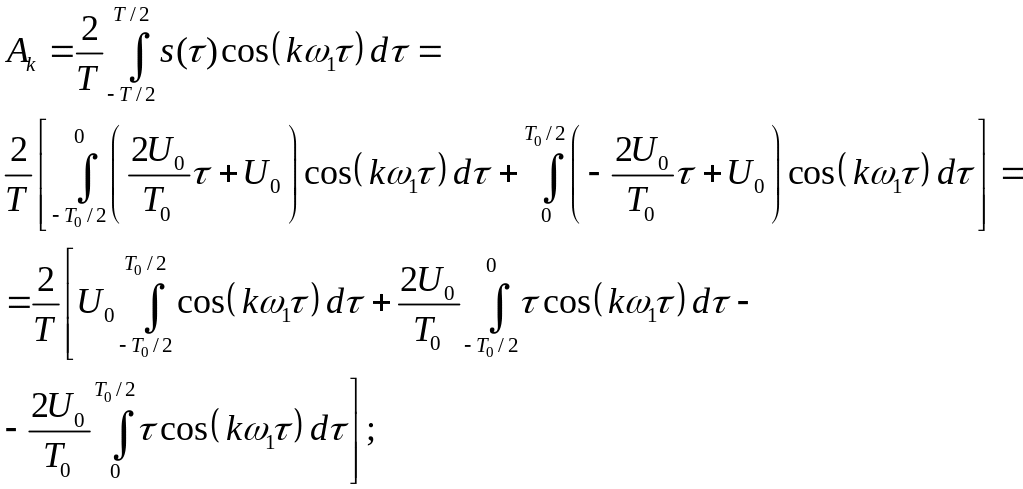
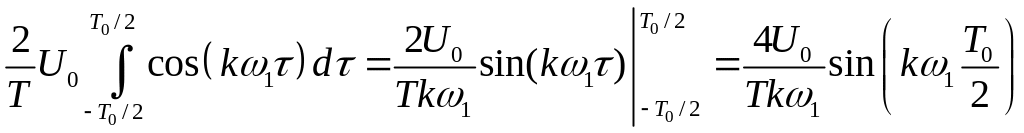 ;
;
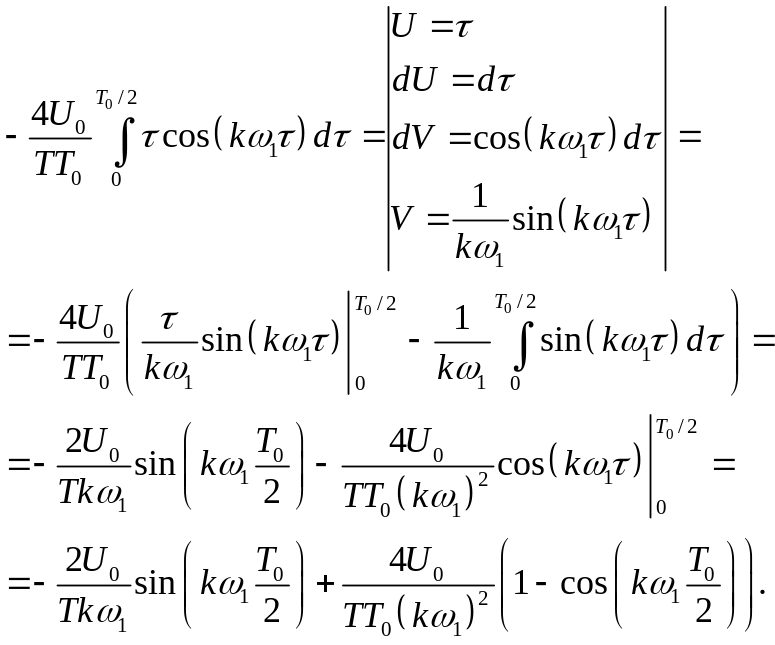
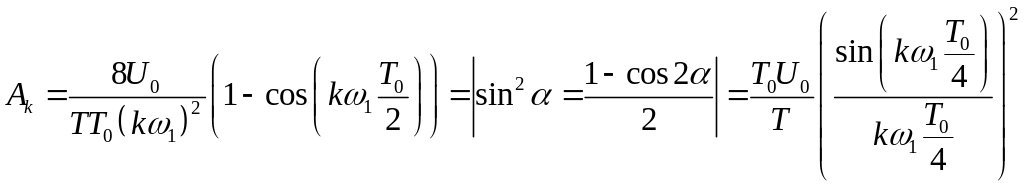 .
.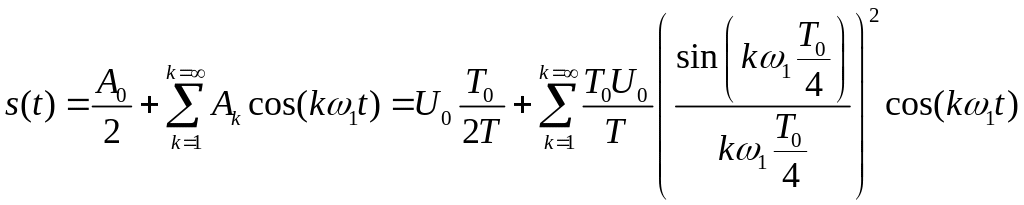 .
.
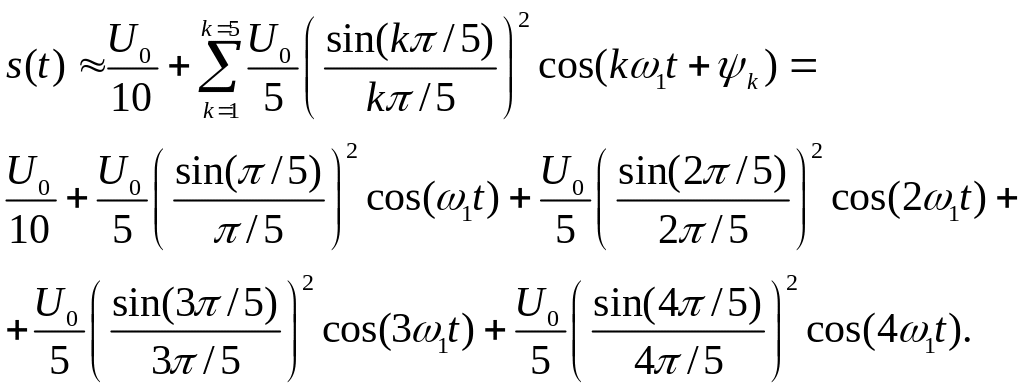
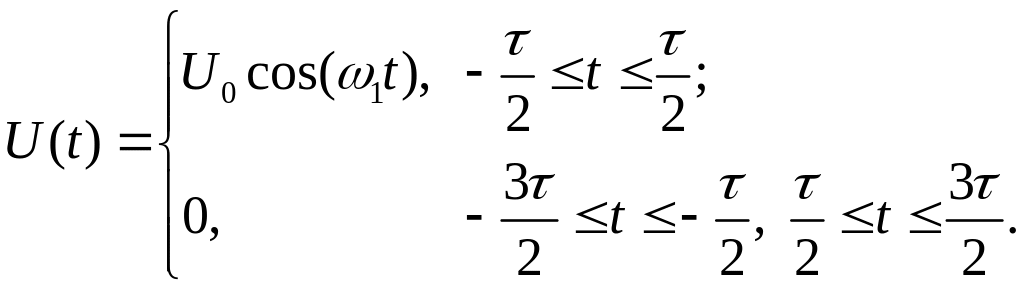
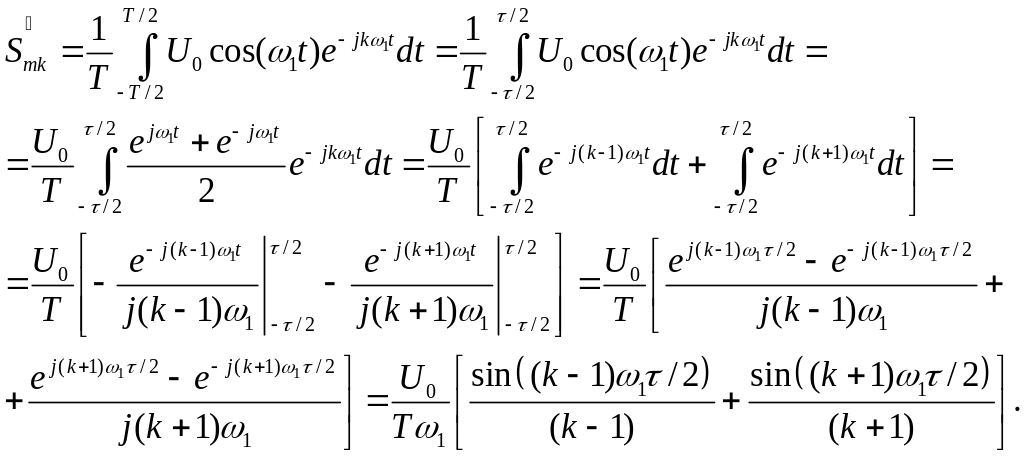
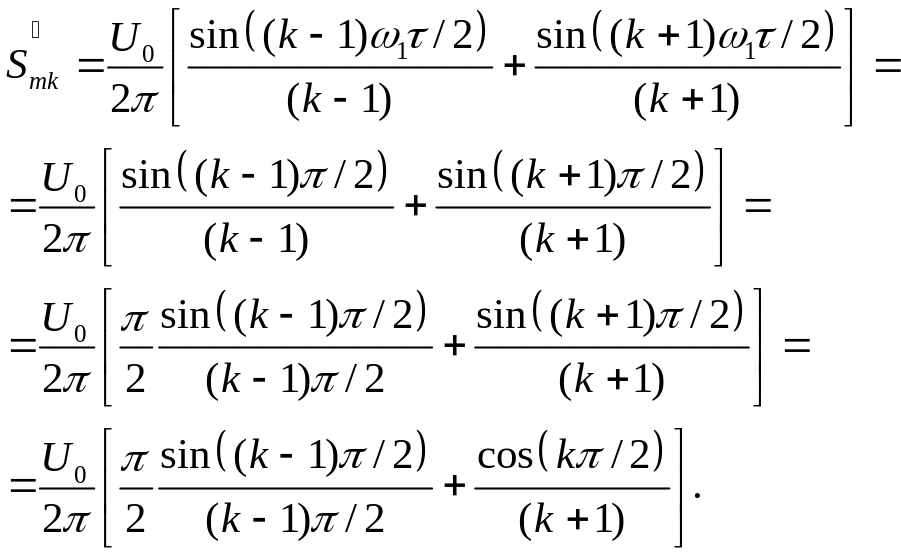
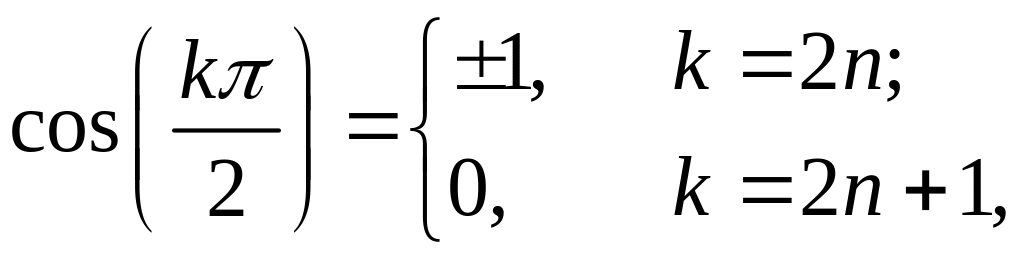

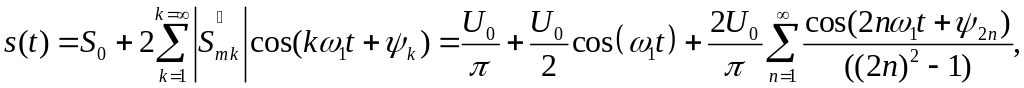
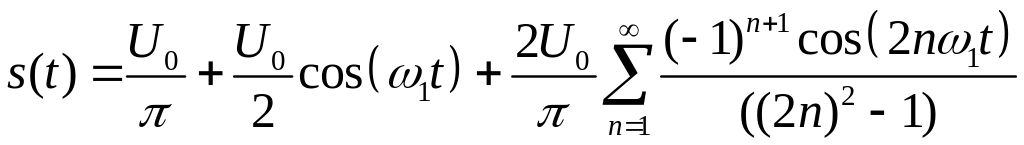 .
.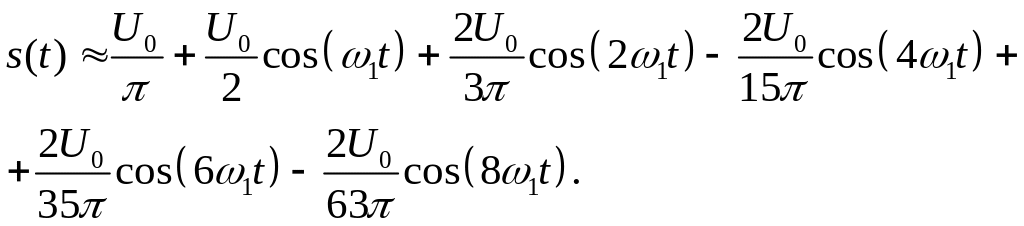
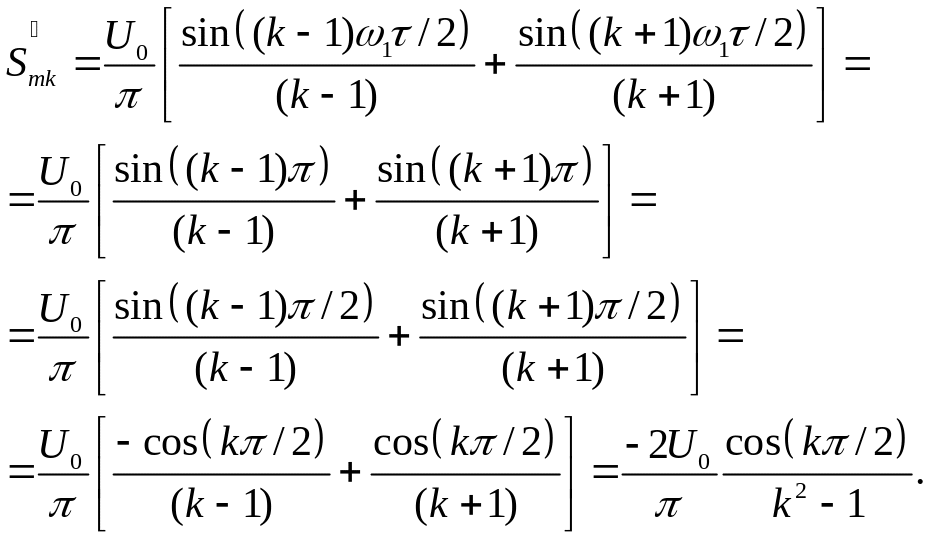
 .
.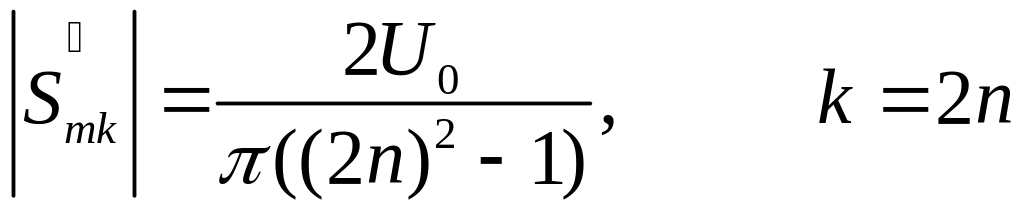 .
.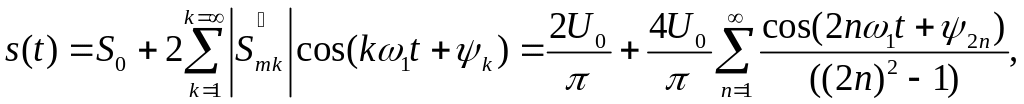
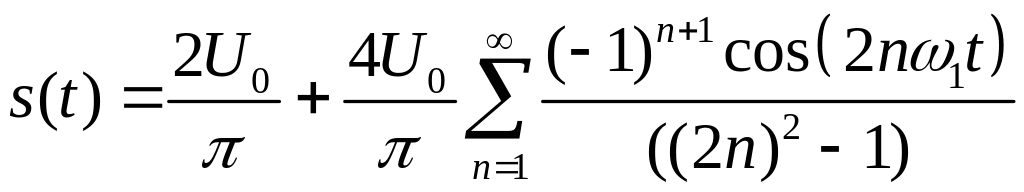 .
.