3.4 Контрольні запитання і завдання

1. Які труднощі виникають при використанні -вимірної щільності розподілу ймовірностей випадкового процесу для аналізу систем передачі інформації?

2. Якими усередненими характеристиками описуються звичайно випадкові процеси?

3. Що розуміють під математичним очікуванням і дисперсією випадкового процесу?

4. Що розуміють під кореляційною функцією випадкового процесу?

5. Що розуміють під стаціонарністю випадкового процесу в широкому та вузькому сенсах?

6. Які основні властивості має кореляційна функція стаціонарного процесу?

7. Який випадковий процес називають білим шумом?

8. Якою є кореляційна функція білого шуму?

9. Що розуміють під ефективною шириною спектру випадкового процесу?

10. Який зв'язок існує між інтервалом кореляції та ефективною шириною спектру випадкового процесу?

Практичне заняття №4 ентропія та її властивості

4.1 Мета заняття

Метою заняття є ознайомлення студентів з ентропійними характеристиками, що застосовуються у системах дискретної обробки інформації

4.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,7,9].

Методи оцінки кількості інформації, насамперед, пов’язані з її характером. до її змісту. У цей час існують три основні теорії, де поняття змістовного характеру інформації розглядається з різних позицій.

Статистична теорія оцінює інформацію з погляду міри невизначеності, яка зменшується при одержанні інформації. Як правило, вона не торкається змісту переданої інформації, тобто її систематичного змісту. У статистичній теорії основна увага звертається на розподіл ймовірностей окремих квантів інформації та побудову на його основі деяких узагальнених характеристик, що дозволяють оцінити кількість інформації в потрібному кванті.

Інший підхід використовують у семантичній теорії, що враховує в основному цінність та корисність і тим самим допомагає пов'язати ці характеристики з ефективністю інформаційної системи.

Нарешті, структурна теорія розглядає структуру побудови окремих інформаційних масивів, при цьому за одиницю інформації приймається деякі елементарні структурні одиниці (квант) і кількість інформації оцінюється підрахунком квантів в інформаційному масиві.

Вибір одиниці інформації в цей час є досить актуальною задачею.

Розглянемо дискретне джерело інформації, що може в кожний момент часу випадковим чином прийняти один з кінцевої множини можливих станів. Воно характеризується ансамблем , тобто повною сукупністю станів з ймовірностями їхньої появи, що складають у сумі одиницю:

,	(4.1)
.	(4.2)

Як міру невизначеності для джерела зі станами з однаковими ймовірностями, Хартлі в 1928 р. запропонував використовувати логарифм числа таких станів:

.

(4.3)

Основа логарифма визначає масштаб або одиницю невизначеності. При використанні десяткових логарифмів кількість інформації та ентропію визначають в десяткових одиницях - дітах. При використанні двійкових логарифмів кількість інформації та ентропію вимірюють у двійкових одиницях - бітах. Нарешті, при використанні натуральних логарифмів одиницею виміру є натуральна одиниця - ніт.

Приклад 4.1. Оцінити мінімальне число зважувань, яке необхідно зробити на рівноплечих вагах, щоб серед 27 монет знайти одну фальшиву (більш важку).

Рішення.

Загальна невизначеність ансамблю відповідно до формули (4.3) становить біт.

Одне зважування здатне прояснити невизначеність ансамблю , який нараховує три можливих результати. Його невизначеність дорівнює битка.

, тому для визначення фальшивої монети достатньо трьох зважувань.

Міра невизначеності вибору дискретним джерелом стану з ансамблю при різних ймовірностях станів була запропонована Шеноном – ентропія дискретного джерела інформації або ентропія кінцевого ансамблю:

,

(4.4)

де – довільне позитивне число.

Ентропія дискретних повідомлень має наступні властивості:

1. Ентропія є величина речовинна, обмежена та ненегативна. Ця властивість відповідає формулі (4.4), якщо врахувати, що ймовірності станів приймають значення з інтервалу .

2. Ентропія детермінованих повідомлень дорівнює нулю. Дійсно, якщо заздалегідь відомо, яке буде подія (наприклад ), то ймовірність цієї події дорівнює одиниці, а інших - нулю, тобто .

3. Ентропія максимальна, якщо всі події мають однакову ймовірність, тобто:

.

(4.5)

У цьому випадку ентропія обчислюється за формулою Хартлі (4.3).

4. Ентропія об'єднання кількох джерел дорівнює сумі ентропій вихідних джерел:

.

(4.6)

Приклад 4.2. Визначити ентропії двох дискретних джерел інформації:

и.

Рішення.

біта.

При оцінці невизначеності вибору часто необхідно враховувати статистичні зв'язки, які в більшості випадків мають місце між станами двох і більше джерел, які об'єднуються у рамках однієї системи, так і між станами, які послідовно приймає одне джерело.

Визначимо ентропію об'єднання двох статистично пов'язаних ансамблів та . Об'єднання ансамблів характеризується матрицею ймовірностей усіх можливих комбінацій станів ансамблю та станів ансамблю :

.

Суми елементів стовпців та рядків цієї матриці визначають інформацію для ансамблів й вихідних джерел:

, .

Імовірності спільної реалізації взаємозалежних станів і можна визначити через умовні ймовірності або відповідно до того, які стани прийняти за причину, а які за наслідок:

.

(4.7)

де – імовірність реалізації стану ансамблю за умови, що реалізувався стан ансамблю .

Отже:

.

Частковою умовною ентропією ансамблю називають суму , яка характеризує невизначеність, що доводиться на один стан ансамблю за умови, що реалізувався конкретний стан ансамблю .

.

(4.8)

Величину називають повною умовної або просто умовною ентропією ансамблю стосовно ансамблю .

.

(4.9)

Таким чином, ентропія двох ансамблів дорівнює сумі безумовної ентропії одного ансамблю й умовної ентропії іншого щодо першого.

Основні властивості умовної ентропії:

1. .

2. .

3. .

Графічно це відповідає діаграмам Вінера, що наведені на рис.4.1.

Рис.4.1 - Діаграми Вінера

Приклад 4.3. Визначити ентропії , , , , для дискретного джерела інформації, заданого ансамблем:

.

Рішення.

Визначимо безумовні ймовірності кожної системи як суму рядків і стовпців:

; ; ;

; ; ;

біт.

Визначимо умовні ймовірності:

;

;

; ; ;

; ; ;

; ; .

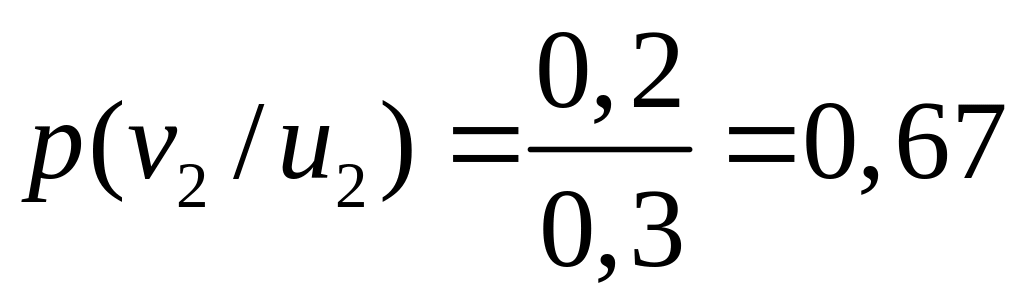Таким чином,

біт.

Виконуємо перевірку:

біт.

Приклад 4.4. Ентропії двох залежних джерел дорівнюють:  біт,  біт. Визначити, у яких межах буде змінюватися умовна ентропія при зміні умовної ентропії в максимальних межах.

Рішення.

Умовна ентропія максимальна при відсутності взаємозв'язку між джерелами:

біт.

При збільшенні взаємозв'язку умовна ентропія зменшується до значення  біт. При цьому .

Приклад 4.5. Оцінити ентропію системи, яка описується дискретною випадковою величиною з наступним рядом розподілу:

; .

Рішення.

біт.

Приклад 4.6. Визначити ентропію повідомлення з п'яти символів, якщо загальне число букв дорівнює 32, і всі повідомлення мають однакову ймовірність.

Рішення.

Загальне число п’ятисимвольних повідомлень: .

 біт.

Передача інформації ініціюється або самим джерелом інформації, або здійснюється по запиту. Вона має за ціль усунути невизначеність щодо послідовності станів, які реалізовано деяким джерелом інформації.

У реальних умовах передача інформації відбувається за умов впливу перешкод. Перешкоди спотворюють повідомлення, тобто буде мати місце неповна вірогідність передачі.

Внаслідок можливої відмінності прийнятих повідомлень від переданих при оцінці кількості переданої інформації будемо розглядати систему переданих повідомлень і прийнятих . Нехай .

Прийняті повідомлення характеризуються сукупністю значень . Перешкоди мають випадковий характер, тому при прийманні деякого повідомлення не можна точно визначити, яке повідомлення було передано. Можна лише говорити про умовну ймовірність , яка визначає ймовірність передачі повідомлень за умови, що буде прийняте повідомлення .

Оцінимо кількість інформації, яка міститься в одному із прийнятих повідомлень про одне з переданих повідомлень .

Умовна ймовірність свідчить про те, що існує невизначеність у повідомленні щодо повідомлення . Ця невизначеність може бути оцінена умовною ентропією:

.

(4.10)

Таким чином, через перешкоди початкова апріорна ентропія повідомлення визначається кількісно формулою

,

(4.11)

знімається при одержанні повідомлення не повністю, а лише зменшується до значення . Кількість інформації в цьому випадку буде дорівнювати знятої частини невизначеності:

.

(4.12)

Це співвідношення виражає кількість інформації, яка міститься в прийнятому повідомленні щодо переданого – часткова кількість інформації, яка міститься в повідомленні відносно .

Середня кількість інформації про усі , яка міститься в одному прийнятому повідомленні :

.

(4.13)

Кількість інформації у всій сукупності прийнятих повідомлень щодо всієї сукупності переданих :

Відомо, що , то .

Отже,

Таким чином, кількість інформації, яка одержується при передачі з перешкодами, дорівнює різниці безумовної ентропії , яка характеризує початкову невизначеність повідомлення, та умовної ентропії , яка характеризує залишкову невизначеність повідомлення.

Приклад 4.7.. Визначити середню кількість інформації, яку отримано при передачі повідомлення по каналу, який задано матрицею спільних ймовірностей:

.

Рішення.

;

;

біт.

Основні властивості кількості інформації:

1. Хоча часткова кількість інформації може бути менше нуля, кількість інформації - величина ненегативна

.

(4.14)

2. При відсутності статистичного зв'язку між випадковими величинами й 

.

(4.15)

Отже,

,

(4.16)

тобто прийняті елементи повідомлення не несуть ніякої інформації щодо переданих даних.

3. Кількість інформації у відносно дорівнює кількості інформації відносно .

.

(4.16)

4. При відсутності перешкод умовна ентропія дорівнює нулю й кількість інформації збігається з ентропією джерела.

(4.17)