3.3 Задачі для самостійної роботи

3.3.1 Знайти кореляційну функцію для процесу зі спектральною щільністю у вигляді функції - (рис. 3.14).

Рис.3.14 Спектральна щільність процесу

3.3.2 Білий шум зі спектральною щільністю проходить через підсилювач із частотною характеристикою у формі гаусової кривої (рис.3.15). . Знайти кореляційну функцію й спектральну щільність вихідного сигналу
	Рис. 3.15 Спектральна щільність процесу

3.3.3 Кореляційна функція випадкового процесу задана співвідношенням , де (рис.3.16). Знайти спектральну щільність випадкового процесу.
	Рис. 3.16 Кореляційна функція випадкового процесу

3.3.4 Знайти інтервал кореляції стаціонарного випадкового процесу з функцією кореляції .

3.3.5 Стаціонарний випадковий процес має ефективну ширину спектра, рівну 1,5 Мгц. Максимальне значення однобічного спектра потужності становить . Визначити дисперсію даного процесу.

3.3.6 Знайти середнє значення й дисперсію огинаючої вузькосмугового нормального випадкового процесу з функцією кореляції .

3.3.7 Вузькосмуговий нормальний випадковий процес має функцію кореляції . Знайти функцію кореляції й спектральну щільність огинаючої цього процесу.

3.3.8 Вузькосмуговий нормальний випадковий процес має функцію кореляції . Довести, що квадрат огинаючої цього процесу має функцію кореляції .

3.3.9 Вузькосмуговий нормальний випадковий процес характеризується функцією кореляції . Знайти одномірну щільність імовірності миттєвої частоти даного процесу.

3.3.10 Визначити спектральну щільність стаціонарного випадкового процесу , який описується функцією кореляції

3.3.11 Знайти функцію кореляції стаціонарного випадкового процесу, що має спектральну щільність .

3.3.12 Визначити спектральну щільність випадкового процесу з лінійно убутною нормованою функцією автокореляції

де .

3.3.13 Знайти кореляційну функцію й дисперсію стаціонарного випадкового процесу зі спектральною щільністю гаусова виду .

3.3.14 Знайти кореляційну функцію й дисперсію стаціонарного випадкового процесу з обмеженою спектральною щільністю низькочастотного виду

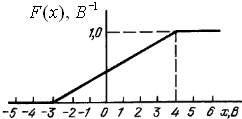
3.3.15 Згідно з заданою графічно функцією розподілу стаціонарного випадкового коливання (рис. 3.18) визначити щільність імовірності й зобразити зразковий вид реалізації даного процесу.
	Рис. 3.18 Функція розподілу

3.3.16 Опір ланцюга (лінійний елемент) і струм - некорельовані стаціонарні випадкові коливання. Визначити середнє значення електрорушійної сили , що створює струм у ланцюзі, якщо відомо, що  Ом, а  А.

3.3.17 Згідно з заданою щільністю ймовірності стаціонарного випадкового процесу (електричного струму) , визначити коефіцієнт , функцію розподілу та імовірність перебування значення в інтервалі . Побудувати графіки й для випадку  А^-1.

3.3.18 Визначити математичне очікування, дисперсію, середній квадрат і середньоквадратичне значення стаціонарної випадкової напруги, який задано одномірною щільністю ймовірності

3.3.19 Функція розподілу стаціонарної випадкової напруги має вигляд

Визначити математичне очікування, дисперсію й середній квадрат цього процесу. Пояснити фізичний сенс цих параметрів.

3.3.20 Напруга на виході вимірювального підсилювача є нормальним стаціонарним випадковим процесом з математичним очікуванням  мВ і дисперсією  В². Визначити ймовірність того, що миттєве значення напруги не перевищить за модулем 150 мВ.

3.3.21 Кореляційні функції трьох випадкових процесів дорівнюють: а)  ; б)  ; в)  . Визначити інтервал кореляції , де - нормована кореляційна функція процесу.

3.3.22 Визначити спектральні щільності середньої потужності стаціонарних випадкових коливань по відомим кореляційним: а)  ; б)  . Побудувати графіки отриманих .

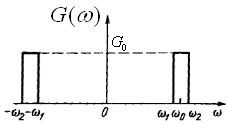
3.3.23 Згідно з заданою графічно спектральній щільності середньої потужності (рис. 3.19) визначити кореляційну функцію стаціонарного випадкового процесу.
	Рис. 3.19 Спектральна щільність середньої потужності процесу

3.3.24 Визначити ефективну ширину спектра стаціонарних процесів за заданими кореляційними функціями: а)  ; б)  ; в)  .

3.3.25 Визначити кореляційну функцію та дисперсію стаціонарного випадкового процесу, що має спектральну щільність середньої потужності .