2.4 Контрольні запитання і завдання

1. За яких умов неперіодична функція може бути представлена інтегралом Фур'є?

2. Яким чином можна отримати спектр неперіодичного сигналу безпосередньо зі спектру відповідного періодичного сигналу?

3. Як можна енергетично визначити спектр неперіодичного сигналу?

4. Що є практичною шириною спектра неперіодичного сигналу? Які критерії використовують для вибору практичної ширини спектру сигналу?

5. Як спектр неперіодичного сигналу відрізняється від спектру періодичного сигналу?

ПРАКТИЧНЕ ЗАНЯТТЯ №3

МАТЕМАТИЧНІ МОДЕЛІ ВИПАДКОВИХ СИГНАЛІВ

3.1 Мета заняття

Метою заняття є ознайомлення студентів з математичними моделями випадкових сигналів.

3.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,8].

3.2.1 Випадкові сигнали та їх імовірнісні характеристики. У реальних умовах більшість сигналів має випадковий характер, внаслідок чого одержувач заздалегідь не може передбачати, яким буде переданий сигнал.

Однак не можна також затверджувати, що приймальна сторона не має у розпорядженні ніяких попередніх (апріорних) даних про сигнали. По-перше, попередньо часто є відомою вся множина (ансамбль) можливих сигналів. По-друге, як правило, заздалегідь відомі значення очікуваної ймовірності сигналів із загального ансамблю сигналів. Наприклад, при передачі тексту відомо, які букви, а також сполучення букв і сполучення слів використовуються при передачі частіше і які рідше.

Таким чином, попередні відомості, які ми маємо про сигнали, носять статистичний характер. Тому для дослідження проходження сигналів через інформаційні системи варто застосовувати статистичні методи.

Доцільність застосування статистичних методів обумовлена ще й тим, що на сигнал впливають перешкоди, що є, як правило, невідомими функціями часу. Основним змістом задачі прийому сигналів на фоні перешкод є найбільш повне добування інформації із сигналу. Успішного рішення цієї задачі можна досягти тільки на основі використання статистичних методів прийому.

Нарешті, доцільність використання статистичних методів викликана ще й тим, що характеристики систем, по яких проходять сигнали, під впливом різноманітних зовнішніх і внутрішніх факторів можуть змінюватися випадковим образом.

Рис.3.1 Випадкові процеси	Рис.3.2 Нормальний закон розподілу

Процес, що описується за допомогою випадкової функції часу, називається випадковим процесом. Іноді замість терміна «Випадковий процес» застосовують у тому ж сенсі терміни «Стохастичний процес» або «Імовірнісний процес».

Конкретний вигляд, який приймає випадковий процес за результатами реєстраційного експерименту, називається реалізацією процесу. Окремі спостереження випадкового процесу в однотипних системах за однакових умов реєстрації дають різні реалізації випадкового процесу (рис. 3.1). Вигляд функції випадковим чином змінюється від однієї реалізації до іншої. Сукупність реалізацій випадкового процесу, отриманих у результаті реєстрації, називається ансамблем реалізацій випадкового процесу .

Величина -ї реалізації випадкового процесу в певний момент часу (наприклад, ) називається вибіркою випадкового процесу . Сукупність значень вибірок у певний момент часу (наприклад, ) утворює випадкову величину .

Імовірність того, що в певний момент часу величина перебуває в інтервалі між і , дорівнює

(3.1)

де - одномірна щільність імовірності або одномірна функція розподілу випадкового процесу .

Щільність імовірності є в загальному випадку функцією часу, тому що залежить від , є похідною від інтегральної функції розподілу

На рис. 3.2 наведено графік нормального закону розподілу щільності ймовірності випадкової величини в певний момент часу , який найбільш часто зустрічається на практиці.

Математичний опис цього закону має вигляд

(3.2)

де й — математичне очікування й середньоквадратичне відхилення випадкової величини .

Заштрихована на рис. 3.2. площа під кривою розподілу дорівнює ймовірності знаходження в інтервалі між і

.

(3.3)

Для будь-якого закону розподілу щільності ймовірності є чинною рівність

(3.4)

Одновимірний закон розподілу щільності ймовірностей є найпростішою статистичною характеристикою випадкового процесу. Він дає уявлення про процес лише в окремі, фіксовані моменти часу, характеризує процес статично й не відображує динаміку його розвитку.

Для більш повної характеристики випадкового процесу необхідно знати характер зв'язку між імовірними значеннями випадкової функції при двох довільних моментах часу й . Цей зв'язок виражається через двовимірну щільність імовірності і формулюється в такий спосіб: імовірність знаходження кожної з функцій , що входять у сукупність функцій , в інтервалі в момент часу й в інтервалі в момент часу .

(3.5)

де - двовимірна щільність імовірності або двовимірна функція розподілу випадкового процесу .

На рис. 3.3. наведено поверхню двовимірного нормального закону розподілу щільності ймовірності для випадкових величин з нульовим середнім значенням у моменти часу .

Міркуючи аналогічним образом, можна ввести поняття про тривимірну , а також про -мірну щільності імовірності випадкового процесу . Тоді ймовірність складної події, яка полягає в тім, що в момент часу функція перебуває в інтервалі в момент часу функція перебуває в інтервалі й т.д., у момент часу перебуває в інтервалі й т.д.,

	((3.6)

Рис.3.3 Двовимірний нормальний закон розподілу

Чим більше число , тим точніше -вимірна функція розподілу характеризує статистичні властивості випадкового процесу. Однак -вимірні функції розподілу можуть бути отримані за допомогою досить складної й трудомісткої обробки множини реалізацій випадкового процесу. При користуванні -вимірними функціями розподілу виникають істотні математичні труднощі. Тому на практиці частіше оперують кінцевим числом числових характеристик, які дають безумовно менш повну характеристику випадкового процесу, але достатню для рішення ряду важливих задач і, крім того, можуть бути отримані шляхом порівняно простої обробки реалізації випадкового процесу.

3.2.2 Числові характеристики випадкового процесу. Найпростішими моментними функціями, які в основному використовуються для характеристики випадкових процесів, є моменти розподілу перших двох порядків: математичне очікування, дисперсія та кореляційна функція випадкового процесу.

Математичне очікування (або перший момент одномірного закону розподілу) визначається за формулою

(3.7)

Фізично математичне очікування відповідає середньому значенню сукупності вибірок випадкового процесу (випадкової величини ) у певний момент часу .

Дисперсія (або другий центральний момент одномірного закону розподілу) - це математичне очікування квадрата відхилення величин від математичного очікування в певний момент часу , що визначається за формулою

(3.8)

Дисперсія виражає міру розсяглості значень випадкової величини біля математичного очікування, іншими словами - «ступінь випадковості» величини .

Квадратний корінь від дисперсії називають середньоквадратичним відхиленням випадкової величини.

Аналогічно можна знайти середнє значення квадрата випадкової величини :

(3.9)

Позитивний корінь цієї величини називається середньоквадратичним значенням .

Згідно з (3.8) можна встановити залежність між дисперсією й середньоквадратичним значенням випадкової величини:

.

З урахуванням того, що , можна отримати

,

(3.10)

тобто дисперсія дорівнює різниці квадратів середньоквадратичного значення й математичного очікування.

При дисперсія збігається із квадратом середньоквадратичного значення випадкової величини .

Математичне очікування, дисперсія та середньоквадратичне значення випадкової величини є в загальному випадку функціями часу. Вони характеризують траєкторію випадкового процесу в окремі моменти часу, але не враховують зв'язок між значеннями випадкового процесу в різні моменти часу. Цей зв'язок відображує кореляційна функція , яка дорівнює середньому значенню добутку значень випадкової функції в моменти часу й

.

(3.11)

Зв'язок між значеннями двох випадкових процесів і у моменти часу й відповідно відображує взаємна кореляційна функція , яка дорівнює середньому значенню добутку

.

(3.12)

Часто використовують нормовані автокореляційну й взаємну кореляційну функції (коефіцієнти кореляції), які визначаються за формулами:

;	(3.13)
.	(3.14)

Нормовані кореляційні функції зручні тим, що вони не перевершують одиниці за абсолютною величиною.

Математичне очікування, дисперсія, квадрат середньоквадратичного значення та кореляційна функція, які визначаються за формулами (3.7), (3.8) та (3.11) відповідно, отримують шляхом осереднення множини реалізацій випадкового процесу для фіксованих моментів часу. Осереднені характеристики можуть бути також отримані шляхом обробки однієї з реалізацій випадкового процесу на досить великому інтервалі часу.

Середнє за часом значення випадкового процесу визначається за формулою

(3.15)

де - реалізація випадкового процесу ; - час спостереження процесу.

За аналогією користуються поняттями середнього за часом значення від функції , від квадрата різниці та від добутку , які визначаються відповідно за формулами

	(3.16)
	(3.17)
	(3.18)

У загальному випадку для різних реалізацій випадкового процесу утворюються різні значення середнього за часом від , , та .

Якщо припустити, що відображує зміну напруги (або струму), то фізично (3.15) дорівнює потужності постійної складової, що розсіюється на опорі в 1 Ом. У зв'язку із цим вважають, що середнє за часом відповідає потужності постійної складової реалізації випадкового процесу .

За аналогією можна вважати, що (3.16) відображає повну середню потужність, а (3.17) - середню потужність «випадкової» складової процесу .

Якщо випадковий сигнал є дискретним, то числові характеристики визначаються за формулами

	(3.19)

де - апріорна ймовірність випадкової величини ; - спільна апріорна ймовірність величин і ; - число значень випадкової величини .

3.2.3 Стаціонарні випадкові процеси. В інформаційних системах дуже часто зустрічаються випадкові процеси, що відбуваються у часі приблизно однорідно. Ці процеси мають вигляд неперервних випадкових коливань біля деякого середнього значення, причому ні середнє значення, ні характер цих коливань не зазнають істотних змін у часі. Такі випадкові процеси називаються стаціонарними.

Прикладами стаціонарних випадкових процесів є шуми на виході електронних пристроїв, випадкові коливання в ланцюгах живлення та т.і.

У будь-якій динамічній системі випадковий процес починається з так званого «перехідного» процесу, а потім переходить у сталий режим, що з деяким наближенням можна вважати стаціонарним. Строго кажучи, стаціонарні процеси є нескінченними у часі, тобто не мають ані початку, ані кінця. Таких процесів практично не існує. Однак багато випадкових процесів на певних відрізках часу з певним наближенням можна вважати стаціонарними.

Відомо два поняття стаціонарності: стаціонарність у вузькому смислі та стаціонарність у широкому смислі.

Під стаціонарними процесами у вузькому смислі розуміють випадкові процеси, для яких функція розподілу щільності ймовірності довільного порядку не змінюється за будь-якого зсуву усієї групи моментів вздовж осі часу, тобто для будь-яких і :

.

(3.20)

З цього випливає, що для стаціонарних процесів:

а) одновимірна функція розподілу щільності ймовірності не залежить від часу, тобто

;

(3.21)

б) двовимірна функція розподілу щільності ймовірності залежить тільки від різниці часу , тобто

;

(3.22)

в) тривимірна функція розподілу щільності ймовірності залежить тільки від двох різниць часів і , тобто

і т.д.

(3.23)

Оскільки математичне очікування й дисперсія виражаються через одновимірну функцію розподілу щільності ймовірності, то на підставі слідства (а) можна затверджувати, що для стаціонарного процесу математичне очікування й дисперсія не залежать від часу. Внаслідок залежності двовимірної функції розподілу тільки від різниці часів , кореляційна функція стаціонарного процесу також залежить тільки від різниці часів .

Таким чином, для стаціонарних процесів

	(3.24)

На практиці найбільш часто зустрічаються випадкові процеси, для яких при виконанні умов (3.24) моменти вищих порядків залежать від часу. Тому поняття стаціонарності виявилося доцільним розширити, взявши за основу визначення стаціонарності умови (3.24).

У зв'язку з цим було запропоновано поняття стаціонарності в широкому сенсі, відповідно до якого стаціонарними процесами є такі випадкові процеси, математичне очікування й дисперсія яких не залежать від часу, а кореляційна функція залежить тільки від різниці часів .

Випадкові процеси, стаціонарні у вузькому смислі, будуть завжди стаціонарними в широкому смислі, але не навпаки.

Стаціонарні випадкові процеси за своєю природою простіші, ніж нестаціонарні, завдяки чому описуються більш простими характеристиками. Через те, що стаціонарні процеси зустрічаються на практиці дуже часто, набула широкого застосування спеціальна теорія стаціонарних випадкових процесів.

Властивості стаціонарного процесу багато в чому обумовлюються властивостями кореляційної функції, тому для вивчення стаціонарного процесу потрібно, у першу чергу, визначити властивості кореляційної функції.

3.2.4 Властивості кореляційної функції стаціонарного випадкового процесу. Визначимо, як поводиться кореляційна функція при необмеженому збільшенні різницевого часового інтервалу .

Зі збільшенням часового інтервалу залежність між величинами й слабшає. При ці величини стають незалежними. З урахуванням того, що математичне очікування добутку випадкових незалежних величин дорівнює добутку математичних очікувань співмножників і що для стаціонарного процесу математичне очікування не залежить від часу, отримаємо:

(3.25)

Таким чином, при необмеженому збільшенні аргументу кореляційна функція прагне до квадрату математичного очікування випадкового процесу.

Отже, при кореляційна функція дорівнює потужності постійної складової реалізації випадкового стаціонарного процесу.

При зменшенні часового інтервалу залежність між величинами та посилюється, а при отримаємо

(3.26)

Таким чином, при кореляційна функція дорівнює початковому моменту другого порядку функції . Фізично початковий момент другого порядку відображує, як відомо, повну середню потужність випадкового процесу.

Отже, дисперсія стаціонарного випадкового процесу

(3.27)

У силу незалежності функції розподілу щільності ймовірності стаціонарного випадкового процесу від початку відліку часу кореляційна функція є парною функцією , тобто

(3.28)

Можна показати, що кореляційна функція за абсолютним значенням є максимальною при . Дійсно, якщо розглянути математичне очікування квадрата суми або різниці величин і , то отримаємо

Середнє значення позитивної величини (квадрата суми або різниці двох величин) не може бути негативним, тому

звідки

(3.29)

На рис. 3.4 наведено типові графіки кореляційної функції . Як видно з рис. 3.4, асимптотичне наближення функції до сталого значення може відбуватися як монотонно (рис. 3.4а), так і немонотонно (рис. 3.4б).

На практиці часто замість випадкового процесу розглядають його відхилення від математичного очікування , яке називається пульсаціями або флуктуаціями процесу.

Кореляційна функція пульсацій стаціонарного випадкового процесу дорівнює

.		(3.30)
Рис.3.4 Типові графіки кореляційної функції

З (3.30) видно, що математичне очікування пульсацій дорівнює нулю, а їх дисперсія визначається за формулою

.

(3.31)

Відношення

(3.32)

називають нормованою кореляційною функцією (коефіцієнтом кореляції) пульсацій випадкового процесу (або випадкового процесу з нульовим середнім). Типові графіки нормованої кореляційної функції пульсацій показано на рис. З.5.

Рис.3.5 Типові графіки нормованої кореляційної функції пульсацій

Для чисто випадкового стаціонарного процесу завжди можна визначити таке значення інтервалу , що при величини й можна вважати практично незалежними, причому практична незалежність розуміється в тому розумінні, що при абсолютна величина коефіцієнта кореляції залишається менше заданої величини :

.

(3.33)

Величина звичайно приймається рівною 0,05. Інтервал називають часом кореляції випадкового процесу. Час кореляції іноді визначається як половина ширини основи прямокутника одиничної висоти, площа якого дорівнює площі під графіком коефіцієнта кореляції (рис. 3.5, а), тобто

(3.34)

3.2.5 Ергодичність стаціонарних процесів. Існує клас випадкових процесів, які мають важливу для практичних задач властивість ергодичності.

Випадковий процес називають ергодичним, якщо усереднення по множині з імовірністю, якомога близькою до одиниці, дорівнює усередненню за часом.

Отже, для ергодичних процесів є чинними формули

;	(3.35)
;
;
.

Розгорнувши вирази середніх за множиною та часом, отримаємо

	(3.36)

Ергодична властивість випадкового процесу має істотне практичне значення. При дослідженні таких процесів немає необхідності вивчати велику сукупність реалізацій, а досить лише однієї реалізації, яка спостерігається протягом тривалого часу. Наприклад, статистичні властивості флуктуаційних шумів на виході електронних підсилювачів можна вивчати протягом досить тривалого часу на одному підсилювачі, а потім результати цього дослідження поширити на всі ідентичні пристрої.

3.2.6 Спектральна щільність стаціонарного випадкового процесу. Як відомо, при вивченні детермінованих сигналів досить зручним є гармонійний аналіз. У зв'язку із цим бажано було б використовувати апарат перетворень Фур'є і для випадкових процесів. Однак безпосереднє використання класичного гармонійного аналізу до випадкових процесів неможливо по наступних причинах:

1) реалізації випадкового процесу не задовольняють умові абсолютної інтегрованості

;

2) для випадкового процесу частотний спектр (у класичному представленні) також є випадковою функцією.

Рис.3.6 Реалізація випадкового процесу

Можна узагальнити гармонійний аналіз, здійснивши усереднення спектральних розкладань, які отримано для окремих реалізацій.

Для цього введемо нову функцію , що збігається на інтервалі з реалізацією випадкового процесу, а за межами цього інтервалу дорівнює нулю (рис. 3.6)

(3.37)

Для такої функції є чинним перетворення Фур'є

(3.38)

Середня потужність сигналу дорівнює

(3.39)

З іншого боку, середня потужність сигналу може бути визначена через частотний спектр

.

(3.40)

Функція , що є частиною (3.40), характеризує розподіл потужності реалізації по спектру частот і називається спектральною щільністю потужності.

Для визначення спектральної щільності сукупності реалізацій необхідно здійснити усереднення по ансамблю можливих значень функції :

.

Очевидно, що

,

тому

.

При , остаточно отримуємо

.

(3.41)

Таким чином, спектральна щільність , що є усередненою характеристикою сукупності реалізацій випадкового процесу, відповідає прямому перетворенню Фур'є для кореляційної функції. Зворотне перетворення Фур'є має вигляд

.

(3.42)

Перетворення (3.41) і (3.42), що зв'язують функції й , мають назву перетворень Хінчина - Вінера.

Якщо замість кругової частоти ввести частоту в герцах, то формули (3.41) і (3.42) приймуть вигляд

;	(3.43)
.	(3.44)

Для стаціонарних процесів усереднення по множині може бути замінено усередненням за часом, тому функція може бути представлена у вигляді

(3.45)

Таким чином, енергетичний спектр стаціонарного випадкового процесу може бути визначено двома шляхами:

а) безпосереднім спостереженням однієї реалізації та знаходженням межі (3.45);

б) знаходженням перетворення Фур'є кореляційної функції.

Функція відіграє велику роль при дослідженні перетворень випадкових сигналів у лінійних системах.

Для з'ясування фізичного смислу функції приймемо в (3.42)

.

(3.46)

Відомо, що виражає потужність сигналу, тому дає усереднену енергетичну картину розподілу потужності сигналу вздовж частотного спектру.

Із властивості перетворень Фур'є слідує, що при розширенні функції її частотний спектр стискується й, навпаки, при звуженні частотний спектр розширюється (рис. 3.7).

Рис.3.7 Перетворення Хінчина - Вінера

У зв'язку із цією властивістю розглянемо граничний випадок , коли спектральна щільність потужності є рівномірною на всіх частотах.

Випадковий процес, що має рівномірний на всіх частотах спектр, називають «білим шумом».

Функцію спектральної щільності білого шуму представлено на рис. 3.8, а.

Рис.3.8 Спектральна щільність та кореляційна функція білого шуму

Кореляційна функція білого шуму

(3.47)

оскільки інтеграл

є, як відомо, зворотним перетворенням Фур'є від дельта-функції .

Таким чином, кореляційна функція білого шуму відображується дельта ‑ функцією (рис. 3.8, б)

Білий шум характеризується тим, що його значення у будь-які два (навіть як завгодно близькі) моменти часу є некорельованими.

Необхідно підкреслити, що поняття «білий шум» засновано на спектральній властивості випадкового процесу й зовсім не пов'язане із законами розподілу щільності ймовірності. Зокрема, якщо білий шум має нормальний закон розподілу, то його називають нормальним білим шумом.

Білий шум є ідеалізацією, яка ніколи не зустрічається в реальних умовах, хоча б тому, що досить близькі значення випадкової функції практично завжди залежні, а також і тому, що реальні процеси мають кінцеву потужність, а для білого шуму повна потужність процесу нескінченна. Однак подібна ідеалізація в багатьох важливих практичних випадках значно спрощує математичний аналіз і не додає істотних погрішностей.

Спектри реальних процесів практично обмежені смугою частот внаслідок обмеженості смуги пропущення реальних систем.

Якщо білий шум пропустити через ідеальний фільтр низьких частот із граничними частотами , , то на виході отримаємо шум з обмеженим спектром (рис. 3.9).

Рис.3.9 Спектральна щільність	Рис.3.10 Кореляційна функція

Кореляційна функція такого сигналу

,

(3.48)

де - середня потужність процесу.

Графік кореляційної функції (3.48) представлено на рис. 3.10.

Для такого процесу інтервал кореляції має обмежену величину, яку можна визначити, наприклад, як інтервал між точкою й точкою, де перший раз обертається в нуль, тобто .

Отже, обмеження спектру спричиняє появі кореляції, причому зі скороченням смуги частот інтервал кореляції збільшується.

Якщо для випадкового процесу спектр неперервний і зосереджений біля деякої фіксованої частоти , причому виконується умова

,

(3.49)

то такий процес називається вузькосмуговим.

Якщо вузькосмуговий спектр має максимум при та є симетричним щодо цієї точки (рис. 3.11), то кореляційна функція процесу

.

Рис.3.11 Спектральна щільність вузькосмугового процесу

Оскільки за умовою смуга спектра є малою в порівнянні із частотою , то верхні межі інтегрування без особливої погрішності можна поширити нескінченно.

Беручи до уваги, що інтеграл від синуса в нескінченних межах дорівнює нулю, отримаємо

,

(3.50)

де

;

.

З (3.50) видно, що кореляційна функція вузькосмугового процесу, спектр якого розташовано симетрично біля деякої частоти , дорівнює помноженої на кореляційній функції , що відповідає спектру , якій отримано з вихідного зсувом на величину в напрямку низьких частот.

3.2.7 Ефективна ширина спектра випадкового процесу. При аналізі випадкових процесів із нерівномірним спектром (рис. 3.12) часто користуються поняттям еквівалентної або ефективної ширини спектра, яка визначається формулою

.

(3.51)

де - найбільше значення функції спектральної щільності.

Рис.3.12 Спектральна щільність процесу з нерівномірним спектром

Середня потужність процесу при цьому буде дорівнює

.

(3.52)

Інтервал кореляції визначається з урахуванням (3.41) співвідношенням

,

тому може бути встановлено наступний зв'язок між інтервалом кореляції й ефективною шириною спектра процесу:

.

(3.53)

Приклад 3.1. Знайти математичне очікування числа появ події в одному випробуванні, якщо ймовірність події дорівнює .

Випадкова величина - число появ подій в одному випробуванні - може приймати тільки два значення: (подія відбулася) з імовірністю й (подія не відбулася) з імовірністю . Шукане математичне очікування дорівнює

Отже, математичне очікування числа появ події в одному випробуванні дорівнює ймовірності цієї події.

Приклад. 3.2. Здійснено три постріли з ймовірностями влучення в ціль, рівними ; і . Знайти математичне очікування загального числа влучень.

Число влучень при першому пострілі є випадкова величина яка може приймати тільки два значення: 1 (влучення) з імовірністю й 0 (промах) з імовірністю .

Математичне очікування числа влучень при першому пострілі дорівнює ймовірності влучення (див. приклад 3.1), тобто . Аналогічно знайдемо математичні очікування числа влучень при другому й третьому пострілах

;

Загальне число влучень є також випадковою величиною, що складається із суми влучень у кожному із трьох пострілів:

.

Шукане математичне очікування дорівнює

.

Приклад 3.3. Знайти дисперсію випадкової величини , що задана наступним законом розподілу:

	1	2	5
	0,3	0,5	0,2

Дисперсія дискретної випадкової величини

Математичне очікування

.

Тоді шукана дисперсія

.

Приклад 3.4. Проводиться 10 незалежних випробувань, у кожному з яких імовірність появи події дорівнює . Знайти дисперсію числа появ події при випробуваннях.

Число появ події в незалежних випробуваннях складається з появ події в окремих випробуваннях, тобто .

Величини взаємно незалежні, тому дисперсія суми випадкових величин дорівнює сумі дисперсій цих величин.

На підставі (3.10) можна написати наступну формулу для дисперсії величини :

.

Математичне очікування числа появ події в одному випробуванні дорівнює ймовірності події (див. приклад 3.1), тому

.

Величина є математичним очікуванням випадкової величини .

Величина може приймати тільки два значення, а саме з імовірністю й з імовірністю , тому

.

Тоді

.

Очевидно, для випадкових величин за аналогією будемо мати

; ; …...; .

Отже, шукана дисперсія

.

Приклад 3.5. У вимірювальному приладі відстань між сусідніми значеннями шкали постійна й дорівнює а. При огрубленні відліку до найближчого цілого ділення погрішність округлення по абсолютній величині не перевищує половини відстані між сусідніми значеннями шкали.

Знайти щільність розподілу ймовірності, математичне очікування й дисперсію погрішності огрублення.

Погрішність при огрубленні відліку можна розглядати як випадкову величину , що може приймати з рівною ймовірністю будь-які значення в межах від до . Отже, щільність розподілу випадкової величини постійна в межах від до й дорівнює нулю за цими межами.

Відомо, що

,

тому

.

Аналітично закон рівномірного розподілу можна записати наступним чином:

Математичне очікування й дисперсія погрішності округлення дорівнюють:

.

.

Приклад 3.6 Випадкова величина розподілена за нормальним законом, який задається функцією

.

Показати, що є математичне очікування, а — дисперсія випадкової величини .

Відповідно до (3.7) математичне очікування випадкової величини

.

Уведемо нову змінну

.

Звідси

.

Тоді отримаємо

.

Перший доданок правої частини дорівнює нулю, тому що під знаком інтеграла непарна функція. Відомо, що інтеграл

,

тоді

.

Дисперсія відповідно до (3.8)

.

Уведемо нову змінну

.

Звідси

.

Тоді

.

Інтегруючи вроздріб, поклавши й , після певних перетворень отримаємо

.

Приклад 3.7. Контрольно-вимірювальний пристрій має систематичну погрішність +30 мВ і випадкову погрішність, розподілену за нормальним законом зі середньоквадратичним відхиленням 10 мВ. Знайти ймовірність того, що загальна погрішність пристрою прийме значення, що належить інтервалу 10 ‑ 50 мВ.

Імовірність того, що погрішність пристрою не перевищить по абсолютній величині заданої межі, дорівнює

.

Введемо нову змінну

.

Звідси

.

Тоді

.

Користуючись функцією Лапласа

остаточно отримаємо

.

У нашому випадку

мВ і мВ.

Тоді за допомогою таблиці функції Лапласа (додаток 1) знаходимо

.

Приклад 3.8. Знайти спектральну щільність для процесу з кореляційною функцією виду функції.

Виходячи з визначення функції як межі прямокутного імпульсу , тривалості й висоти при інтеграл , де - довільна функція, може бути представлено у вигляді

.

Відповідно до теореми про середнє значення маємо:

.

Таким чином,

.

(3.54)

Тоді, відповідно до загальної формули (3.41), згідно з (3.54) знайдемо спектральну щільність

.

Отже, при кореляційній функції типу функції спектр рівномірний на всіх частотах (сигнал типу «білий шум», див. рис. 3.8 а та б).

Приклад 3.9. Знайти кореляційну функцію періодичного сигналу з періодом .

Кореляційна функція сигналу дорівнює

.

Представимо періодичну функцію рядом Фур'є

.

Тоді

.

Відомо, що , тому дріб дорівнює нулю за будь-яких комбінацій і крім . Отже,

.

Як видно з отриманої формули, кореляційна функція періодичного сигналу з періодом є періодичною функцією аргументу з тим же періодом . Амплітуда гармоніки кореляційної функції дорівнює подвоєному квадрату амплітуди відповідної гармоніки . При цьому як парна функція розкладається в ряд по косинусах.

Приклад 3.10. Нормована спектральна щільність випадкової функції постійна на деякому інтервалі частот , і дорівнює нулю поза цим інтервалом (рис. 3.13). Визначити нормовану кореляційну функцію.

Рис.3.13 Нормована спектральна щільність

Виходячи з умови, що площа, обмежена кривою , дорівнює одиниці, знаходимо значення при .

;

.

З (3.42) маємо

.
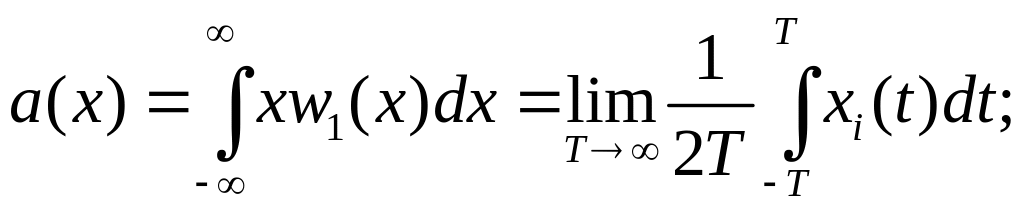
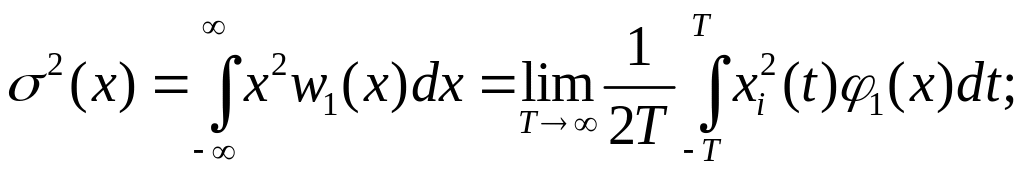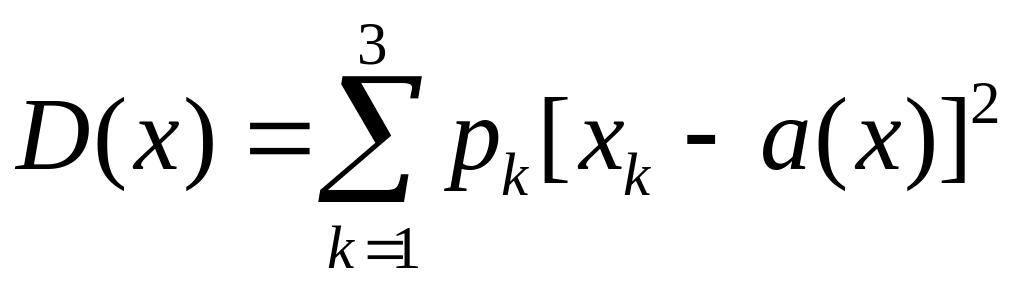
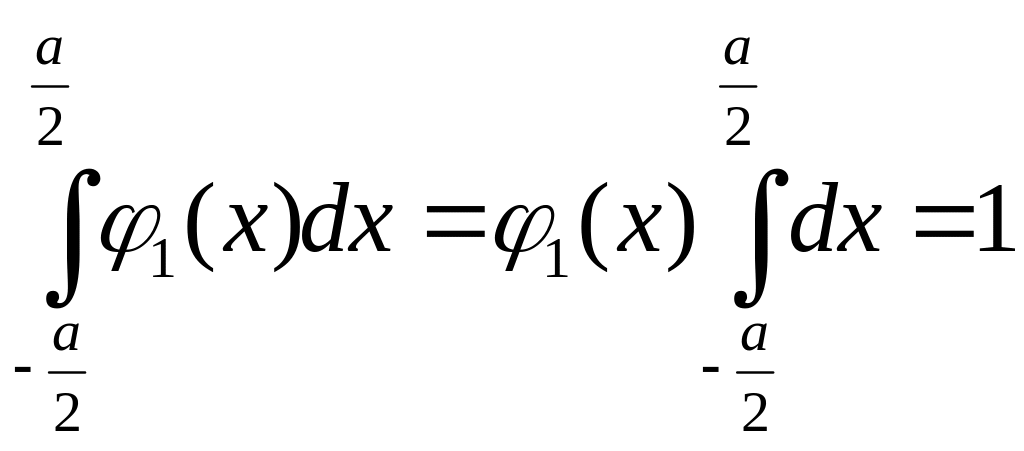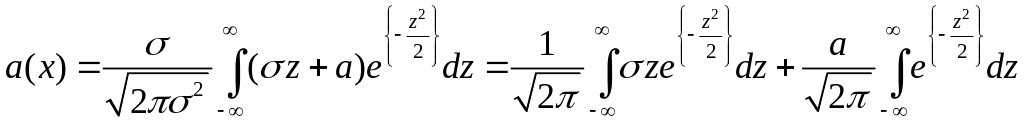
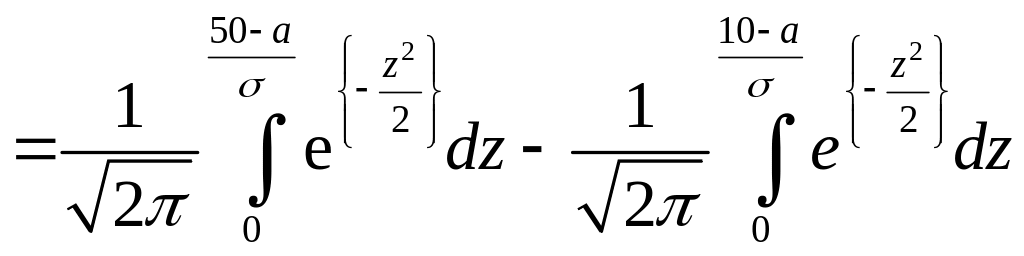