
- •Міністерство освіти і науки україни
- •Методичні вказівки
- •Практичне заняття №1 спектри періодичних сигналів
- •1.1 Мета заняття
- •1.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •1.3 Задачі для самостійної роботи
- •1.4 Контрольні запитання і завдання
- •Практичне заняття №2 спектри неперіодичних сигналів
- •2.1 Мета заняття
- •2.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •2.3 Задачі для самостійної роботи
- •2.4 Контрольні запитання і завдання
- •3.1 Мета заняття
- •3.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,8].
- •3.3 Задачі для самостійної роботи
- •3.4 Контрольні запитання і завдання
- •Практичне заняття №4 ентропія та її властивості
- •4.1 Мета заняття
- •4.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,7,9].
- •4.3 Задачі для самостійної роботи
- •4.4 Контрольні запитання і завдання
- •Практичне заняття №5 ентропія неперервних джерел інформації
- •5.1 Мета заняття
- •5.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •5.3 Задачі для самостійної роботи
- •5.4 Контрольні запитання і завдання
- •Практичне заняття №6 ефективне кодування
- •6.1 Мета заняття
- •6.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •6.3 Задачі для самостійної роботи
- •6.4 Контрольні запитання і завдання
- •Практичне заняття №7
- •7.1 Мета заняття
- •7.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •7.3 Задачі для самостійної роботи
- •7.4 Контрольні запитання і завдання
- •Практичне заняття №8 циклічні коди
- •8.1 Мета заняття
- •8.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •8.3 Задачі для самостійної роботи
- •8.4 Контрольні запитання і завдання
- •Навчальне видання методичні вказівки
- •Хнуре. Україна. 61166, Харків, просп. Леніна, 14 Віддруковано в навчально-науковому
- •61166, Харків, просп. Леніна, 14
7.4 Контрольні запитання і завдання
1 Як обчислюється швидкість передачі інформації через дискретний канал з перешкодами?
2 Як визначається пропускна здатність дискретного каналу з перешкодами?
3 У чому полягає сутність теореми Шеннона для дискретного каналу з перешкодами?
4 Поясніть характер залежності пропускної здатності неперервного каналу з перешкодами від смуги пропущення каналу.
5 Які коди називають коригувальними?
6 Як визначається відстань між кодовими комбінаціями?
7 Що розуміється під кодовою відстанню?
8 Висвітлити методику побудови коду Хемінга?
9 У чому полягає логіка декодування Хемінга?
Практичне заняття №8 циклічні коди
8.1 Мета заняття
Метою заняття є ознайомлення студентів з методами циклічного кодування, що застосовуються у системах передачі дискретної інформації за умов наявності перешкод.
8.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
Циклічні коди є різновидом систематичних кодів і тому мають усі їх властивості. Спочатку вони були створені для спрощення схем кодування й декодування. Їх ефективність при виявленні та виправленні помилок забезпечила їм широке застосування на практиці.
Циклічні коди більш зручно розглядати, представляючи комбінацію двійкового коду не у вигляді послідовностей нулів і одиниць, а у вигляді полінома деякого ступеня:
|
(8.1) |
де
-
основа системи числення;
![]() - цифри даної системи числення (у двійковій
системі 0 і 1).
- цифри даної системи числення (у двійковій
системі 0 і 1).
Наприклад, двійкова послідовність 01001 може бути записана у вигляді полінома від змінної x:
|
(8.2) |
Представлення
кодових комбінацій у формі (8.2) дозволяє
звести дії над комбінаціями до дій над
поліномами. При цьому додавання двійкових
поліномів зводиться до додавання по
модулю два коефіцієнтів при рівних
ступенях змінної
.
Множення виконується за звичайним
правилом множення ступеневих функцій,
однак отримані в цьому випадку коефіцієнти
при відповідних ступенях складаються
за модулем два. Ділення здійснюється
за правилами ділення ступеневих функцій.
Основна властивість циклічних кодів,
яка визначає їх назву, полягає в
наступному. Якщо комбінація
![]() є дозволеною, то комбінація, одержана
з неї шляхом циклічної перестановки
розрядів, тобто комбінація
є дозволеною, то комбінація, одержана
з неї шляхом циклічної перестановки
розрядів, тобто комбінація
![]() ,
також належить цьому коду.
,
також належить цьому коду.
Представлення комбінацій у
формі (8.1), (8.2) зручно ще й тим, що згадана
циклічна перестановка є результатом
простого множення даного полінома на
.
Дійсно, якщо одна з кодових комбінацій
відображується поліномом
![]() ,
то нова комбінація за рахунок циклічного
зсуву буде мати вигляд
,
то нова комбінація за рахунок циклічного
зсуву буде мати вигляд
![]() .
Однак в останньому члені необхідно
замінити
.
Однак в останньому члені необхідно
замінити
![]() на 1 (інакше довжина кодової комбінації
перевищить значення
).
Отже, отримана комбінація
на 1 (інакше довжина кодової комбінації
перевищить значення
).
Отже, отримана комбінація
![]() є циклічним зсувом комбінації
є циклічним зсувом комбінації
![]() .
.
Ідея
побудови циклічних кодів базується на
використанні поліномів, що не приводяться.
Поліном називається таким, що не
приводиться, якщо не може бути представленим
у вигляді добутку поліномів нижчих
ступенів, тобто такий поліном ділиться
тільки на себе або на одиницю й не
ділиться ні на який інший поліном. На
такий поліном ділиться без залишку
довільний поліном
![]() .
.
Поліноми,
що не приводяться, у теорії циклічних
кодів відіграють роль утворюючих
поліномів. У табл. 8.1 наведено всі
поліноми, які не приводяться, до 5-го
ступеня включно, які позначено
![]() , де
- порядковий номер полінома, що не
приводиться, ступеня
при розташуванні по ознаці зростання
відповідних їм двійкових чисел.
, де
- порядковий номер полінома, що не
приводиться, ступеня
при розташуванні по ознаці зростання
відповідних їм двійкових чисел.
Таблиця
8.1 Таблиця поліномів, що не приводяться
![]()
№ |
Кодове позначення |
|
Умовна позначка |
|
|||
1 |
11 |
|
|
|
|||
2 |
111 |
|
|
|
|||
3 |
1011 |
|
|
4 |
1101 |
|
|
|
|||
5 |
10011 |
|
|
6 |
11001 |
|
|
7 |
11111 |
|
|
|
|||
8 |
100101 |
|
|
9 |
101001 |
|
|
10 |
101111 |
|
|
11 |
110111 |
|
|
12 |
111011 |
|
|
13 |
111101 |
|
|
Щоб
зрозуміти принцип побудови циклічного
коду, помножимо комбінацію простого
k-значного
коду
![]() на одночлен
на одночлен
![]() ,
а
потім розділимо на утворюючий поліном
,
а
потім розділимо на утворюючий поліном
![]() ,
ступінь якого дорівнює
.
Після множення
на
ступінь кожного одночлена, що входить
в
,
підвищується на
.
При діленні добутку
,
ступінь якого дорівнює
.
Після множення
на
ступінь кожного одночлена, що входить
в
,
підвищується на
.
При діленні добутку
![]() на утворюючий поліном утворюється ціла
частина
на утворюючий поліном утворюється ціла
частина
![]() такого ж ступеня, як і
.
Результат множення й ділення можна
представити як
такого ж ступеня, як і
.
Результат множення й ділення можна
представити як
|
(8.3) |
де
![]() - залишок від ділення
- залишок від ділення
![]() на
.
на
.
Ціла
частина
має такий же ступінь, як і кодова
комбінація
простого коду, тому
є кодовою комбінацією цього ж простого
k‑
значного
коду. Слід відзначити, що ступінь залишку
не може перевищувати ступінь утворюючого
полінома, тобто його найвищий ступінь
може бути
![]() .
Отже, найбільше число розрядів залишку
не перевищує числа
.
.
Отже, найбільше число розрядів залишку
не перевищує числа
.
Помноживши обидві частини рівності (8.3) на , отримуємо
|
(8.4) |
В
(8.4) знак мінус перед
![]() замінено знаком плюс, тому що вирахування
по модулю два зводиться до додавання.
замінено знаком плюс, тому що вирахування
по модулю два зводиться до додавання.
Таким чином, кодова комбінація циклічного n-значного коду може бути отримана двома способами:
множенням кодової комбінації простого коду на одночлен і додаванням до цього добутку залишку , який отримано в результаті ділення добутку на утворюючий поліном ;
множенням кодової комбінації простого k-значного коду на утворюючий поліном .
При
побудові циклічних кодів першим способом
розташування інформаційних символів
в усіх комбінаціях є строго впорядкованим
- вони займають k
старших розрядів комбінації, а інші (![]() )
розрядів використовуються як перевірочні
(контрольні).
)
розрядів використовуються як перевірочні
(контрольні).
При другому способі утворення циклічних кодів інформаційні й контрольні символи в комбінаціях циклічного коду не відділені друг від друга, що ускладнює процес декодування. Тому в основному застосовують перший спосіб побудови циклічного коду.
Важливою задачею побудови
циклічних кодів є вибір утворюючого
полінома, який задовольняє заздалегідь
заданим умовам. Якщо код призначено для
виправлення незалежних помилок, такою
умовою є забезпечення заданої кодової
відстані
.
У випадку, коли код призначено для
виправлення пакетів помилок, умовою є
довжина пакета
![]() помилок, який треба
виправити або виявити.
помилок, який треба
виправити або виявити.
Порядок знаходження поліному
починається з вибору інформаційних
розрядів
за заданим об'ємом коду
![]() .
Потім визначається найменша довжина
кодового слова
,
яка забезпечує виявлення або виправлення
помилок заданої кратності. Для циклічних
кодів ця проблема зводиться до знаходження
потрібного полінома
.
.
Потім визначається найменша довжина
кодового слова
,
яка забезпечує виявлення або виправлення
помилок заданої кратності. Для циклічних
кодів ця проблема зводиться до знаходження
потрібного полінома
.
Утворюючий поліном потрібно вибирати, як це було відзначено вище, з урахуванням того, що його ступінь повинна бути рівною числу перевірочних символів . Крім цього, поліном повинен входити як співмножник у розкладання двочлена
|
(8.5) |
Доведено, що будь-який двочлен типу (8.5) може бути представлено добутком усіх без винятку поліномів, що не приводяться, ступені яких являються дільниками числа (від 1 до включно). Отже, для кожного існує, принаймні, один поліном, що не приводиться, ступеня , який входить співмножником у розкладання двочлена .
Боуз і Чоудхурі показали, що для будь-яких
цілих позитивних чисел
,
![]() існує циклічний код значності
існує циклічний код значності
|
(8.6) |
з кодовою відстанню
|
(8.7) |
При цьому число перевірочних
символів
![]() не перевищує величини
не перевищує величини
![]() ,
тобто
,
тобто
|
(8.8) |
Такий код гарантовано виправляє
помилки кратності
та менше або виявляє помилки кратності
![]() й менше. Крім того, код виявляє всі пакети
помилок, довжина яких дорівнює або менше
.
й менше. Крім того, код виявляє всі пакети
помилок, довжина яких дорівнює або менше
.
Співвідношення (8.6) - (8.8) можуть бути використані для вибору утворюючого полінома.
Слід зазначити, що якщо є помилки різної кратності, то в першу чергу необхідно усунути однократні помилки, імовірність появи яких найбільша.
Оскільки в циклічному коді
опізнавачем помилок є залишки від
ділення поліномів помилок на утворюючий
поліном
,
то
повинен забезпечувати необхідне число
різних залишків при діленні векторів
помилок з одиницею в помилковому розряді
(тому що вектор одиночної помилки має
одиницю тільки в помилковому розряді
й нулі в усіх інших розрядах). Як утворюючі
поліноми використовують поліноми, що
не приводяться, які дають найбільше
число залишків. При ступені поліному
![]() він може дати
він може дати
![]() ненульових залишків (нульовий залишок
є опізнавачем безпомилкової передачі).
ненульових залишків (нульовий залишок
є опізнавачем безпомилкової передачі).
Отже, необхідною умовою виправлення будь-якої одиночної помилки є виконання нерівності
|
|
Здатність циклічного коду
виявляти помилки обумовлюється не
тільки ступенем утворюючого полінома,
але й числом його членів. Чим більше
залишків може бути утворено при діленні
поліному повідомлення на утворюючий
поліном, тим вище коригувальна здатність
коду. Найбільше число залишків, рівне
![]() (крім нульового), може забезпечити тільки
поліном ступеня
,
який не приводиться.
(крім нульового), може забезпечити тільки
поліном ступеня
,
який не приводиться.
Для побудови циклічного
![]() - коду, який забезпечує виявлення або
виправлення помилок заданої кратності,
як вже відзначалося, насамперед, варто
вибрати утворюючий поліном ступеня
- коду, який забезпечує виявлення або
виправлення помилок заданої кратності,
як вже відзначалося, насамперед, варто
вибрати утворюючий поліном ступеня
![]() .
Він повинен входити як співмножник у
розкладання двочлена
.
Він повинен входити як співмножник у
розкладання двочлена
![]() .
Однак не всякий поліном ступеня
,
що входить у розкладання даного двочлена,
може бути використано для утворення
потрібного
- коду. При побудові додаткової матриці
.
Однак не всякий поліном ступеня
,
що входить у розкладання даного двочлена,
може бути використано для утворення
потрібного
- коду. При побудові додаткової матриці
![]() по обраному поліному необхідно також
ураховувати кількість рядків у циклі
чергування перевірочних розрядів і
вагу
по обраному поліному необхідно також
ураховувати кількість рядків у циклі
чергування перевірочних розрядів і
вагу
![]() кожного рядка (кількість одиниць). У
прикладі 8.5 це питання розглянуте більш
докладно.
кожного рядка (кількість одиниць). У
прикладі 8.5 це питання розглянуте більш
докладно.
У загальному випадку при
побудові циклічного
- коду з виправленням у кодових комбінаціях
помилок як утворюючий поліном ступеня
вибирається добуток зі
співмножників старших ступенів, що
входять у розкладання двочлена виду
![]() .
.
При виборі утворюючого полінома необхідно відзначити дуже коштовну властивість циклічних кодів. Для цього введемо поняття зворотного полінома.
Зворотними поліномами
називаються такі поліноми, які утворяться
шляхом підстановки
![]() замість
в основний поліном і множення цього
полінома на одночлен
замість
в основний поліном і множення цього
полінома на одночлен
![]() ,
де
- ступінь основного полінома. Наприклад,
основний поліном ступеня m
= 5
,
де
- ступінь основного полінома. Наприклад,
основний поліном ступеня m
= 5
|
|
Зворотний йому поліном
|
|
Виконавши операцію множення й розташувавши члени по убуванню ступенів, отримаємо
|
|
Порівнюючи вирази основного й зворотного поліномів, які записано у двійковій формі, бачимо, що нулі й одиниці у зворотному поліномі розташовано у зворотному порядку в порівнянні з основним поліномом.
Слід зазначити, що добуток
деякого полінома
на основний
![]() є взаємозворотним добутку цього ж
полінома на взаємо-зворотний поліном
є взаємозворотним добутку цього ж
полінома на взаємо-зворотний поліном
![]() :
:
![]() ,
зворотний
,
зворотний
![]() .
.
Поняття про зворотні поліноми
є корисним для вибору утворюючих
поліномів при побудові циклічних кодів.
Наприклад, якщо буде встановлено, що
поліном
придатний для побудови циклічного коду
із заданими характеристиками, то й
зворотний йому поліном
буде також придатний для побудови
циклічного коду з тими ж характеристиками.
Ці коди відрізняються тільки порядком
розташування залишків. Наприклад,
матриці залишків для основного полінома
![]() й зворотного йому полінома
й зворотного йому полінома
![]() мають вигляд
мають вигляд
|
|
Порівнюючи ці матриці, можна помітити, що рядки у другої матриці розташовано у зворотному порядку, причому розряди в цих рядках також розташовані у зворотному порядку.
Табличні й розрахункові
методи знаходження утворюючих поліномів
циклічних кодів далеко не завжди
дозволяють однозначно вибирати найкращий
поліном для певного типу каналу й певного
характеру розподілу помилок. Тому широке
розповсюдження отримали машинні методи
відбору найкращих кодів та їх утворюючих
поліномів. Так, за допомогою обчислювальної
машини зроблено відбір утворюючих
поліномів циклічних кодів, які найбільше
підходять для виявлення помилок у
телефонних каналах. Зазначений відбір
зроблено на підставі статистичних даних
розподілу помилок при передачі сигналів
методом відносної фазової модуляції
(ВФМ) зі швидкістю 1200 бод. Імовірність
помилки (по імпульсах) при цьому становила
![]() -
-
![]() .
.
Важливою властивістю циклічних кодів є те, що всі вони будуються за допомогою утворюючого полінома . Розглянемо методику побудови циклічного коду. Утворюючий поліном використовують в утворенні кожної кодової комбінації, тому комбінація коду ділиться на утворюючий поліном без залишку. Однак без залишку діляться тільки ті поліноми (комбінації), які належать даному коду, тобто утворюючий поліном дозволяє вибрати дозволені кодові комбінації із всіх можливих. Якщо ж при діленні прийнятої кодової комбінації циклічного коду на утворюючий поліном буде отримано залишок, то має місце помилка. Таким чином, залишки від ділення прийнятої комбінації на утворюючий поліном є опізнавачами помилок циклічних кодів. Але дані залишки ще не вказують безпосередньо на місце помилки у кодовій комбінації.
У циклічних кодах ідея виправлення помилок ґрунтується на наступному. Помилкова комбінація після певного числа циклічних зсувів «підганяється» під залишок таким чином, щоб у сумі з залишком вона давала б виправлену комбінацію. Залишок при цьому являє собою різницю між помилковим й правильними символами, а одиниці в залишку стоять на місцях помилкових розрядів в «підігнаній» циклічними зсувами комбінації. «Підганяють» спотворену комбінацію доти, поки число одиниць в залишку не буде рівним числу помилок у коді. При цьому, природно, число одиниць може дорівнювати числу помилок , які виправляються даним кодом (код виправляє три помилки й у спотвореній комбінації три помилки) або менше (код виправляє три помилки, у прийнятій комбінації - одна помилка).
Таким чином, для виявлення й виправлення помилкового розряду здійснюють наступні операції:
прийняту комбінацію ділять на утворюючий поліном;
визначають кількість одиниць в залишку (вага залишку ). Якщо
 ,
де
- припустиме число помилок, які
виправляються даним кодом, прийняту
комбінацію складають по модулю два з
отриманим залишком. Сума дає виправлену
комбінацію. Якщо
,
де
- припустиме число помилок, які
виправляються даним кодом, прийняту
комбінацію складають по модулю два з
отриманим залишком. Сума дає виправлену
комбінацію. Якщо
 ,
то
,
топроводять циклічний зсув прийнятої комбінації вліво на один розряд. Комбінацію, отриману в результаті циклічного зсуву, ділять на утворюючий поліном . Якщо в результаті повторного ділення , то ділене підсумують із залишком;
проводять циклічний зсув вправо на один розряд комбінації, отриманої в результаті визначення суми останнього діленого з останнім залишком. Отримана комбінація вже не містить помилок. Якщо після першого циклічного зсуву й наступного ділення залишок виходить таким, що його вага , то
повторюють операцію п. 3 доти, поки не буде досягнуто . У цьому випадку комбінацію, отриману в результаті останнього циклічного зсуву, підсумують із залишком від ділення цієї комбінації на утворюючий поліном;
проводять циклічний зсув вправо рівно на стільки розрядів, на скільки зрушено останню комбінацію щодо прийнятої комбінації. У результаті отримаємо виправлену комбінацію.
Приклад
8.1. Дано
![]() і утворюючий поліном третього ступеня
і утворюючий поліном третього ступеня
![]() .
Отже, кодові комбінації циклічного коду
будуть мати по сім розрядів. Потрібно
записати довільну кодову комбінацію
циклічного коду (7,4) способом множення
кодової комбінації
простого коду на одночлен
і додавання до нього залишку, отриманого
в результаті ділення добутку
на утворюючий поліном. Візьмемо довільну
чотирьохрозрядну комбінацію 0111, тобто
.
Отже, кодові комбінації циклічного коду
будуть мати по сім розрядів. Потрібно
записати довільну кодову комбінацію
циклічного коду (7,4) способом множення
кодової комбінації
простого коду на одночлен
і додавання до нього залишку, отриманого
в результаті ділення добутку
на утворюючий поліном. Візьмемо довільну
чотирьохрозрядну комбінацію 0111, тобто
![]() .
Знайдемо добуток
.
Знайдемо добуток
![]() .
Розділимо результат на поліном
.
Розділимо результат на поліном
![]() :
:
|
|
Отже,
залишок
![]() .
.
Таким
чином, у відповідності зі сформульованим
раніше правилом знайдемо комбінацію,
яка належить циклічному коду (7,4):
![]() або у двійковій формі
або у двійковій формі
![]() .
.
Операція утворення циклічного коду може безпосередньо проводитися при запису вихідних кодових комбінацій у вигляді двійкових чисел.
Приклад
8.2. Дано
та утворюючий поліном
![]() .
Отже, кодові комбінації циклічного коду
будуть мати сім розрядів
.
Отже, кодові комбінації циклічного коду
будуть мати сім розрядів
![]() .
Візьмемо довільне чотирьохрозрядне
двійкове число
.
Візьмемо довільне чотирьохрозрядне
двійкове число
![]() .
Знайдемо добуток
.
Знайдемо добуток
![]() .
Розділимо результат на
.
Розділимо результат на
![]() :
:
|
|
У
результаті ділення вийде залишок
![]() .
Отже, комбінація циклічного коду (7,4)
запишеться в такий спосіб:
.
Отже, комбінація циклічного коду (7,4)
запишеться в такий спосіб:
|
|
Приклад
8.3. Дано
![]() - утворюючий поліном. Побудувати циклічний
код із простого чотиризначного коду
способом множення кодової комбінації
простого k-значного
коду на утворюючий поліном
.
У якості вихідної використаємо просту
комбінацію
- утворюючий поліном. Побудувати циклічний
код із простого чотиризначного коду
способом множення кодової комбінації
простого k-значного
коду на утворюючий поліном
.
У якості вихідної використаємо просту
комбінацію
![]() .
Операція множення цієї комбінації на
утворюючий поліном
запишеться в такий спосіб:
.
Операція множення цієї комбінації на
утворюючий поліном
запишеться в такий спосіб:
|
|
Отже, просту чотирьохсимвольну комбінацію можна відобразити за допомогою сьомисимвольного циклічного коду
|
|
Результати розрахунків для всієї множини кодових комбінацій цього коду наведено в таблиці нижче
Таблиця 8.2 Результати циклічного кодування
Простий чотирьохсимвольний код |
Утворюючий поліном |
Циклічний (7,4)-код
|
|
1101 |
|
Приклад 8.4.
Дана кількість інформаційних розрядів
,
яка задається виходячи з кількості
переданих повідомлень
.
Необхідно визначити утворюючий поліном
для циклічного коду, який забезпечує
усунення однократних помилок або
виявлення двократних (![]() ,
,![]() ). Зі співвідношення (8.7)
визначаємо мінімальну кодову відстань
). Зі співвідношення (8.7)
визначаємо мінімальну кодову відстань
![]() .
Кількість перевірочних розрядів
.
Кількість перевірочних розрядів
![]() .
.
Для побудови циклічного коду
необхідно вибрати утворюючий поліном
ступеня три. Користуючись табл. 8.1,
вибираємо один із двох наявних поліномів
третього ступеня, наприклад,
.
Тепер для побудови циклічного коду
залишається помножити кожну просту
чотирьохсимвольну комбінацію
ненадлишкового коду
на утворюючий поліном. Доведемо чинність
співвідношення (8.8). Для цього визначимо
значність коду
![]() .
Утворюючий поліном
повинен входити як співмножник у
розкладання двочлена
.
Тому що
,
то цей двочлен має вигляд
.
Утворюючий поліном
повинен входити як співмножник у
розкладання двочлена
.
Тому що
,
то цей двочлен має вигляд
![]() .
Його складові множники повинні бути
поліномами, що не приводяться, ступені
яких є дільниками числа
.
.
Його складові множники повинні бути
поліномами, що не приводяться, ступені
яких є дільниками числа
.
Зі співвідношення (8.6) визначаємо
![]() .
До чисел, на які
ділиться без залишку, належать одиниця
й три. Отже, співмножниками двочлена
повинні бути поліноми, що не приводяться,
першого та третього ступенів. Вибравши
з табл. 8.1 поліноми, що не приводяться,
зазначених ступенів, отримаємо повне
розкладання двочлена
.
До чисел, на які
ділиться без залишку, належать одиниця
й три. Отже, співмножниками двочлена
повинні бути поліноми, що не приводяться,
першого та третього ступенів. Вибравши
з табл. 8.1 поліноми, що не приводяться,
зазначених ступенів, отримаємо повне
розкладання двочлена
![]() .
Визначивши число
,
переконуємося у виконанні співвідношення
(
.
Визначивши число
,
переконуємося у виконанні співвідношення
(![]() ).
).
Приклад 8.5.
Побудувати циклічний
- код з виправленням у кодових комбінаціях
одиночних помилок
![]() .
.
Нехай загальне число елементів
кодової комбінації дорівнює 15. Число
перевірочних розрядів визначаємо зі
співвідношення (8.8). По формулі (8.6)
![]() .
Отже,
.
Число інформаційних елементів
.
Отже,
.
Число інформаційних елементів
![]() .
Для
,
маємо
.
Для
,
маємо
![]() .
Число перевірочних розрядів
ділиться без залишку на 1, 2 і 4, тому
співмножниками поліному
.
Число перевірочних розрядів
ділиться без залишку на 1, 2 і 4, тому
співмножниками поліному
![]() повинні бути всі поліноми, що не
приводяться, 1-го, 2-го і 4-го ступенів.
Користуючись таблицею поліномів,
отримаємо
повинні бути всі поліноми, що не
приводяться, 1-го, 2-го і 4-го ступенів.
Користуючись таблицею поліномів,
отримаємо
|
|
З усіх співмножників розкладання
двочлена
потрібно вибрати один зі співмножників
четвертого ступеня
![]() .
Щоб установити, який із трьох співмножників
четвертого ступеня може бути використано
як утворюючий поліном, знайдемо для
кожного з них додаткову матрицю
.
Щоб установити, який із трьох співмножників
четвертого ступеня може бути використано
як утворюючий поліном, знайдемо для
кожного з них додаткову матрицю
![]() .
.
Розділимо одиницю із приписаними праворуч нулями на поліноми
![]() ;
;
![]() ;
;
![]()
та отримаємо відповідні підматриці:


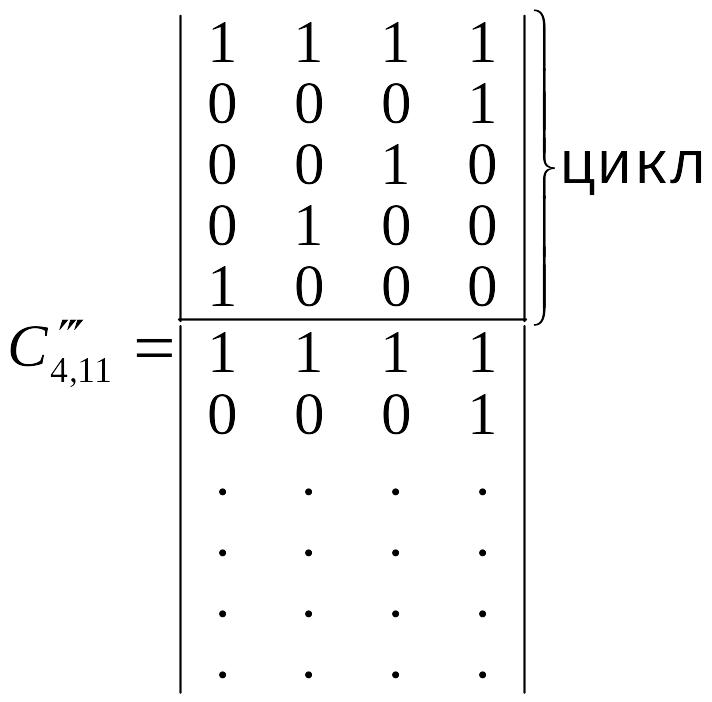 .
.
Для виправлення одиночних помилок додаткові матриці повинні вибиратися таким чином, щоб вага кожного рядка матриці мала не менше трьох одиниць (тобто кодової відстані).
Кожний рядок одиничної
транспонованої матриці
![]() має вагу, яка дорівнює одиниці, тому
вага будь-якого рядка додаткової матриці
повинна бути не менше двох одиниць. Ця
вимога буде виконана, якщо як утворюючий
поліном для побудови циклічного (15,11) -
коду вибрати один із двох співмножників:
має вагу, яка дорівнює одиниці, тому
вага будь-якого рядка додаткової матриці
повинна бути не менше двох одиниць. Ця
вимога буде виконана, якщо як утворюючий
поліном для побудови циклічного (15,11) -
коду вибрати один із двох співмножників:
![]() або
або
![]() .
Розглядаючи додаткову матрицю
.
Розглядаючи додаткову матрицю
![]() ,
можна помітити, що цикл чергування її
рядків (залишків) дорівнює п'яти, у той
час як для (15,11) - коду цей цикл повинен
дорівнювати числу інформаційних розрядів
,
можна помітити, що цикл чергування її
рядків (залишків) дорівнює п'яти, у той
час як для (15,11) - коду цей цикл повинен
дорівнювати числу інформаційних розрядів
![]() .
Крім того, з п'яти рядків матриці тільки
перший рядок має необхідну вагу (
.
Крім того, з п'яти рядків матриці тільки
перший рядок має необхідну вагу (![]() ), вага ж інших рядків є
недостатньою (
), вага ж інших рядків є
недостатньою (![]() ). Тому співмножник
не може бути використаний як утворюючий
поліном для побудови циклічного (15,11) -
коду. Вибравши як утворюючий поліном
один з поліномів
або
,
можна побудувати виробляючу матрицю
(15,11) - коду.
). Тому співмножник
не може бути використаний як утворюючий
поліном для побудови циклічного (15,11) -
коду. Вибравши як утворюючий поліном
один з поліномів
або
,
можна побудувати виробляючу матрицю
(15,11) - коду.
Матриці
![]() ,
,
![]() відрізняються одна від іншої тільки
порядком чергування рядків. Перестановка
рядків у додатковій матриці приводить
до
відрізняються одна від іншої тільки
порядком чергування рядків. Перестановка
рядків у додатковій матриці приводить
до
![]() еквівалентних циклічних (15,11) - кодів.
Практично при виборі з величезної
кількості кодів, еквівалентних за
коригувальною здатністю та надмірністю,
оптимального варіанта керуються
економічністю пристроїв для кодування
і декодування.
еквівалентних циклічних (15,11) - кодів.
Практично при виборі з величезної
кількості кодів, еквівалентних за
коригувальною здатністю та надмірністю,
оптимального варіанта керуються
економічністю пристроїв для кодування
і декодування.
Приклад 8.6.
Побудувати циклічний код (7, 4) для
числа
![]() .
.
Як утворюючий поліном візьмемо
![]() .
.
1. Помножимо
![]() на
на
![]() .
.
Маємо:
![]() .
.
2. Розділимо
![]() на утворюючий поліном
на утворюючий поліном


 або
або

Залишок
![]() має порядок
має порядок
![]() ,
тобто
,
тобто
![]() .
Остаточно циклічний код для 1010
буде
.
Остаточно циклічний код для 1010
буде ![]()
Якщо як утворюючий поліном
вибрати![]() ,
то будемо мати:
,
то будемо мати:
![]()


Остаточно: 1010011.
Приклад 8.7. Корекція помилки циклічного коду.
При передачі комбінації
1001110 циклічного коду, який виправляє
одиночні помилки (![]() ), отриманого за допомогою
утворюючого полінома
,
відбулася помилка в четвертому розряді.
Прийнята комбінація має вигляд 1000110.
Виконаємо корекцію помилки.
), отриманого за допомогою
утворюючого полінома
,
відбулася помилка в четвертому розряді.
Прийнята комбінація має вигляд 1000110.
Виконаємо корекцію помилки.
1) ділимо прийнятий код на .

2) Порівнюємо вагу отриманої
залишку
![]() .
.
3) Здійснюємо циклічний зсув прийнятої комбінації на 1 розряд та ділимо на :

4) Повторюємо пункт 3 доти, поки не буде
виконана умова:
![]()
а) |
б) |
в) |
|
|
|
|
|
|
5) Складаємо по модулю два останнє ділене з останнім залишком

6) Робимо циклічний зсув
комбінації, яку отримано в результаті
підсумовування останнього діленого з
останнім залишком, вправо на чотири
розряди (тому що перед цим ми чотири
рази зрушували прийняту комбінацію
вліво):
![]() .
Як бачимо, остання комбінація відповідає
переданій, тобто не містить помилки.
.
Як бачимо, остання комбінація відповідає
переданій, тобто не містить помилки.

 ,
, ,
,
 .
. .
. .
.




