5.3 Задачі для самостійної роботи

5.3.1 Визначити диференціальну ентропію рівномірного на інтервалі розподілу.

5.3.2 Визначити диференціальну ентропію нормального розподілу із щільністю ймовірності

.

Як впливає на величину збільшення у два рази а) середнього ; б) дисперсії ?

5.3.3 Визначити ентропію двовимірного рівномірного розподілу, який задано щільністю

5.3.4 Визначити ентропію розподілу (рис. 5.6). Побудувати графік залежності у функції параметра .
	Рис.5.6 Функція розподілу

5.3.5 Визначити диференціальну ентропію випадкової величини, яку задано розподілом

5.3.6 Визначити умовні диференціальні ентропії й для суми нормальних випадкових величин, якщо коефіцієнт кореляції дорівнює .

5.3.7 У результаті дезорганізації керування літаків летять довільними курсами. Після відновлення керування літаки взяли загальний курс із середньоквадратичною помилкою відхилення від курсу . Знайти зміну ентропії, вважаючи, що в першому випадку мав місце рівномірний розподіл ймовірностей, а в другому випадку - нормальний.

5.3.8 Неперервна випадкова величина розподілена за нормальним законом. Вона вимірюється з помилкою , що також відповідає нормальному розподілу. Вихідною величиною є випадкова величина . Чому дорівнює кількість інформації , яка надходить в одиницю часу, якщо й незалежні, середні значення , дисперсії ?

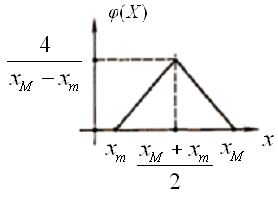
5.3.9 Визначити диференціальну ентропію неперервного повідомлення, розподіленого за законом Симпсона (рис. 5.7):
	Рис.5.7 Розподіл Симпсона

5.3.10 Визначити диференціальну ентропію неперервного повідомлення, розподіленого за законом (а)(рис. 5.8): .
	Рис.5.8 Розподіл (а)

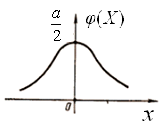
5.3.11 Визначити диференціальну ентропію безперервного повідомлення, що має розподіл Коші (рис. 5.9): .
	Рис.5.9 Розподіл Коші

5.3.12 Визначити диференціальну ентропію випадкової величини, яку задано однобічним експонентним розподілом (рис. 5.10):
	Рис.5.10 Однобічний експонентний розподіл

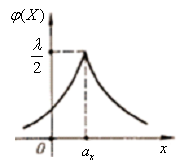
5.3.13 Визначити диференціальну ентропію випадкової величини, яку задано розподілом Лапласа (рис. 5.11): .
	Рис.5.11 Розподіл Лапласа

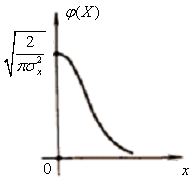
5.3.14 Визначити диференціальну ентропію випадкової величини, яку задано однобічним нормальним розподілом (рис. 5.12):
	Рис.5.12 Однобічний нормальний розподіл

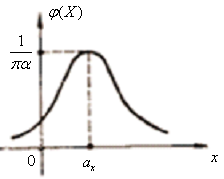
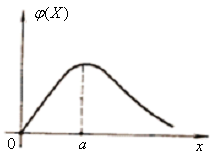
5.3.15 Визначити диференціальну ентропію випадкової величини, яку задано логарифмічним нормальним розподілом (рис. 5.13):
	Рис.5.13 Логарифмічний нормальний розподіл

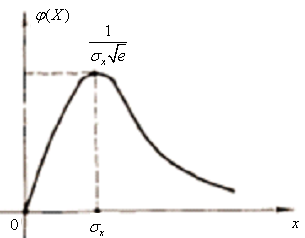
5.3.16 Визначити диференціальну ентропію випадкової величини, яку задано розподілом Релея (рис. 5.14):
	Рис.5.14 Розподіл Релея

5.3.17 Знайти умовні диференціальні ентропії й для суми нормальних і залежних випадкових величин і , якщо їх середньоквадратичне відхилення В, В а коефіцієнт кореляції .

5.3.18 Дві незалежні випадкові погрішності й розподіляються з рівною ймовірністю на інтервалі , де  В. Знайти диференціальну ентропію сумарної погрішності .

5.3.19 Система виміру дальності має дві незалежні тридцятимільйонні випадкові погрішності виміру. Перша випадкова погрішність має при параметрі  м розподіл Симпсона зі щільністю ймовірності

Друга випадкова погрішність рівномірно розподілена на інтервалі зі щільністю ймовірності

Знайти невизначеність результату виміру в середньому на один вимір.

5.3.20 Вимірювальний пристрій має випадкову погрішність виміру , розподілену з параметрами  мВ і  мВ за законом Коші із щільністю ймовірності

.

Знайти середню невизначеність результату виміру.

5.3.21 Знайти середню невизначеність результату виміру координати , якщо випадкова погрішність системи для визначення координат має при середньоквадратичних відхиленнях  мм,  мм і коефіцієнті кореляції нормальний розподіл із щільністю ймовірності

.

5.3.22 Вимірювальний пристрій має випадкову погрішність виміру , яка розподілена з параметрами  мВ^-1 і  мВ за експонентним законом із щільністю ймовірності

.

Знайти середню невизначеність результату виміру.

5.3.23 Інформація передається шляхом зміни амплітуди сигналу , яка розподілена за нормальним законом з параметрами − середнє значення  В та дисперсія  В². Величина виміряється пристроєм, що має погрішність , яка не залежить від амплітуди сигналу і також розподілена за нормальним законом із середнім значенням В та дисперсією В². Визначити кількість інформації про величину , яка міститься в результатах виміру .

5.3.24 Вимірювана величина напруги розподілена з рівною ймовірністю в межах від  В до  В, тобто має щільність імовірності (рис.5.15).

.

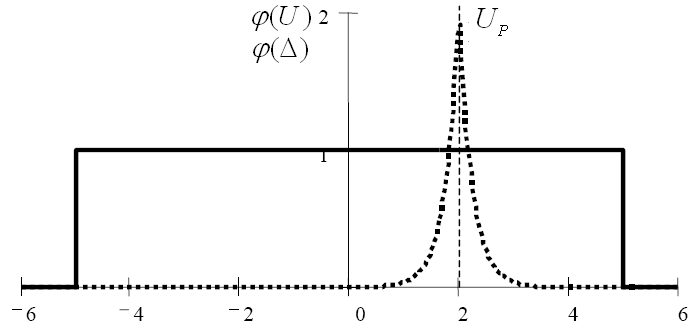
Вимірювальний пристрій для кожного результату виміру має випадкову погрішність , яка розподілена при параметрах  В^-1 і  В за експонентним законом із щільністю ймовірності

.

Знайти кількість інформації, яка отримується в середньому на один вимір.

Рис.5.15 Розподіл напруги

5.3.25 Вимірювана величина має логарифмічно нормальний закон розподілу з параметрами  В,  У та  В із щільністю ймовірності

Погрішність кожного результату виміру (наприклад,  В) при середньоквадратичному відхиленні  В має розподіл модуля нормальної випадкової величини із щільністю ймовірності

Знайти кількість інформації, яка отримується в середньому на один вимір.

5.3.26. На координатній площині об'єкт із рівною ймовірністю може перебувати в будь-якій точці прямокутної площі із центром на початку координат (рис.5.16), де – щільність імовірності положення об'єкту. При цьому координата при параметрі  км змінюється в межах інтервалу , а координата при параметрі  км − у межах інтервалу . Система виміру координат незалежно від їхніх значень (наприклад,  км і  км) при середньоквадратичних відхиленнях  км,  км і коефіцієнті кореляції має нормальний розподіл погрішності із щільністю ймовірності (рис.5.16)

.

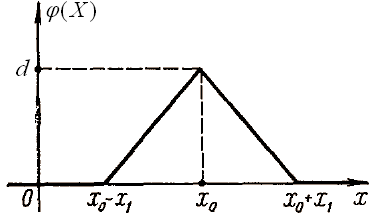
Знайти середню кількість інформації, яку отримаємо в результаті вимірів координат об'єкта.

Рис.5.16 Щільність імовірності положення об'єкта
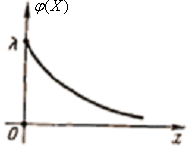