
- •Міністерство освіти і науки україни
- •Методичні вказівки
- •Практичне заняття №1 спектри періодичних сигналів
- •1.1 Мета заняття
- •1.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •1.3 Задачі для самостійної роботи
- •1.4 Контрольні запитання і завдання
- •Практичне заняття №2 спектри неперіодичних сигналів
- •2.1 Мета заняття
- •2.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •2.3 Задачі для самостійної роботи
- •2.4 Контрольні запитання і завдання
- •3.1 Мета заняття
- •3.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,8].
- •3.3 Задачі для самостійної роботи
- •3.4 Контрольні запитання і завдання
- •Практичне заняття №4 ентропія та її властивості
- •4.1 Мета заняття
- •4.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5,7,9].
- •4.3 Задачі для самостійної роботи
- •4.4 Контрольні запитання і завдання
- •Практичне заняття №5 ентропія неперервних джерел інформації
- •5.1 Мета заняття
- •5.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
- •5.3 Задачі для самостійної роботи
- •5.4 Контрольні запитання і завдання
- •Практичне заняття №6 ефективне кодування
- •6.1 Мета заняття
- •6.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •6.3 Задачі для самостійної роботи
- •6.4 Контрольні запитання і завдання
- •Практичне заняття №7
- •7.1 Мета заняття
- •7.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •7.3 Задачі для самостійної роботи
- •7.4 Контрольні запитання і завдання
- •Практичне заняття №8 циклічні коди
- •8.1 Мета заняття
- •8.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
- •8.3 Задачі для самостійної роботи
- •8.4 Контрольні запитання і завдання
- •Навчальне видання методичні вказівки
- •Хнуре. Україна. 61166, Харків, просп. Леніна, 14 Віддруковано в навчально-науковому
- •61166, Харків, просп. Леніна, 14
4.4 Контрольні запитання і завдання
1. Які теоретичні підходи використовують для кількісної оцінки інформації?
2. Що називається ансамблем дискретного джерела повідомлень?
3. Яку міру невизначеності запропонував Хартлі?
4. У якому випадку можна застосувати міру Хартлі?
5. Що називається ентропією дискретного джерела повідомлень?
6. У яких одиницях виміряється ентропія?
7. Перелічити основні властивості ентропії дискретного джерела повідомлень.
8. Що називається умовною ентропією?
9. Перелічити основні властивості умовної ентропії.
10. Чому чисельно дорівнює кількість інформації?
11. Перелічити основні властивості кількості інформації.
Практичне заняття №5 ентропія неперервних джерел інформації
5.1 Мета заняття
Метою заняття є ознайомлення студентів з ентропійними характеристиками неперервних джерел інформації
5.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].
Оцінка невизначеності вибору для неперервного джерела інформації має певну специфіку:
Значення, які реалізуються джерелом інформації, математично відображаються неперервною випадковою величиною.
Імовірності значень цієї випадкової величини не можуть використовуватися для оцінки невизначеності, тому що ймовірність будь-якого конкретного значення дорівнює нулю.
Для оцінки сукупності значень, які
належать до довільного як завгодно
малого інтервалу випадкової величини,
можна використовувати операції
квантування та граничного переходу
(зменшення кванту до нуля). При цьому
використовується щільність розподілу
ймовірності
![]() :
:
|
(5.1) |
Ентропія дискретної випадкової
величини
![]() може
бути записана у вигляді:
може
бути записана у вигляді:
|
(5.2) |
Відомо, що
 ,
тому
,
тому
|
(5.3) |
Якщо
![]() ,
то
,
то
![]() ,
а
,
а
![]() .
.
|
(5.4) |
Друга складова формули (5.4)
при
прагне до нескінченності. Отже, ентропія
безперервного повідомлення також прагне
до нескінченності. Однак у реальних
умовах відлік повідомлень одержувачем
інформації проводиться в дискретних
точках внаслідок кінцевої точності
апаратури, тобто інтервали
![]() мають кінцеву величину;
тому формула (5.4), яка використовується
для знаходження ентропії неперервного
повідомлення має дві складові, одна з
яких обумовлюється законом розподілу
повідомлення, а друга є постійною
величиною, що звичайно виключається з
розгляду.
мають кінцеву величину;
тому формула (5.4), яка використовується
для знаходження ентропії неперервного
повідомлення має дві складові, одна з
яких обумовлюється законом розподілу
повідомлення, а друга є постійною
величиною, що звичайно виключається з
розгляду.
Першу складову (5.4) називають диференціальною ентропією:
|
(5.5) |
Умовна ентропія неперервного джерела інформації дорівнює:
|
(5.6) |
Перша складова формули (5.6) є диференціальною умовною ентропією:
|
(5.7) |
Ця величина характеризує невизначеність вибору випадкової величини за умови, що відомі результати реалізації іншої статистично пов'язаної з нею величиною .
Кількість інформації у неперервних повідомленнях визначається різницею початкової й залишкової ентропій повідомлення:
|
(5.8) |
Приклад 5.1. Визначити диференціальну ентропію неперервного повідомлення, розподіленого за нормальним законом:
|
|
|
|
|
|
Інтеграл від першої складової у отриманому
виразі дорівнює одиниці, тому що
 .
Друга складова визначається наступним
чином:
.
Друга складова визначається наступним
чином:
|
|
Таким чином,
|
|
Приклад 5.2.
Вимірювана величина змінюється у межах
від
![]() до
до
![]() та розподілена рівномірно за законом:
та розподілена рівномірно за законом:
|
|
Знайти диференціальну ентропію:
|
|
Приклад 5.3.
Визначити кількість інформації, яка
міститься в одному вимірі випадкової
величини
,
рівномірно розподіленої в інтервалі
від 0 до 256, якщо погрішність виміру
розподілена за нормальним законом, а
середньоквадратичне значення погрішності
![]() .
.
Диференціальна ентропія випадкової величини :
|
|
Залишкова диференціальна ентропія визначається погрішністю виміру. За аналогією з прикладом 5.2 отримуємо:
|
|
Кількість інформації, яку отримано в результаті одного виміру, визначається різницею початкової й кінцевої ентропій:
|
|
Приклад 5.4.
Знайти спільну ентропію взаємозалежних
повідомлень
і
та умовну ентропію
![]() ,
якщо функція щільності розподілу
відповідає нормальному закону:
,
якщо функція щільності розподілу
відповідає нормальному закону:
|
|
де
![]() – коефіцієнт кореляції значень
і
.
– коефіцієнт кореляції значень
і
.
Спільна диференціальна ентропія й визначається співвідношенням:
|
|
де
|
|
Отже,
|
|
Відомо, що
|
|
тому остаточно отримаємо:
|
|
Застосовуючи формулу (5.7) та
з огляду на те, що
![]() ,
отримаємо значення умовної ентропії
,
отримаємо значення умовної ентропії
|
|
Приклад 5.5.
Випадкова погрішність
![]() вимірювальної
системи, яка складається із двох
пристроїв, є сумою двох незалежних
випадкових погрішностей
вимірювальної
системи, яка складається із двох
пристроїв, є сумою двох незалежних
випадкових погрішностей
![]() і
і
![]() окремих її пристроїв з параметрами
окремих її пристроїв з параметрами
![]() В
и
В
и
![]() В
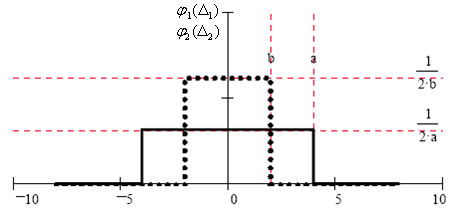
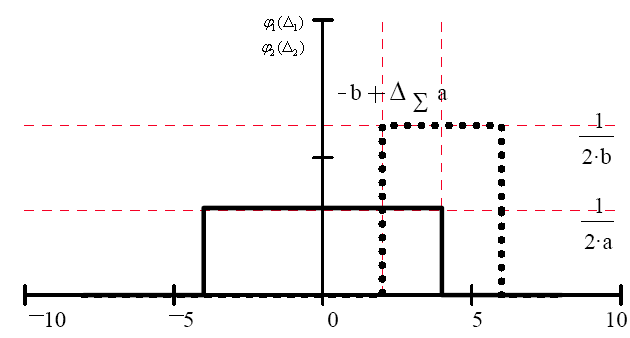
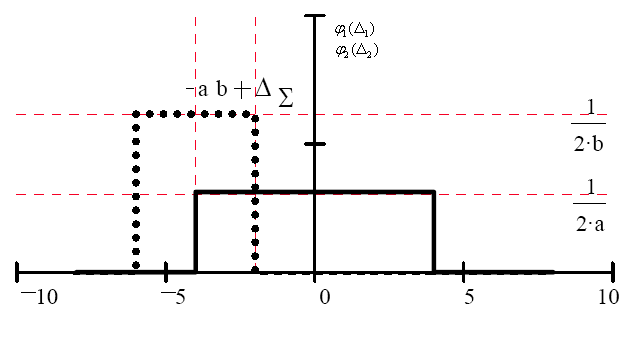
Погрішності мають рівномірні закони
розподілу (рис.5.1) із щільностями
ймовірності відповідно
В
Погрішності мають рівномірні закони
розподілу (рис.5.1) із щільностями
ймовірності відповідно
|
|
|
|
Рис.5.1 Функції розподілу погрішностей |
|
Знайти диференціальну ентропію
сумарної погрішності
![]() .
.
З теорії ймовірностей відомо, що щільність
імовірності
![]() суми двох незалежних випадкових величин
визначається наступним чином:
суми двох незалежних випадкових величин
визначається наступним чином:
|
|
У цьому випадку закон розподілу
суми
називається композицією законів
розподілу складових
![]() й
й
![]() .
.
Таким чином, для рішення задачі необхідно
знайти композицію двох рівномірних
законів розподілу
![]() й
й
![]() ,
тобто:
,
тобто:
|
|
Для обмежених законів розподілу при зсуві щільності ймовірності на величину добуток під знаком інтеграла є відмінним від нуля, коли функції й накладаються одна на одну. У нашому випадку можливі три ситуації.
1) Нехай
![]() і функція
повністю накладається на
(рис.5.2).
і функція
повністю накладається на
(рис.5.2).
|
Рис.5.2 Співвідношення погрішностей (а) |
У цьому випадку інтервал зміни сумарної погрішності визначається нерівністю
|
|
2) Нехай
![]() і функція
частково й праворуч накладається на
(рис.5.3).
і функція
частково й праворуч накладається на
(рис.5.3).
|
Рис.5.3 Співвідношення погрішностей (б) |
У цьому випадку інтервал зміни сумарної погрішності визначається нерівністю
|
|
3) Нехай
![]() і функція
частково й ліворуч накладається на
(рис.5.4).
і функція
частково й ліворуч накладається на
(рис.5.4).
|
Рис.5.4 Співвідношення погрішностей (в) |
У цьому випадку інтервал зміни сумарної погрішності визначається нерівністю
|
|
У результаті інтеграл згортки приймає вигляд
|
|
або після інтегрування
|
|
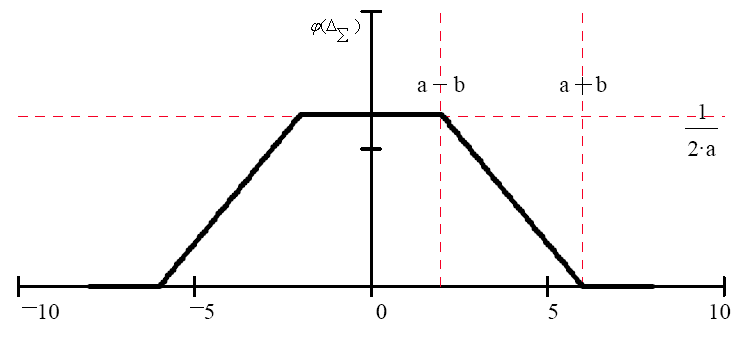
Графік щільності ймовірності сумарної погрішності як композиція законів розподілу доданків і наведено на рис.5.5.
|
Рис.5.5 Графік щільності ймовірності сумарної погрішності |
Для визначення на підставі
(5.5) диференціальної ентропії сумарної
погрішності
необхідно через інтервальну неперервність
функції
![]() обчислити три інтеграли.
обчислити три інтеграли.
Перший інтеграл
|
|
Другий інтеграл
|
|
Третій інтеграл
|
|
Остаточно диференціальна ентропія сумарної погрішності дорівнює:
|
|
|
|
Приклад 5.6.
Потужність випадкового сигналу
на виході аналогового датчику обмежено
при середньоквадратичному відхиленні
![]() В
значенням
В
значенням
![]() .
.
Знайти диференціальний закон розподілу, що забезпечує максимальну відносну ентропію.
Середня потужність стаціонарного
випадкового процесу визначає дисперсію
випадкової величини
в перетині процесу для моменту часу
![]() ,
тобто
,
тобто
![]() .
Таким чином, серед всіх законів розподілу
.
Таким чином, серед всіх законів розподілу
![]() неперервної випадкової величини
з однієї й тією же дисперсією
неперервної випадкової величини
з однієї й тією же дисперсією
![]() необхідно знайти закон розподілу, який
максимізує, згідно з (5.5), наступний
інтеграл:
необхідно знайти закон розподілу, який
максимізує, згідно з (5.5), наступний
інтеграл:
|
|
Відповідно до теореми
варіаційного обчислення для знаходження
функції
![]() ,
яка дає екстремум інтеграла
,
яка дає екстремум інтеграла
|
|
за додаткових умов
|
|
необхідно вирішити рівняння Ейлера
|
|
де  ;
;
![]() - постійні коефіцієнти, які
визначаються за допомогою заданих
додаткових умов.
- постійні коефіцієнти, які
визначаються за допомогою заданих
додаткових умов.
У даному прикладі потрібно знайти максимум інтеграла
|
|
за додаткових умов
|
|
де ![]() - математичне очікування випадкової
величини.
- математичне очікування випадкової
величини.
Отже,
|
|
Тоді рівняння для визначення набуває вигляд
|
|
або після диференціювання
|
|
Рішення рівняння в символічному виді буде наступним
|
|
Якщо позначити![]() ,
то щільність імовірності можна записати
у вигляді
,
то щільність імовірності можна записати
у вигляді
|
|
З додаткових умов знаходимо два рівняння
для визначення постійних
![]() .
Для першої умови, додавши змінну
.
Для першої умови, додавши змінну
![]() при
при
![]() й зважаючи на те, що
й зважаючи на те, що
 отримаємо
отримаємо
|
|
Таким чином, маємо перше рівняння
|
|
Для другої умови, додавши змінну при та двічі виконавши інтегрування вроздріб, отримаємо
|
|
Звідси отримуємо друге рівняння
|
|
Підставляючи в останнє
рівняння величину
![]() з першого рівняння та вирішуючи
друге рівняння, отримаємо
з першого рівняння та вирішуючи
друге рівняння, отримаємо
|
|
Отже, постійні коефіцієнти набувають значення:
|
|
Остаточно щільність імовірності, яка максимізує інтеграл у формулі (5.5), приймає вигляд
|
|
Таким чином, з усіх диференціальних
законів розподілу
з однаковою дисперсією
![]() максимальну відносну
ентропію дає нормальна щільність
імовірності.
максимальну відносну
ентропію дає нормальна щільність
імовірності.

 .
. .
. .
.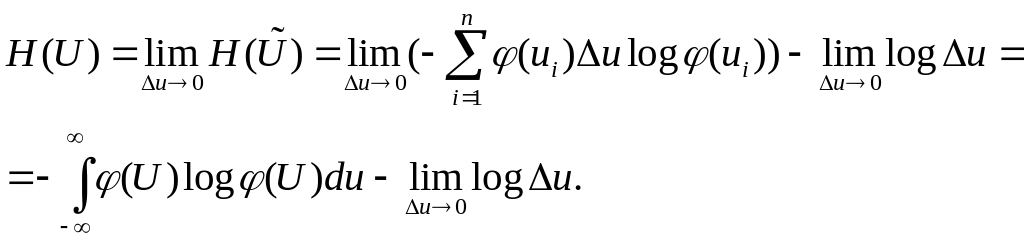
 .
.
 .
.
 .
.
 .
.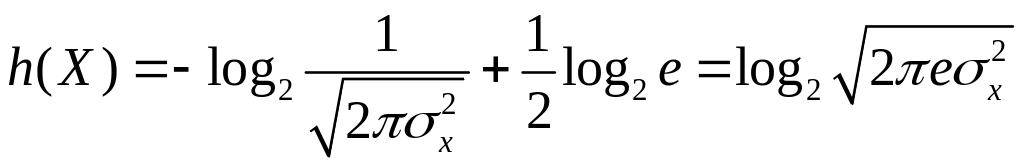 .
.
 .
.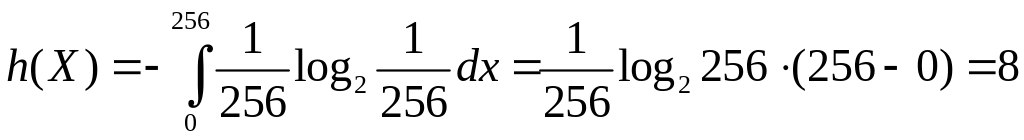 біт.
біт. ,
, ,
, .
.



 .
. і
і

 .
. .
.


 .
. .
. .
. .
. .
.
 ,
, ,
, і
і
 ,
,
 .
. або
або
 .
. .
. .
. .
. и.
и.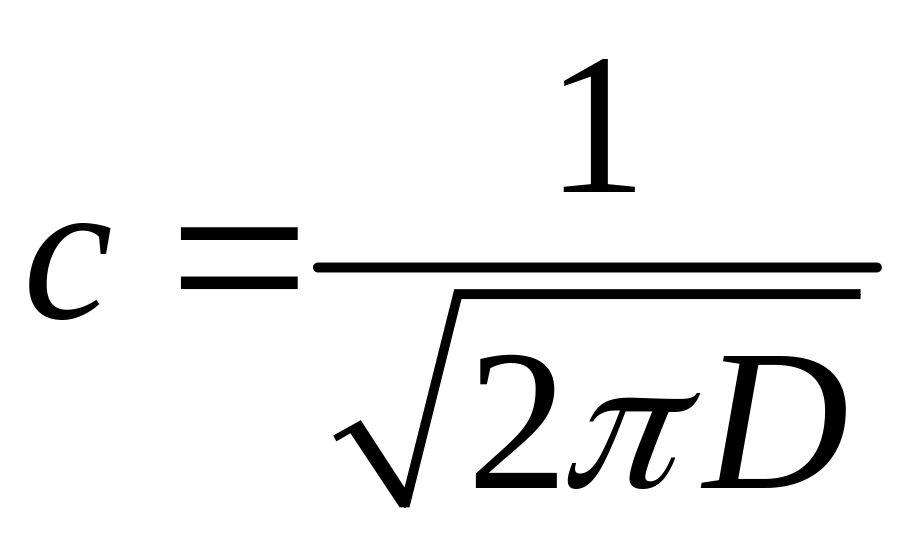
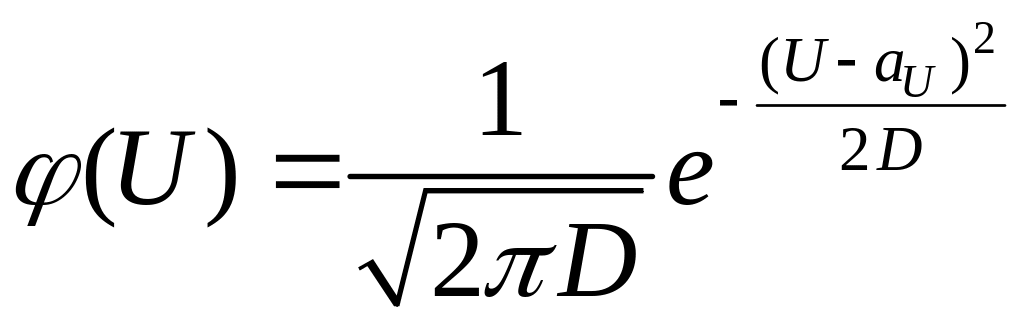 .
.