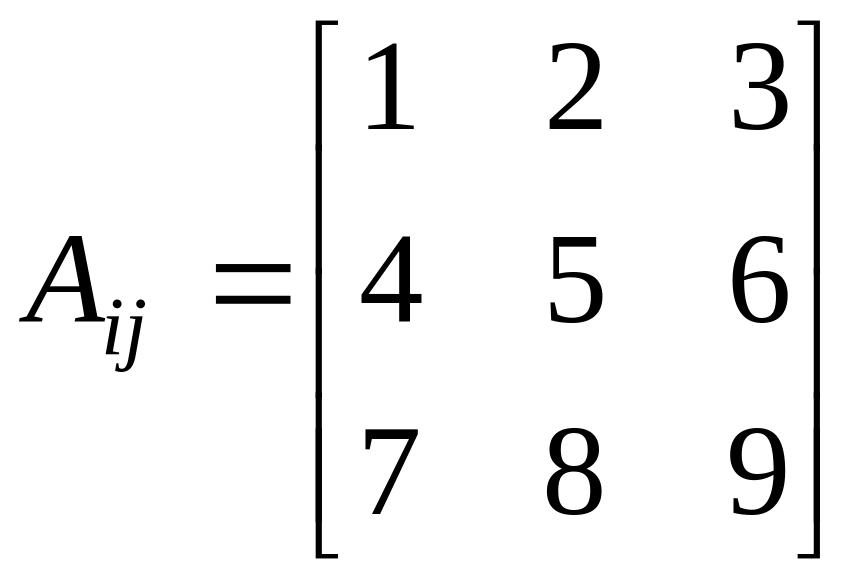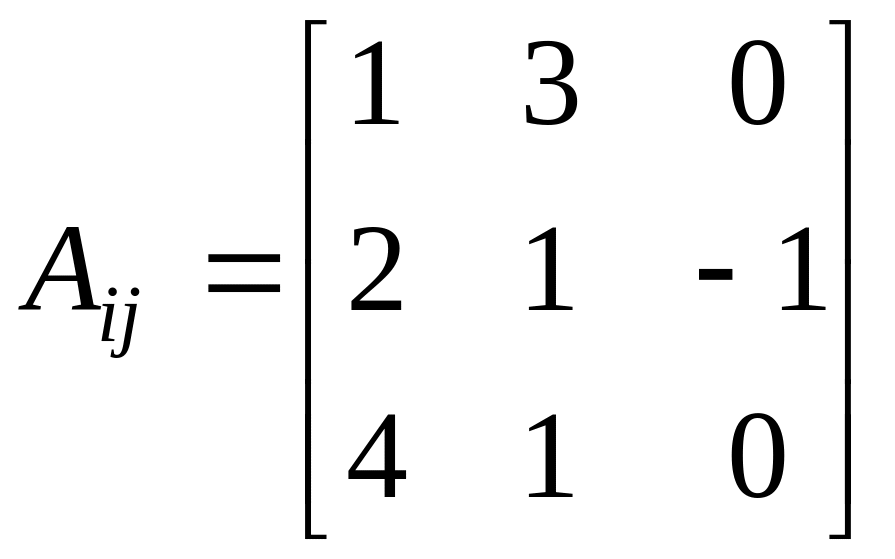- •1. Введение
- •1. Цель работы
- •2. Методы решения прямой задачи кинематики
- •3. Обзор кинематических параметров описания углового и пространственного движения манипулятора
- •3.1. Параметры Эйлера, Крылова, направляющие косинусы. Матрицы преобразования 44
- •3.2. Параметры Родрига – Гамильтона, Кейли – Клейна, кватернионы и их дуальные аналоги
- •3. Обзор методов решения обратной задачи кинематики
- •3.1. Аналитические методы
- •3.2. Численные методы
- •5. Приложение 1. Пример использования различных кинематических параметров
- •5.1. Матрицы направляющих косинусов
- •5.2. Кватернионы (кватернионные матрицы)
- •5.3. Параметры Кейли-Клейна
- •6. Приложение 2. Пример решение прямой и обратной задачи для манипулятора типа puma
- •7. Контрольные вопросы
- •8. Задания для выполнения лабораторно-исследовательской работы Задание 1
- •Задание 2
- •Задание 3
- •9. Содержание отчета о работе
- •Литература
7. Контрольные вопросы
Перечислите методы решения прямой задачи кинематики.
Какие кинематические параметры описания движения манипулятора вы знаете ?
Сформулируйте обратную задачу кинематики и перечислите методы ее решения.
В чем заключается метод решения обратной задачи кинематики в явном виде матричным методом
Почему решение обратной задачи кинематики получить сложнее по - сравнению с получением решения прямой задачи ?
В чем сложность получения решения обратной задачи кинематики для избыточных манипуляторов ?
Перечислите оптимизационные методы решения обратной задачи кинематики. Какой вид будет иметь целевая функция ?
8. Задания для выполнения лабораторно-исследовательской работы Задание 1
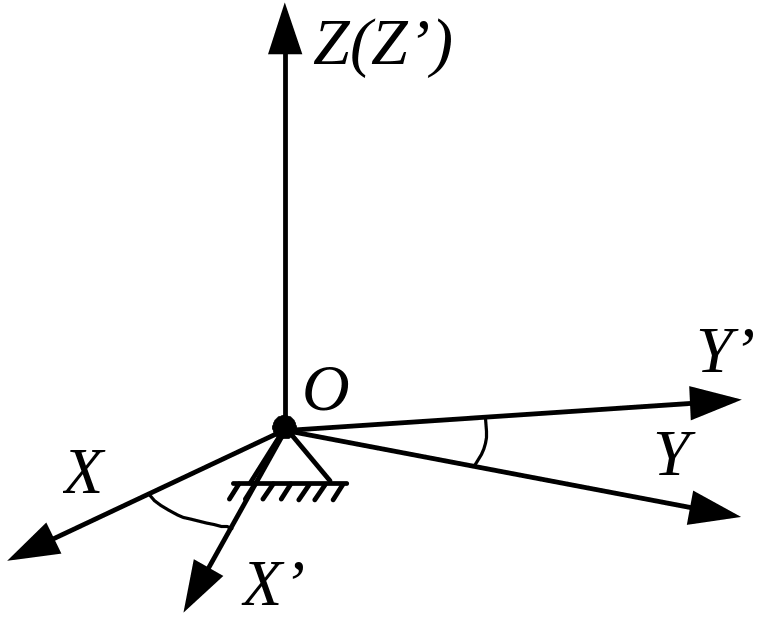
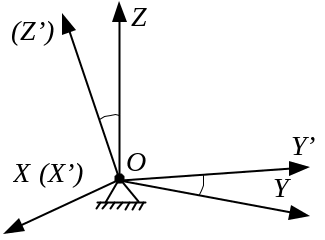
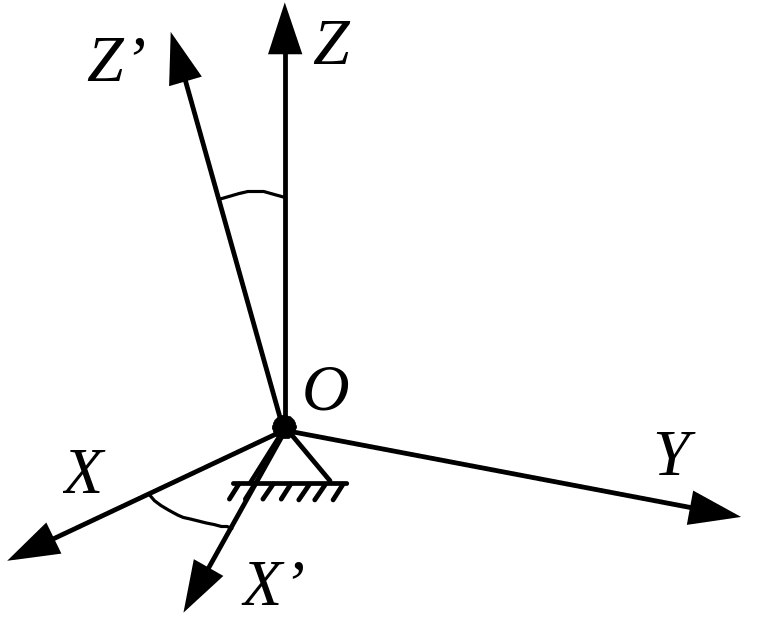
1. Твердое тело с закрепленное в точке О поворачивают вокруг оси Z системы координат XYZ. Необходимо составить матрицу поворота подвижной системы координат X’Y’Z’ относительно каждой из трех осей (рис.1). |
|
2. Твердое тело с закрепленное в точке О поворачивают вокруг оси X системы координат XYZ. Необходимо составить матрицу поворота подвижной системы координат X’Y’Z’ относительно каждой из трех осей (рис.1). |
|
3. Твердое тело с закрепленное в точке О поворачивают вокруг оси Y системы координат XYZ. Необходимо составить матрицу поворота подвижной системы координат X’Y’Z’ относительно каждой из трех осей (рис.1). |
|
4. Выразить координаты точки М в базовой системе координат XYZ при ее повороте на угол вокруг оси X в виде x’ = fx (x,y,z,), y’ = fy (x,y,z,), z’ = fz (x,y,z,). 5. В повернутой системе координат X’Y’Z’ заданы две точки а = (4,3,2)т и b = (6,2,4)т. Требуется определить координаты этих точек в базовой системе координат, если система координат X’Y’Z’ повернута относительно оси X на 60 и относительно оси Y - на 30. |
|
6. По известным координатам точек а = (4,3,2)т и b = (6,2,4)т в базовой системе координат XYZ требуется определить соответствующие координаты в системе координат X’Y’Z’, повернутой относительно оси Z и X на 60 и 45 соответственно. |
|
7. Разработать программу, позволяющую получить результирующую матрицу преобразования в результате поворотов на углы Эйлера и углы Крылова. |
|
8. Разработать программу, осуществляющую перемножение матриц элементарных поворотов и перемещений в соответствии со схемой Денавитта-Хартенберга. Входные параметры – смещения вдоль осей Z и X и повороты вокруг тех же осей. |
|
9. Две точки аx’y’z’ = (4,3,2)т и bx’y’z’ = (6,2,4)т требуется сместить на +5 единиц вдоль оси X и на – 3 единицы вдоль Z. Используя соответствующую однородную матрицу преобразования получить координаты точек аxyz и bxyz , полученных в результате этих смещений. |
|
10. Требуется определить матрицу Т, задающую преобразование, состоящее из поворота на угол вокруг оси X, затем смещения на b единиц вдоль повернутой оси Y’. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

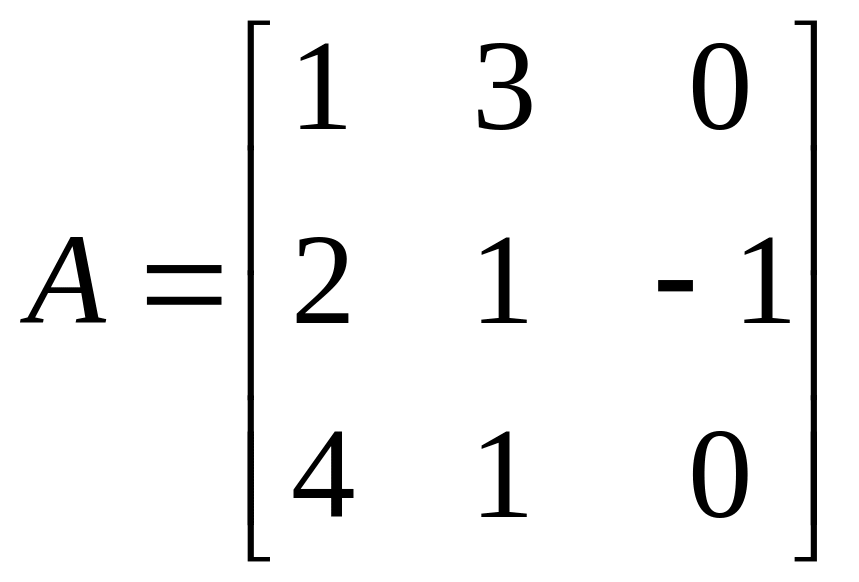 найти их произведение b
= A
a
найти их произведение b
= A
a