- •1. Введение
- •1. Цель работы
- •2. Методы решения прямой задачи кинематики
- •3. Обзор кинематических параметров описания углового и пространственного движения манипулятора
- •3.1. Параметры Эйлера, Крылова, направляющие косинусы. Матрицы преобразования 44
- •3.2. Параметры Родрига – Гамильтона, Кейли – Клейна, кватернионы и их дуальные аналоги
- •3. Обзор методов решения обратной задачи кинематики
- •3.1. Аналитические методы
- •3.2. Численные методы
- •5. Приложение 1. Пример использования различных кинематических параметров
- •5.1. Матрицы направляющих косинусов
- •5.2. Кватернионы (кватернионные матрицы)
- •5.3. Параметры Кейли-Клейна
- •6. Приложение 2. Пример решение прямой и обратной задачи для манипулятора типа puma
- •7. Контрольные вопросы
- •8. Задания для выполнения лабораторно-исследовательской работы Задание 1
- •Задание 2
- •Задание 3
- •9. Содержание отчета о работе
- •Литература
5.3. Параметры Кейли-Клейна
Параметры Кейли-Клейна представляют собой комплексно-сопряженные комбинации параметров Родрига-Гамильтона, составляющих кватерниона, и имеют вид
|
(55) |
Матрица перехода между соседними звеньями (66) составлена из элементов (65)
|
(56) |
Таким образом, в результате последовательного перемещения от одного звена к другому будут получены матрицы перехода вида (56), которые будучи перемноженными между собой в том же порядке дадут результирующую матрицу, связывающую основание манипулятора с последним звеном.
При
совмещении систем координат выше были
получены кватернионы, соответствующие
элементарным плоским поворотам. Их и
будем использовать для составления
матриц перехода. Переход
можно описать двумя кватернионами:
![]() ;
2)
.
;
2)
.
В результате чего можно составить две матрицы перехода
|
|
|
(57) |
Переход
![]()
описан через кватернион вращения
описан через кватернион вращения
![]() ,
откуда
,
откуда
|
(58) |
Так как при переходе от системы координат к кватернион аналогичен кватерниону , то получим
|
(59) |
В результате перемножения полученных матриц перехода (56) - (59), результирующая матрица будет иметь вид:
|
|
и в окончательном виде, получим:
|
(60) |
6. Приложение 2. Пример решение прямой и обратной задачи для манипулятора типа puma
Для рассматриваемого манипулятора были получены уравнения решения прямой и обратной задач кинематики, приведенные ниже. Переход от базовой системы координат к системе координат, связанной с захватом, осуществлялся в соответствии с представлением Денавита – Хартенберга. Повороты и перемещения, описывающие движение каждого звена указаны в таблице 1, в соответствии с ними построена матрица преобразования T (61).
Таблица 1
Параметры систем координат звеньев манипулятора |
|||||
i |
|
|
|
|
|
1 |
|
90 |
0 |
0 |
|
2 |
|
0 |
|
0 |
|
3 |
|
0 |
|
0 |
|
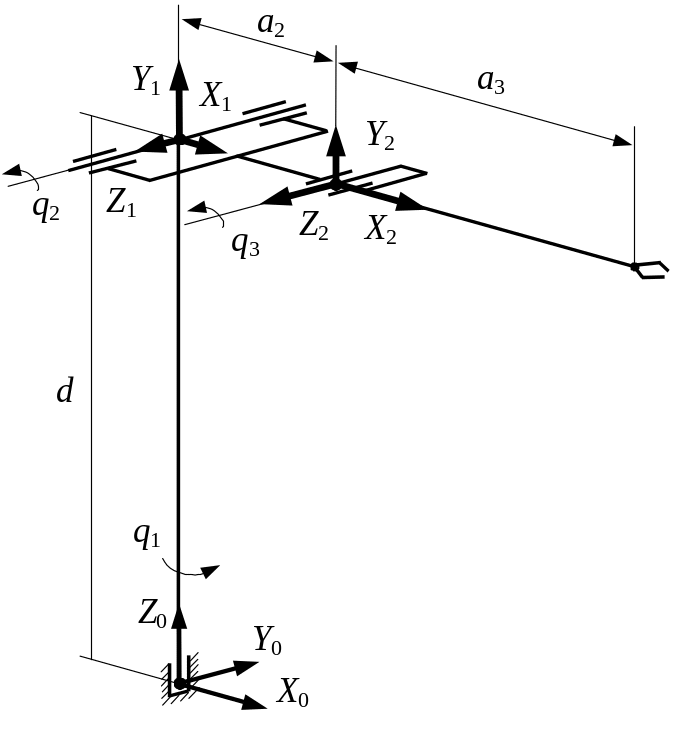
Рис. 9. Общий вид типового трехзвенного манипулятора |
Рис. 10. Кинематическая схема трехзвенного манипулятора |
||||
|
(61) |
Прямые и обратные уравнения кинематики приведены в уравнениях (62) и (63) соответственно.
|
(62) |
|
(63) |
Знак
в выражении для
![]() обозначает общую конфигурацию руки
робота. Положительное значение
соответствует решению, при котором
локоть направлен книзу, отрицательное
– когда локоть направлен кверху.
обозначает общую конфигурацию руки
робота. Положительное значение
соответствует решению, при котором
локоть направлен книзу, отрицательное
– когда локоть направлен кверху.
В
Рис.
11. Неопределенность,
возникающая
при решении
обратной задачи кинематики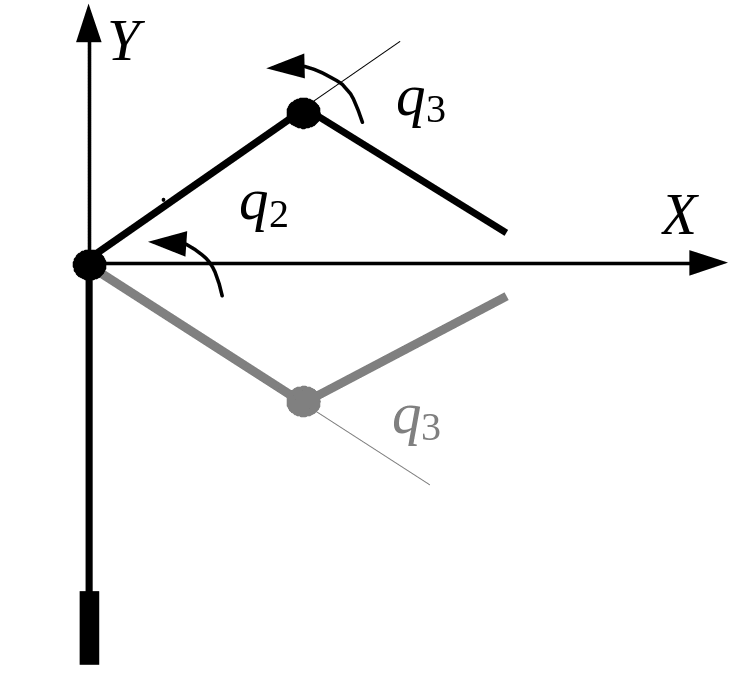

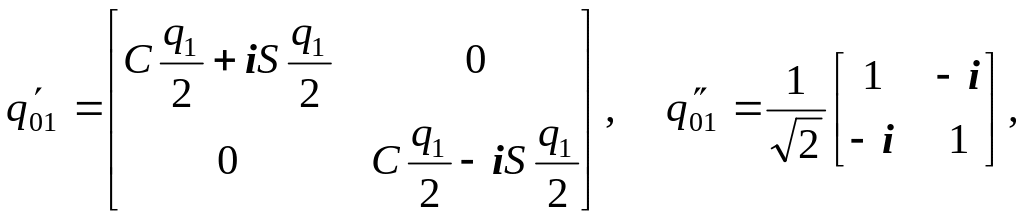
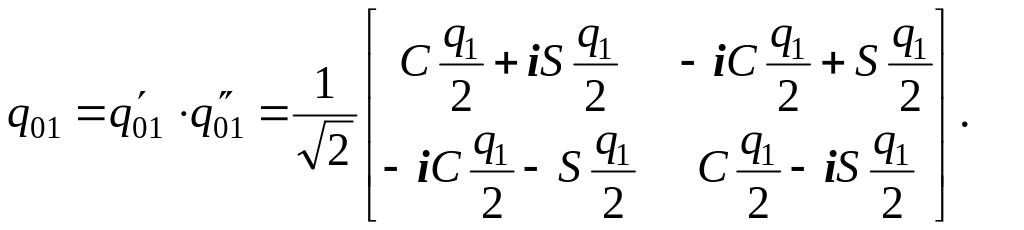
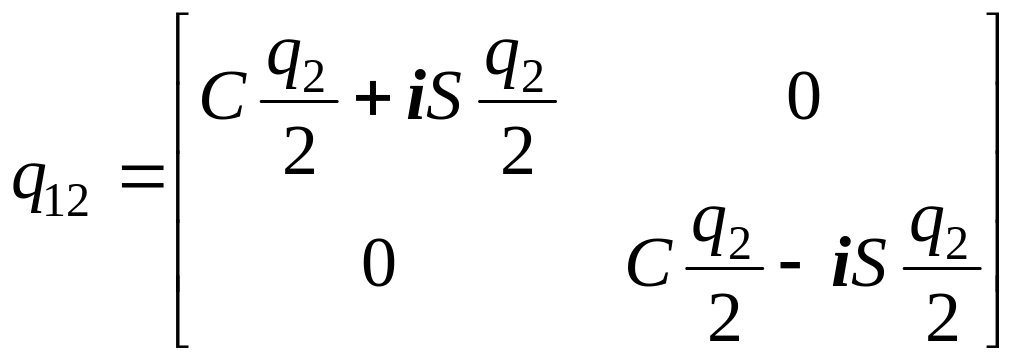 .
.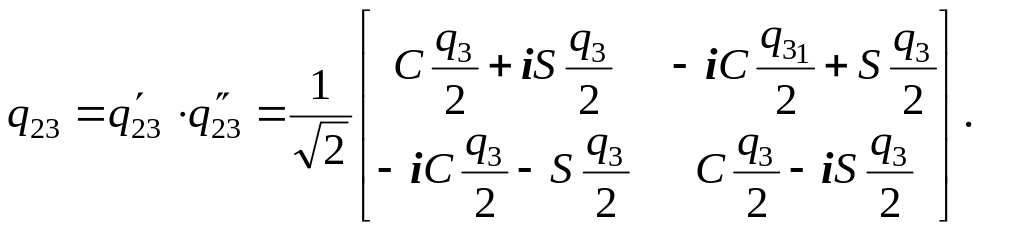
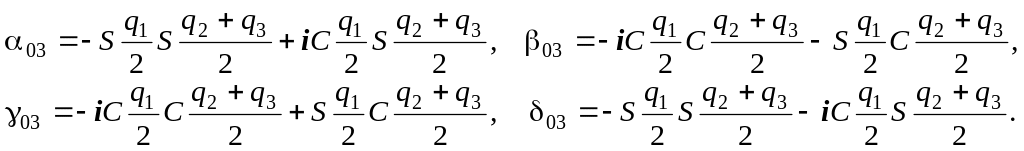

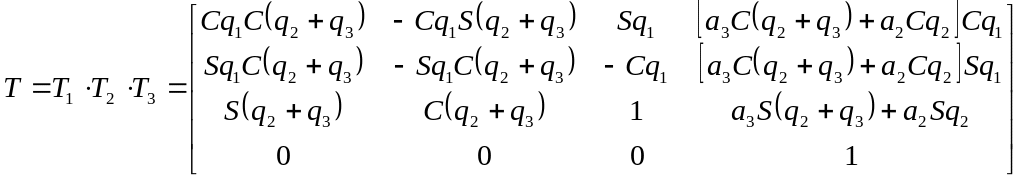
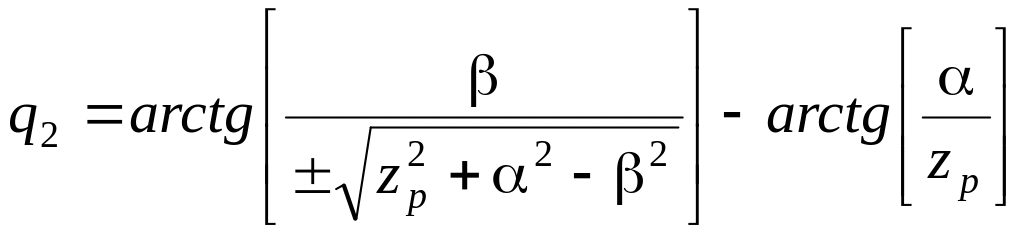 ;
;