
- •1. Введение
- •1. Цель работы
- •2. Методы решения прямой задачи кинематики
- •3. Обзор кинематических параметров описания углового и пространственного движения манипулятора
- •3.1. Параметры Эйлера, Крылова, направляющие косинусы. Матрицы преобразования 44
- •3.2. Параметры Родрига – Гамильтона, Кейли – Клейна, кватернионы и их дуальные аналоги
- •3. Обзор методов решения обратной задачи кинематики
- •3.1. Аналитические методы
- •3.2. Численные методы
- •5. Приложение 1. Пример использования различных кинематических параметров
- •5.1. Матрицы направляющих косинусов
- •5.2. Кватернионы (кватернионные матрицы)
- •5.3. Параметры Кейли-Клейна
- •6. Приложение 2. Пример решение прямой и обратной задачи для манипулятора типа puma
- •7. Контрольные вопросы
- •8. Задания для выполнения лабораторно-исследовательской работы Задание 1
- •Задание 2
- •Задание 3
- •9. Содержание отчета о работе
- •Литература
3.2. Параметры Родрига – Гамильтона, Кейли – Клейна, кватернионы и их дуальные аналоги
В соответствии с теоремой Эйлера – Даламбера твердое тело с одной закрепленной точкой может быть переведено из любого начального положения в любое конечное с помощью одного поворота вокруг некоторой оси, которая называется осью Эйлера (рис. 4). Поворот можно описать выражением (12),
|
(12) |
г
Рис.
4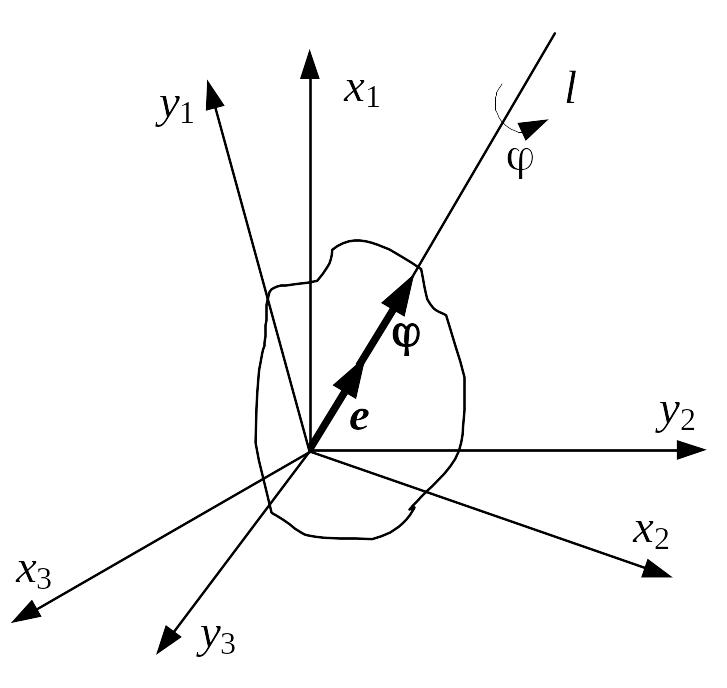
![]() -
единичный вектор эйлеровой оси, .
-
единичный вектор эйлеровой оси, .![]() - угол поворота
- угол поворота
Таким
образом, для описания вращательного
движения ТТ используется четыре параметра
![]() ,
где
,
где
![]() -
проекция на соответствующую ось
координат. Четвертым уравнением –
является уравнение связи, имеющее
следующий вид:
-
проекция на соответствующую ось
координат. Четвертым уравнением –
является уравнение связи, имеющее
следующий вид:
![]() (13)
(13)
В теории конечного поворота вектор (12) называется вектором истинного Эйлерова поворота. Попытка использования указанного параметра для описания вращательного движения ТТ показала, что он приводит к появлению достаточно неудобных и громоздких выражений, поэтому в дальнейшем вместо вектора (12) было предложено использовать другой, пропорциональный ему вектор который назван вектором конечного поворота:
|
(14) |
Вектор конечного поворота (14) позволяет получить значительно более простые и компактные уравнения кинематики.
Для
решения конкретных задач кинематики
обычно требуются проекции вектора (14)
на координатные оси. Обозначив проекции
векторы
![]() на координатные оси
на координатные оси
![]() через
через
![]() ,
и углы между вектором
и соответствующими осями через
,
и углы между вектором
и соответствующими осями через
![]() ,
можно записать
,
можно записать
|
(15) |
Вектор
и его проекции
![]() не нашли широкого применения в механике,
так как в последствии были предложены
другие, более удобные параметры, которые
получаются непосредственно из выражений
(14) и (15).
не нашли широкого применения в механике,
так как в последствии были предложены
другие, более удобные параметры, которые
получаются непосредственно из выражений
(14) и (15).
В теории конечного поворота для описания вращательного движения вместо величин более удобными оказались пропорциональные им величины, названные параметрами Эйлера (Родрига - Гамильтона) (16):
|
(16) |
Их
отличием от предыдущих параметров
является то, что они позволяют придать
уравнения кинематики более симметричный
вид. В выражение (16) введен коэффициент
пропорциональности
![]() .
Воспользовавшись уравнением нормирования
(17)
можно показать, что
определяется выражением (18)
.
Воспользовавшись уравнением нормирования
(17)
можно показать, что
определяется выражением (18)
|
(17) |
|
(18) |
Если в уравнение (16) подставить (17) с учетом (16), то окончательно можно получить:
|
(19) |
Таким образом, для описания вращательного движения ТТ можно использовать четыре параметра Эйлера, которые обладают следующими достоинствами: 1) в отличие от углов Эйлера (Крылова) они во многих случаях позволяют избавиться от операций с тригонометрическими функциями, что повышает эффективность использования ЭВМ при решении задач; 2) кинематические уравнения в параметрах Эйлера (Родрига – Гамильтона) являются линейными уравнениями, которые не вырождаются при любом угловом положении ТТ, в сравнение: аналогичные уравнения в углах Эйлера нелинейны и имеют особые точки.
Рассмотрим параметры Кейли-Клейна и кватернионы, составляющими которых являются параметры Родрига – Гамильтона.
Параметры Кейли – Клейна в настоящее время особенно широко используются для описания вращательного движения в квантовой механике. В обычной механике сравнительно редко. Эти параметры представляют собой комплексные комбинации параметров Родрига –Гамильтона и имеют следующий вид:
|
(20) |
Видно, что параметры Кейли –Клейна попарно представляют собой комплексно – сопряженные числа, поэтому они связаны следующим соотношением:
|
(21) |
С геометрической точки зрения, при помощи параметров Кейли –Клейна повороту ТТ ставиться в соответствие некоторое дробно – линейное преобразование в плоскости комплексного переменного
|
(22) |
Смысл выражения (22) состоит в том, что в случае задания поворота параметрами Кейли – Клейна координата z после поворота переходит в координату z.
Использование в механике параметров Эйлера в дальнейшем привело к тому, что на их основе были образованы новые параметры, получившие название кватернионов.
Кватернион представляет собой гиперкомплексное число следующего вида:
|
(23) |
где
![]() - определяются выражением (19).
- определяются выражением (19).
Свойства и алгебра кватернионов достаточно широко представлены в литературе [4].
Нужно отметить, что кватерниону поворота (23) можно поставить в соответствие кватернионные матрицы размерностью 44, при этом для описания вращательного движения используется хорошо разработанный аппарат матричной алгебры, а матрицы компонуются из четырех параметров Эйлера, что делает описание более компактным в сравнении, например, с методом направляющих косинусов, где используется 9 различных параметров.
Для
описания вращательного движения можно
использовать кватернионные матрицы
двух типов
![]() ,
либо
,
либо
![]() (24), а в случае если в алгоритме часто
используется коммутативное произведение
матриц, то иногда удобно использовать
одновременно обе матрицы.
(24), а в случае если в алгоритме часто
используется коммутативное произведение
матриц, то иногда удобно использовать
одновременно обе матрицы.
|
(24) |
Описание произвольного пространственного движения с помощью нетрадиционных параметров возможно при использовании теории дуальных чисел.
Дуальным числом называют число, которое может быть представлено в следующем виде:
|
(25) |
где а
– главная часть,
![]() - комплексная (моментная) части дуального
числа, причем
- комплексная (моментная) части дуального
числа, причем
![]() - вещественные числа, а
- вещественные числа, а
![]() - комплексность Клиффорда, такая, что
- комплексность Клиффорда, такая, что
![]() .
.
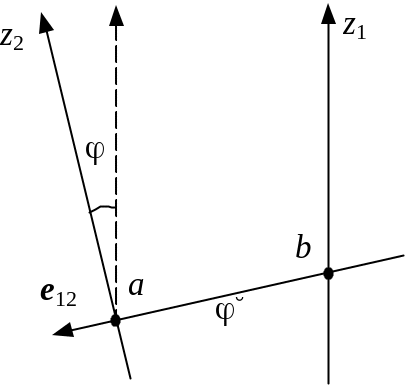
Дуальным углом между двумя осями, произвольно расположенными в пространстве, называют фигуру, которая образована данными осями и отрезками прямой, пересекающим эти оси под прямым углом (рис. 5).
Обозначим
через аb
кратчайшее расстояние между осями,
![]() и
и
![]() .
Тогда дуальный угол
будет иметь вид:
.
Тогда дуальный угол
будет иметь вид:
|
(26) |
здесь
-
угол между осями
![]() и
и
![]() ,
а
,
а
![]() - кратчайшее расстояние между осями.
Положительное направление определяется
направлением
- кратчайшее расстояние между осями.
Положительное направление определяется
направлением
![]() .
.
Таким образом, дуальный угол позволяет описывать одним числом совокупность поступательного и вращательного движения, поскольку переход от к z2 в пространстве может быть осуществлен за счет совокупности двух движений. Все кинематические параметры, применяемые для углового движения можно использовать для описания пространственного движения, если их элементы заменить дуальными величинами.
Таким образом, в случае произвольного пространственного движения для вектора конечного перемещения получим винт конечного перемещения. Параметры Эйлера (Родрига – Гамильтона) заменят их дуальные аналоги, аналогично получим дуальные параметры Кейли – Клейна и дуальные кватернионы, называемые бикватернионами.
Рис. 5 |
Рис. 6 |
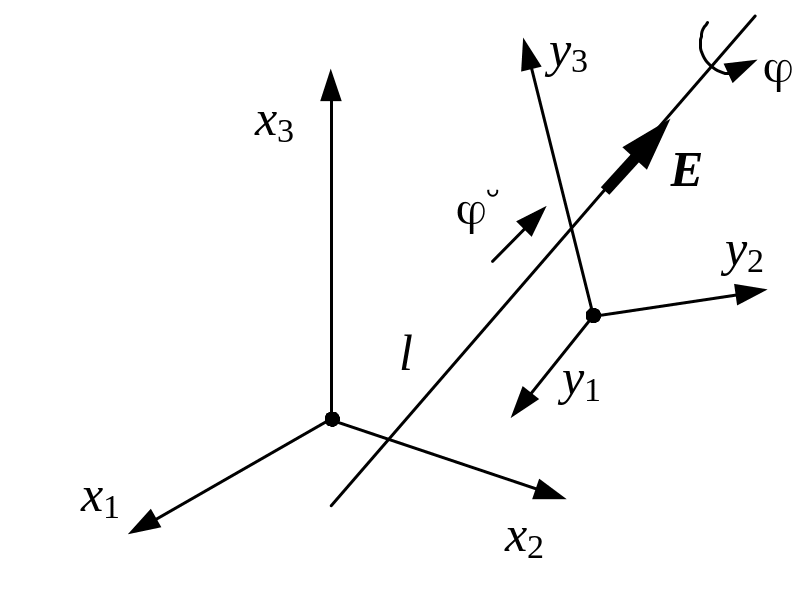
По
теореме Шалля ТТ может быть переведено
из любого начального положения в любое
конечное с помощью одного винтового
перемещения
![]() (рис. 6). Таким образом, вместо вектора
конечного перемещения (14) можно записать
винт конечного перемещения (27)
(рис. 6). Таким образом, вместо вектора
конечного перемещения (14) можно записать
винт конечного перемещения (27)
|
(27) |
И для проекций винта получим
|
(28) |
угол
![]() - угол между прямой l
и i-ой
координатной осью
- угол между прямой l
и i-ой
координатной осью
Дуальные параметры Эйлера (Родрига – Гамильтона) по аналогии с обычными параметрами можно выразить следующими соотношениями:
|
(29) |
Дуальные параметры Кейли- Клейна будут иметь вид (30)
|
(30) |
Бикватернионы, предложенные Клиффордом, позволяют описывать пространственное движение в более удобной и компактной форме. Бикватернион вводится по аналогии с обычным кватернионом, при этом вещественные параметры заменяются их дуальными аналогами.
|
(31) |
где
![]() - обычные вещественные параметры Эйлера,
- обычные вещественные параметры Эйлера,
![]() - параметры винтового движения.
Бикватернионная матрица имеет следующий
вид:
- параметры винтового движения.
Бикватернионная матрица имеет следующий
вид:
|
(32) |

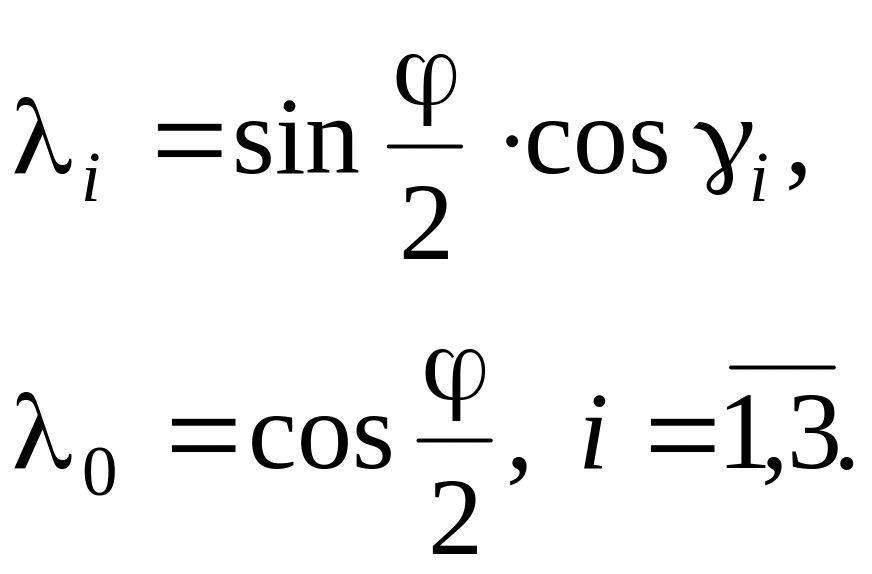
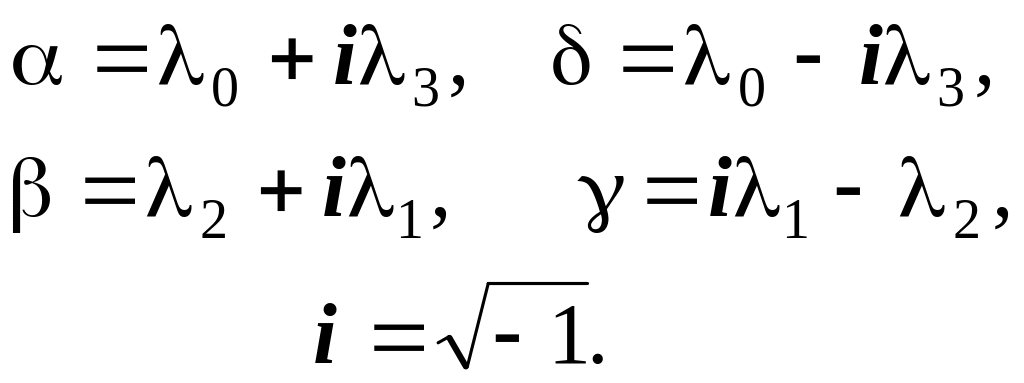
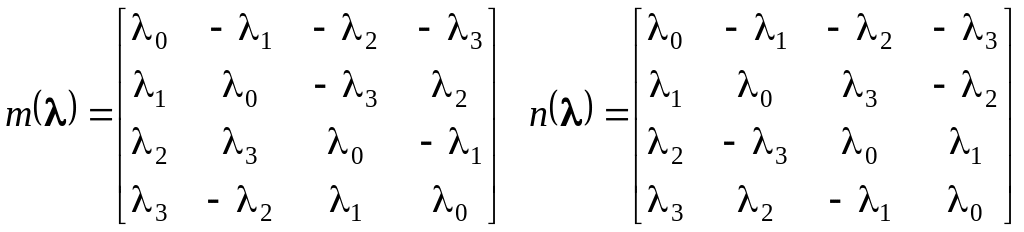 .
.
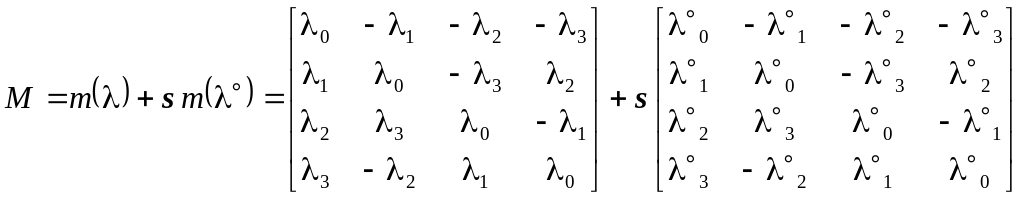 .
.