
- •Содержание
- •Введение
- •1. Требования к знаниям, умениям и навыкам для выполнения
- •2.1. Лабораторная работа №1
- •Методические рекомендации и выполнение.
- •2.2. Лабораторная работа №2
- •2.3.Лабораторная работа №3
- •2. Проанализировать линейные коэффициенты парной и частной корреляции.
- •Входной интервал х – диапазон, содержащий данные факторов независимого признака
- •2. Проанализировать линейные коэффициенты парной и частной корреляции.
- •2.4.Лабораторная работа №4
- •2.5. Лабораторная работа №5
- •Литература
- •Приложения
- •1. Критические значения t – критерия Стьюдента при уровне значимости 0,01, 0,05, 0,01 (двухсторонний)
- •3 Значения статистик Дарбина – Уотсона dL, dU при уровне значимости 0,05
2.2. Лабораторная работа №2
Построение модели нелинейной парной регрессии, анализ статистической значимости и выполнение прогноза
Цель: провести спецификацию модели; оценить параметры линеаризованного уравнения показательной парной регрессии; проанализировать статистическую значимость показательного уравнения парной регрессии; оценить тесноту связи фактора с результативным признаком; выполнить прогнозирование; интерпретировать результаты; проверить полученные результаты с помощью ППП MS Excel.
Теоретические сведения
Парная регрессия – уравнение связи двух переменных у и х: ,
где у – зависимая переменная (результативный признак);х – независимая, объясняющая переменная (признак - фактор).Различают линейные и нелинейные регрессии. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
- полиномы разных
степеней
![]()
- равносторонняя
гипербола
![]()
Регрессии, нелинейные по оцениваемым параметрам:
- степенная
![]()
- показательная
![]()
- экспоненциальная
![]()
При оценке параметров нелинейных регрессий используют МНК, предварительно преобразовывая уравнение к линейному виду:
- для равносторонней
гиперболы вида
![]() ,
заменив
,
заменив
![]() на z,
получим линейное уравнение регрессии:
на z,
получим линейное уравнение регрессии:
![]() и система нормальных уравнений составит:
и система нормальных уравнений составит:

- для полулогарифмической
кривой
![]() ,
заменив lnx
на z,
получим линейное уравнение регрессии
,
заменив lnx
на z,
получим линейное уравнение регрессии
![]()
Регрессии, нелинейные
по оцениваемым параметрам, подразделяются
на два типа: нелинейные модели внутренне
линейные и нелинейные модели внутренне
нелинейные. Если нелинейная модель
внутренне линейна, то она с помощью
логарифмирования уравнения по основанию
e
или 10 может быть приведена к линейному
виду. Например, для оценки параметров
степенной функции
![]() применяется метод наименьших квадратов
к линеаризованному уравнению
применяется метод наименьших квадратов
к линеаризованному уравнению
![]() ,
т.е. решается система нормальных
уравнений:
,
т.е. решается система нормальных
уравнений:
 .
.
Параметр
![]() определяется непосредственно из системы,
а параметр а – косвенным путем после
потенцирования величины lnа.
определяется непосредственно из системы,
а параметр а – косвенным путем после
потенцирования величины lnа.
Нелинейная модель
внутренне нелинейная (например,
![]() )
не может быть преобразована в уравнение,
линейное по коэффициентам. Для оценки
параметров в этом случае используют
итеративные процедуры.
)
не может быть преобразована в уравнение,
линейное по коэффициентам. Для оценки
параметров в этом случае используют
итеративные процедуры.
Тесноту связи
изучаемых явлений оценивает индекс
корреляции
![]() для нелинейной регрессии
для нелинейной регрессии
![]() :
:
 ,
,
где![]() общая дисперсия результативного признака
общая дисперсия результативного признака
![]() - остаточная дисперсия, определяемая
исходя из уравнения регрессии
- остаточная дисперсия, определяемая
исходя из уравнения регрессии
![]()
Для оценки качества подбора функции рассчитывается квадрат индекса корреляции, называемый индексом детерминации. Индекс детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака: .
Коэффициент эластичности, средняя ошибка аппроксимации определяются аналогично линейной парной регрессии (см. лабораторную работу №1).
Оценка значимости уравнения нелинейной парной регрессии в целом дается с помощью F – критерии Фишера и выполняется аналогично оценке значимости уравнения линейной парной регрессии (см. лабораторную работу №1).
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения . Вычисляется средняя стандартная ошибка прогноза:
, где . и строится доверительный интервал прогноза, границы которого определяются как предельная ошибка прогноза.
Постановка задачи
По территориям региона приводятся данные за 199Х год (табл.6).
Таблица 6
№ региона |
Среднедушевой прожиточный минимум в день , руб.,x |
Среднедневная заработная плата , руб., y |
1 |
2 |
3 |
1 |
78 |
133 |
2 |
82 |
148 |
3 |
87 |
134 |
4 |
79 |
154 |
Продолжение таблицы 6
1 |
2 |
3 |
5 |
89 |
162 |
6 |
106 |
195 |
7 |
67 |
139 |
8 |
88 |
158 |
9 |
73 |
152 |
10 |
87 |
162 |
11 |
76 |
159 |
12 |
115 |
173 |
Требуется:
Для характеристики зависимости y от x:
а) построить показательное уравнение парной регрессии у от х;
б) оценить тесноту связи с помощью индексов корреляции и детерминации;
в) оценить качество показательного уравнения парной регрессии с помощью средней ошибки аппроксимации;
г) дать оценку силы связи с помощью среднего коэффициента эластичности;
д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера.
е) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости =0,05 .
2. Проверить полученные результаты с помощью ППП MS Excel.
Методические рекомендации и выполнение
1. а) Построению показательной модели y=a·bx предшествует процедура линеаризации переменных. Логарифмируя обе части уравнения , получим:
ln y = ln a+
x·lnb . Введем
обозначения :
![]() ,
,
![]() ,
,
![]() .Тогда
уравнение запишется в виде:
.Тогда
уравнение запишется в виде:
![]() .Параметры
полученной линейной модели рассчитываем
аналогично тому, как это было сделано
в лабораторной работе № 1. Используем
данные расчетной таблицы 7
.Параметры
полученной линейной модели рассчитываем
аналогично тому, как это было сделано
в лабораторной работе № 1. Используем
данные расчетной таблицы 7
Таблица 7

Построим линейное
уравнение парной регрессии Y
по х.
Используя данные таблицы 7, имеем:
![]() ,
,
![]() .
.
Получим линейное
уравнение регрессии:
![]() .
.
Проведя потенцирование уравнения, получим искомую нелинейную показательную модель:
![]() .
.
б) Для расчета
индекса корреляции
![]() нелинейной регрессии воспользуемся
таблицу 7
нелинейной регрессии воспользуемся
таблицу 7  .
.
Найдем индекс
детерминации:
![]() .
.
Это означает, что 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума.
в) Для оценки качества полученной модели
найдем среднюю ошибку аппроксимации:
![]() .
.
В среднем, расчетные значения отклоняются от фактических на 5,851%. Качество построенной модели оценивается как хорошее, т.к. значение – менее 8 %.
г)
Для оценки силы связи признаков у
и х
найдем средний коэффициент эластичности:
![]() ,
где
,
где
![]() ,
,
![]()
Таким образом, в среднем на 0,48% по совокупности изменится среднедневная зарплата от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного на 1%.
д) Рассчитаем фактическое значение F – критерия при заданном уровне значимости = 0,05
 .
.
Сравнивая табличное
Fтабл=4,96
(см. лабораторная работа №1) и фактическое
![]() значения, отмечаем, что
значения, отмечаем, что
![]() ,
это указывает на необходимость отвергнуть
гипотезу Но
о статистически незначимых параметрах
уравнения показательной парной регрессии.
,
это указывает на необходимость отвергнуть
гипотезу Но
о статистически незначимых параметрах
уравнения показательной парной регрессии.
ж)
По условию задачи прогнозное значение
фактора выше его среднего уровня
![]() на 5%, тогда оно составляет:
на 5%, тогда оно составляет:
![]() ,
,
и прогнозное значение зарплаты при этом составит:
![]() руб.
руб.
Найдем ошибку прогноза:

Предельная ошибка
прогноза, которая в 95% случаев не будет
превышена, составит:
![]() .
.
Доверительный интервал прогноза при уровне значимости = 0,05:
(129,4589; 187,9211).
2. Проверим полученные результаты с помощью ППП MS Excel.
Результаты вычисления параметров показательной парной регрессии можно проверить с помощью ППП Excel, для чего используем встроенную статистическую функцию ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН (см. лабораторную работу №1 ).
В результате применения функции ЛГРФПРИБЛ дополнительная регрессионная статистика будет выводиться в порядке, указанном выше (табл. 4 лабораторной работы №1), причем в первой строке таблицы (рис.11) функция ЛГРФПРИБЛ возвращает коэффициенты показательной модели, остальные параметры соответствуют линеаризованной модели (рис.11).
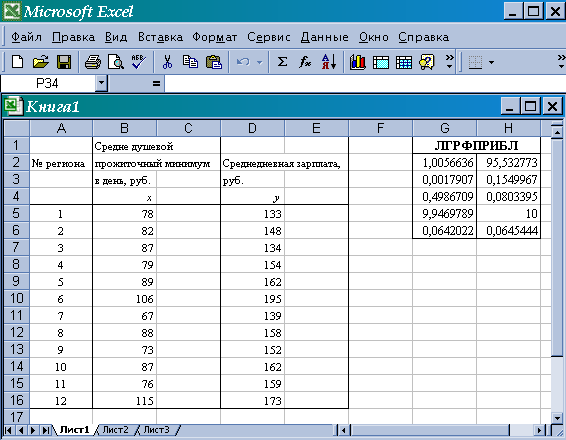
Рис. 11. Результат вычисления функции ЛГРФПРИБЛ
Прогнозное значение результата определим следующим образом:
активизируйте Мастер функций ,
в окне Категория (рис. 12) выберите Статистические, в окне Функция – РОСТ (рис. 3);

Рис.12. Диалоговое окно «Мастер функций»

Рис.13. Диалоговое окно ввода аргументов функции РОСТ
3) заполните аргументы функции (рис.13)
Изв знач у – диапазон, содержащий данные результативного признака;
Изв знач х – диапазон, содержащий данные факторов независимого признака;
Нов _ знач _ х – новые значения х, для которых возвращается соответствующие значения у;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается свободным образом, если Константа = 0, то свободный член равен 0;
В данном случае прогнозируемое значение получилось равным 158,69. Сравнивая полученные вручную и с помощью ППП MS Excel. данные, убеждаемся в правильности выполненных действий.
Варианты заданий лабораторной работы №2
По территориям региона приводятся данные за 199Х год (табл.8).
Таблица 8
№ региона |
Среднедушевой прожиточный минимум в день , руб.,x |
Среднедневная заработная плата, руб., y |
1 |
70+2i |
133 |
2 |
90-4j |
148 |
3 |
80+i |
134 |
4 |
90-3i |
154 |
5 |
90+i |
162 |
6 |
110-5i |
195 |
7 |
60+j |
139 |
8 |
90-2j |
158 |
9 |
80-j |
152 |
10 |
87+0,5i |
162 |
11 |
75-0,1j |
159 |
12 |
110+0,1i |
173 |
где i, j две последние цифры номера зачетной книжки соответственно.
Требуется:
1. Для характеристики зависимости у от х:
а) построить показательное уравнение парной регрессии у от х;
б) оценить тесноту связи с помощью индексов корреляции и детерминации;
в) оценить качество показательного уравнения парной регрессии с помощью средней ошибки аппроксимации;
г) дать оценку силы связи с помощью среднего коэффициента эластичности;
д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера.
е) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости =0,05 .
2. Проверить полученные результаты с помощью ППП MS Excel.
Вопросы для самопроверки
В чем состоят ошибки спецификации модели?
Поясните смысл коэффициента регрессии, назовите способы его оценивания.
Что такое число степеней свободы и как оно определяется для факторной, остаточной, общей сумм квадратов?
Какова концепция F – критерия Фишера для показательной парной регрессии?
Каковы методы подбора вида математической функции .
Какова концепция дисперсионного анализа результатов регрессии?
Как находится интервальная оценка прогнозного значения по уравнению регрессии?
Запишите все виды моделей, нелинейных относительно:
- включаемых переменных;
- оцениваемых параметров.
В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров?
Как определяются коэффициенты эластичности ?
Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков.
В чем смысл средней ошибки аппроксимации и как она определяется?
Содержание отчета по лабораторной работе:
1) тема и цель лабораторной работы;
2) текст задания лабораторной работы;
3) результаты, зафиксированные на бумаге, в соответствии с изложенным выше выполнением типового задания лабораторной работы;
4) электронный вариант выполнения лабораторной работы;
5) защита лабораторной работы.
