Старательный И. И., УиА, 1-2,10.09.2012

Тема 1. Основы концепций представления детерминированной физической картины мира Лабораторная работа № 1

Использование компьютерного моделирования для представления пространства и детерминированных форм движения частиц

(Шрифт, Arial, 10)

Эксперимент 1. Изучение основных понятий, связанных с отражением объектов детерминистского физического мира в наших мыслительных образах в виде материальной точки (частицы), пространства и движения.

(Шрифт, Arial, 12)

Для характеристики местоположения частицы в пространстве и описания ее движения часто используют три способа:

1. Координатный.

2. Векторный.

3. Траекторный (естественный).

1.1 Координатный.

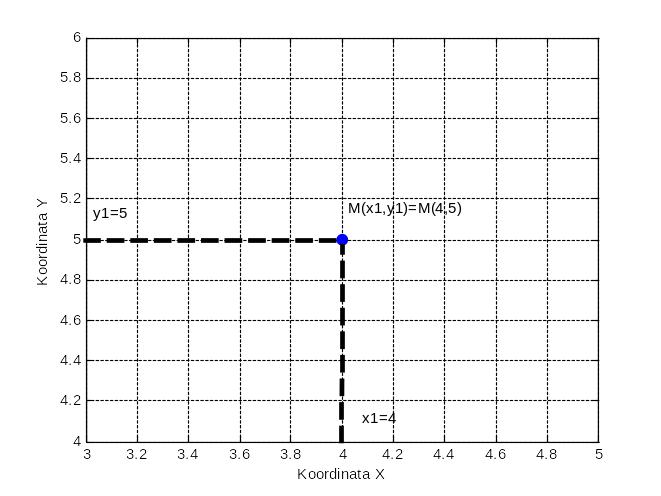
x1 = 4 y1 = 5

Вывод: при координатном способе местоположение частицы (точки) М(x1;y1) в двумерном пространстве (на плоскости) характеризуют парой чисел (x1;y1), то есть ее прямоугольными координатами.

1.2. Изменение местоположения при координатном способе

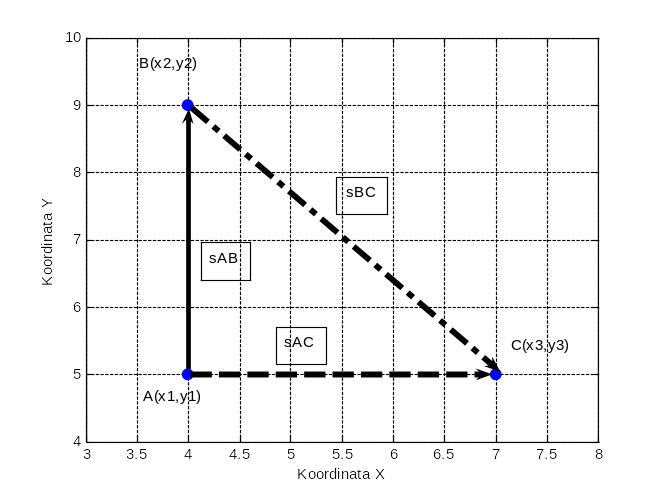
Вывод: в случае, если движение частицы осуществляется по линии, параллельной одной из осей координат, то при координатном способе изменение местоположения частицы (точки) М(x1;y1) в двумерном пространстве определяется разностью прямоугольных координат, соответствующих началу и концу движения (sAB =4 [9-5]), sAC=3 [7-4]). В случае, если движение осуществляется по прямой, наклонной к осям, то пройденный путь оценивают, пользуясь теоремой Пифагора (sBC = 5).

1.3 Векторный

Proek_xa = 3 Proek_ya = 4

1.4 Векторное описание движения

Вывод: при использовании векторного способа описания движения частицы при перемещении в пространстве частицы М меняются модуль и направление радиус – вектора . Геометрическое место точек пространства, где частица М побывала за время своего движения, называется ее траекторией. При векторном способе описания траекторией будет кривая, описываемая концом радиус вектора во все моменты времени ее движения (годограф векторной функции).

5. Траекторный

Вывод: при использовании траекторного способа описания движения частицы перемещение в пространстве частицы М характеризуют траекторией. Траектория L частицы представляет собой множество всех точек плоскости, координаты которых удовлетворяют уравнению . Траектория описывается (в заданной системе координат) уравнением кривой L . Этому уравнению удовлетворяют координаты х и у любой точки, лежащей на кривой L и не удовлетворяют координаты никакой другой точки не лежащей на этой кривой.

6. Траектория движения в виде эллипса и ее характеристики

7. Параметры эллипсоидов, характеризующих движение по Земле

WGS-84

Величина экваториальной полуоси эллипса a = 6378137

Величина полярной полуоси эллипса b = 6.3568e+006

Величина эксцентриситета эллипса exent = 0.0818

ПЗ-90

Величина экваториальной полуоси эллипса a = 6378136

Величина полярной полуоси эллипса b = 6.3568e+006

Величина эксцентриситета эллипса exent = 0.0818

Красовского

Величина экваториальной полуоси эллипса a = 6378245

Величина полярной полуоси эллипса b = 6.3569e+006

Величина эксцентриситета эллипса exent = 0.0818

Эксперимент 2. Изучение основных характеристик движения материальной точки (частицы) в пространстве

2.9. Вывод:

1. В случае, если мы имеем дело с прямолинейным равномерным поступательным движением вдоль одной координаты, то движение частицы происходит с постоянной скоростью (материальная точка за равные промежутки времени проходит одинаковые расстояния).

2. В случае, если при движении частицы вдоль одной координаты изменение скорости происходит не пропорционально времени и, соответственно, мы имеем дело с прямолинейным неравномерным поступательным движением вдоль одной координаты, то в этом случае скорость и ускорение являются функциями времени: .