
- •Рабочая программа дисциплины Математический анализ
- •1. Цели освоения дисциплины
- •2.Место дисциплины в структуре ооп бакалавриата
- •3. Компетенции обучающегося, формируемые в результате освоения дисциплины «Математический анализ»:
- •4. Структура и содержание дисциплины «Математический анализ»
- •5. Образовательные технологии
- •6. Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины.
- •Программа дисциплины «Математический анализ»
- •Объем дисциплины и виды учебной работы
- •Методические рекомендации для преподавателей дисциплины «Математический анализ»
- •Темы лекционных занятий
- •3 Семестр
- •Темы практических занятий
- •3 Семестр
- •Литература
- •Технологическая карта
- •2 Семестр
- •Система оценивания
- •Вопросы к экзамену
- •Типовые задания для контрольных и самостоятельных работ.
- •Примерные варианты контрольных работ Контрольная работа № 1
- •Контрольная работа № 2
- •Примерные тестовые задания по математическому анализу
- •7. Учебно-методическое и информационное обеспечение дисциплины «Теория вероятностей и математическая статистика»
- •8. Материально-техническое обеспечение дисциплины (модуля)
Контрольная работа № 2
Вариант № 1
Найти производные функции: а)
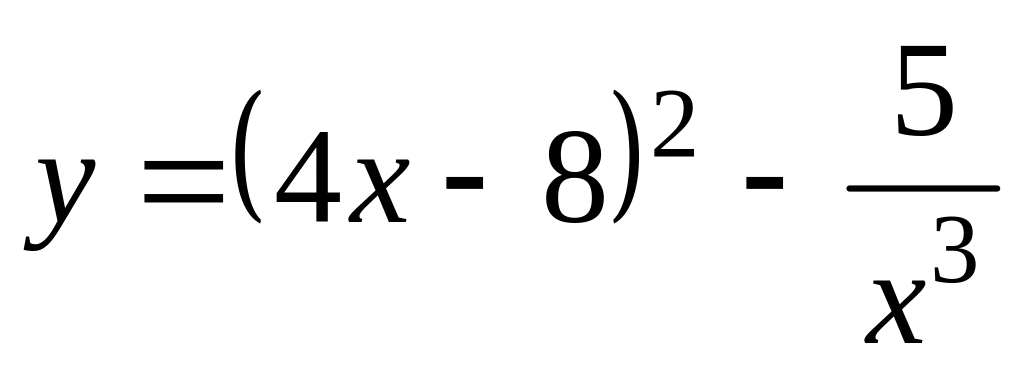 ;
б)
;
б)
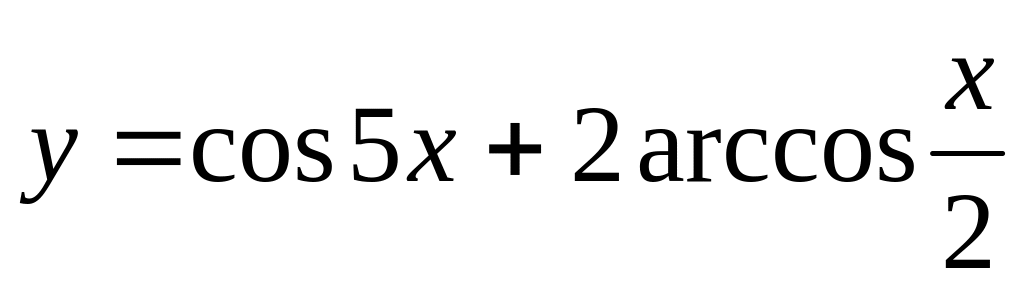 ;
в)
;
в)
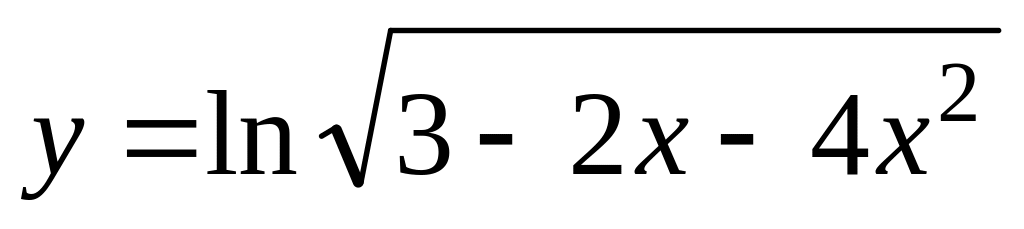
а)
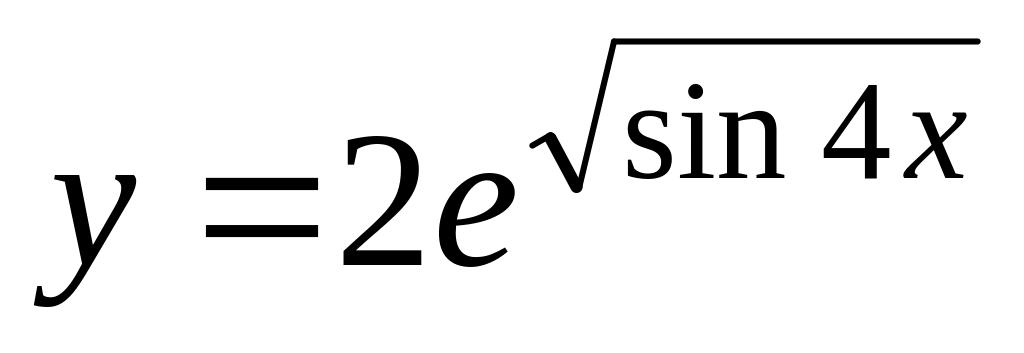 ;
б)
;
б)
 ;
в)
;
в)
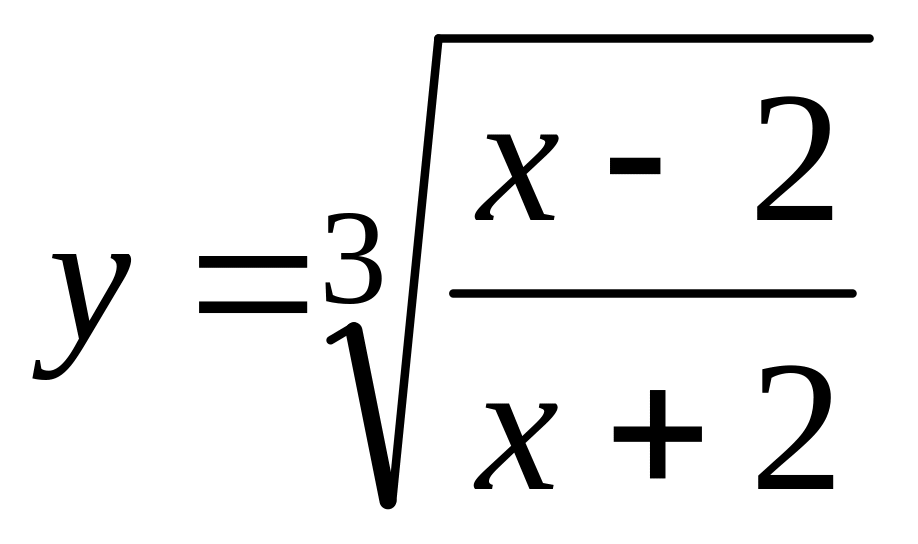
а)
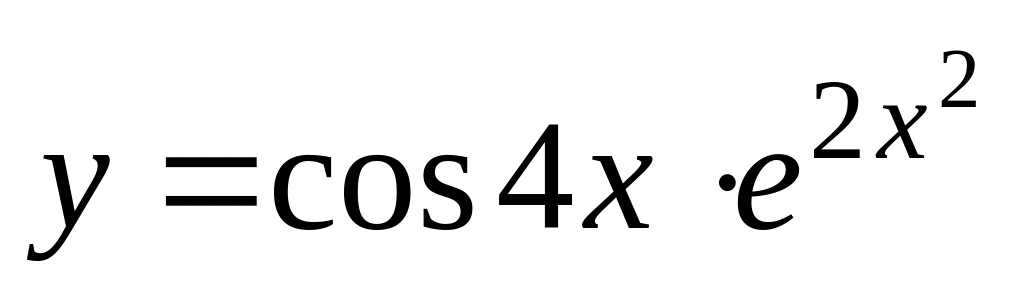 б)
б)
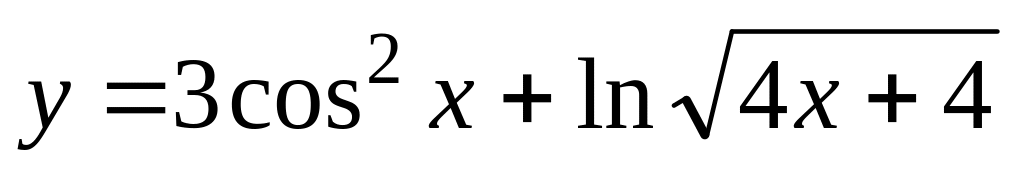 ;
в)
;
в)
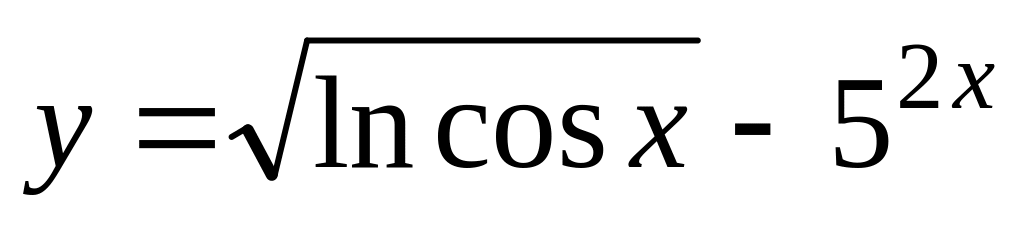 ;
г)
;
г)
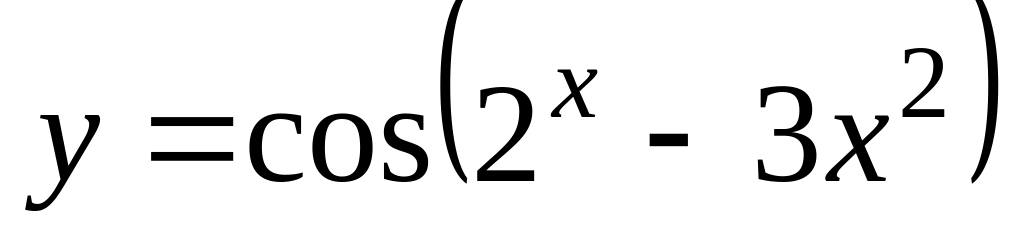
а)
 ;
б)
;
б)
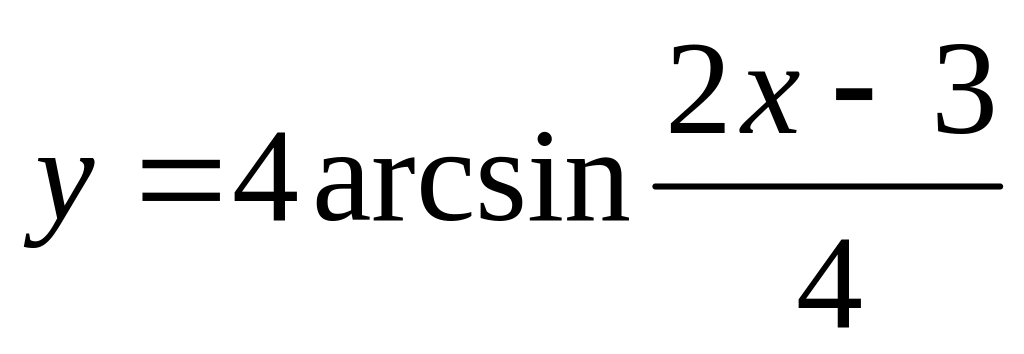 ;
в)
;
в)
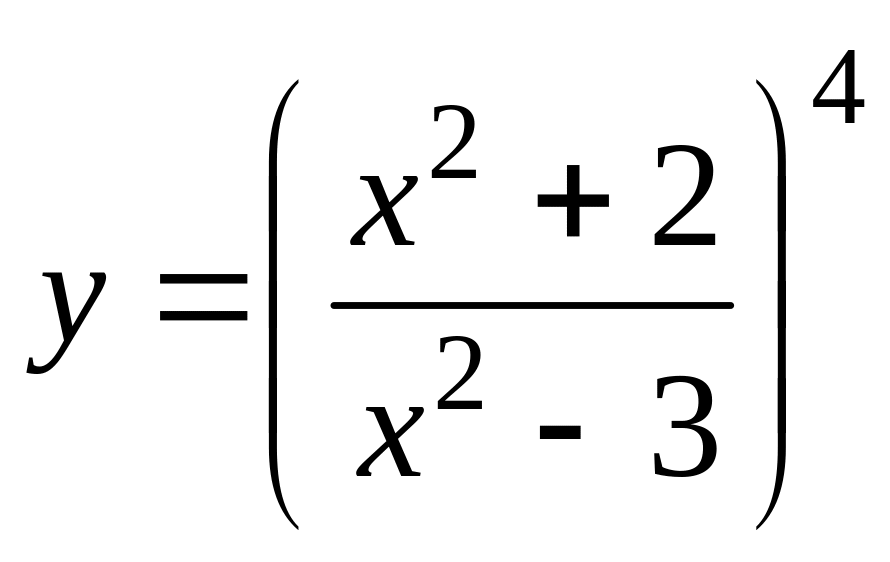 ;
г)
;
г)
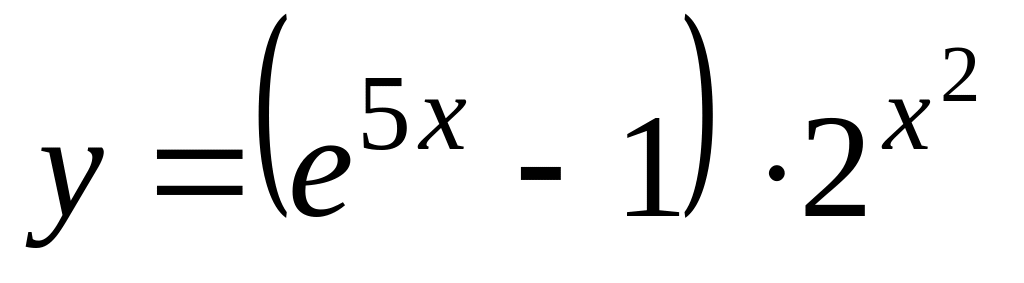
Найти пределы, используя правило Лопиталя:
а)
 ;
б)
;
б)
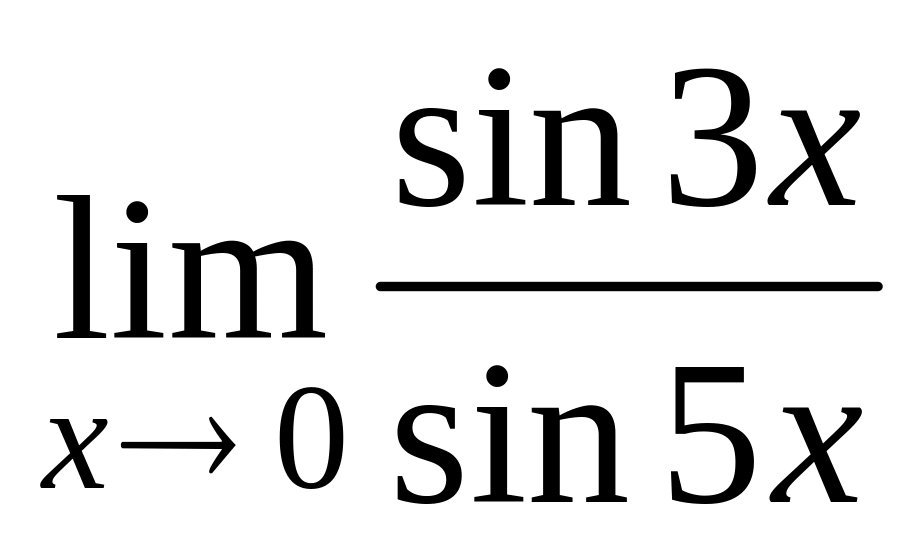 ;
в)
;
в)
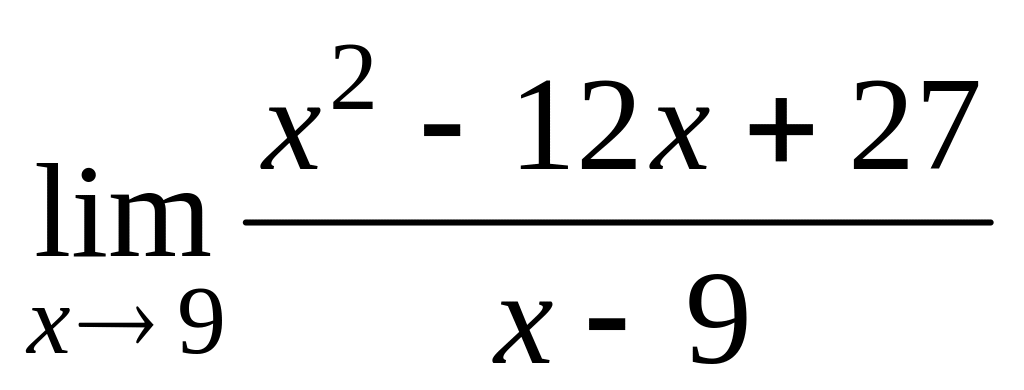 ;
г)
;
г)
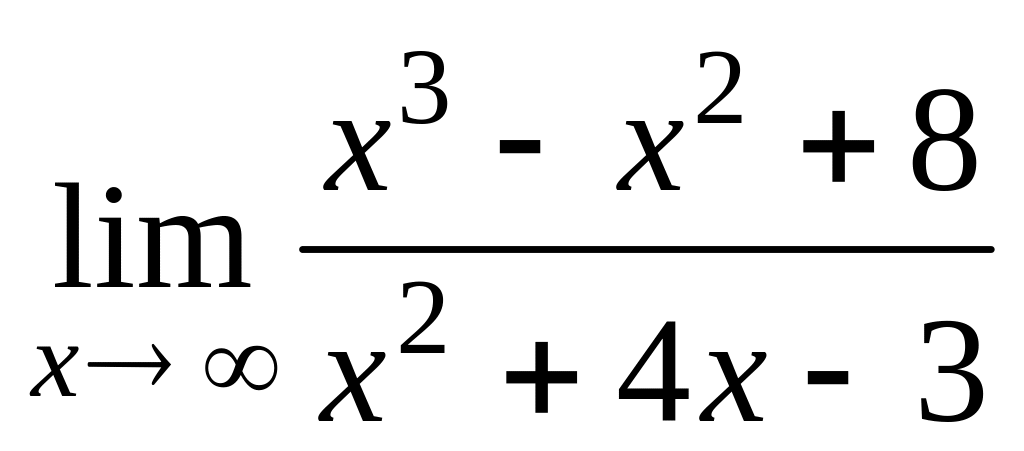 ;
д)
;
д)
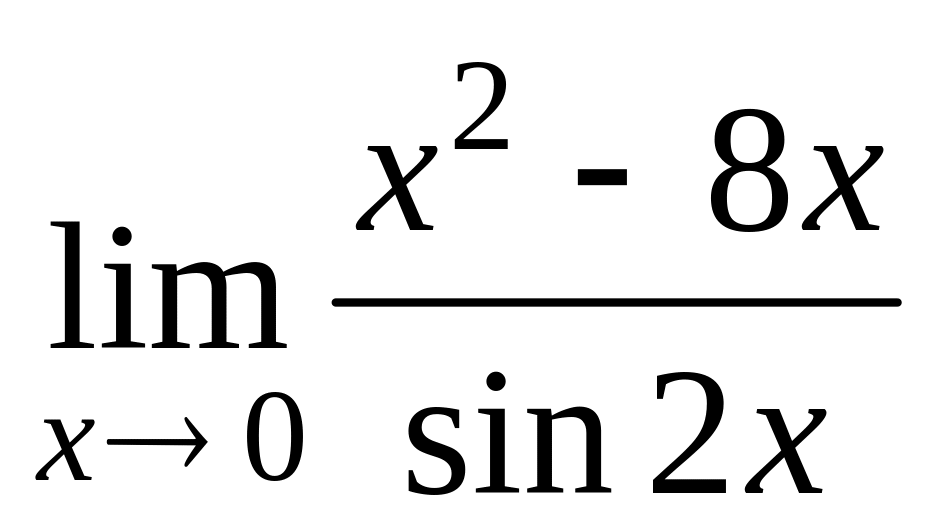
е)
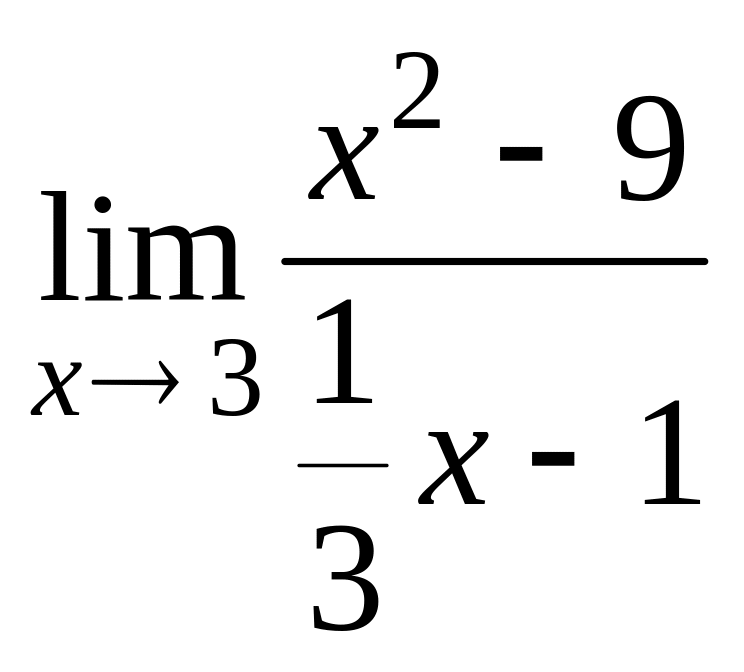 ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
Исследовать функцию и построить ее график: а) ;
Вариант № 2
Найти производные функции: а)
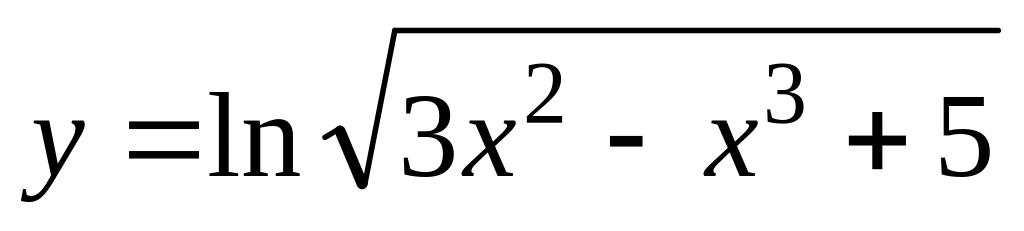 ;
б)
;
б)
 ;
в)
;
в)
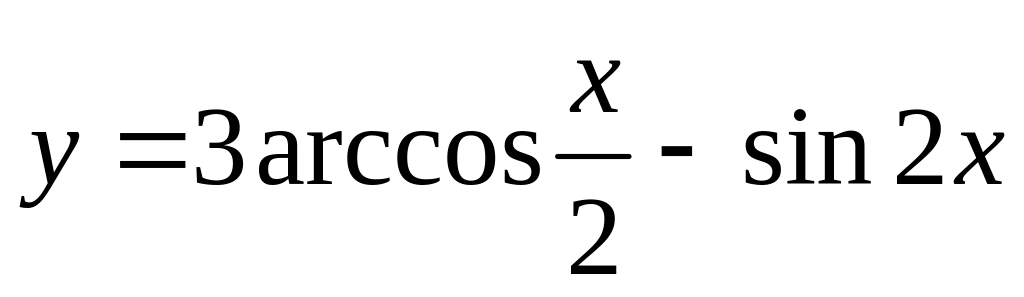
а)
 ;
б)
;
б)
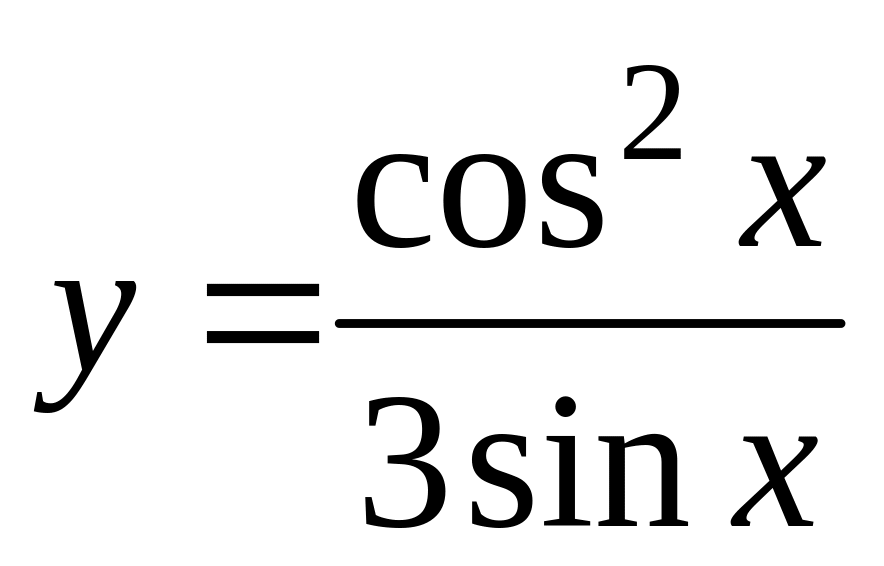 ;
в)
;
в)
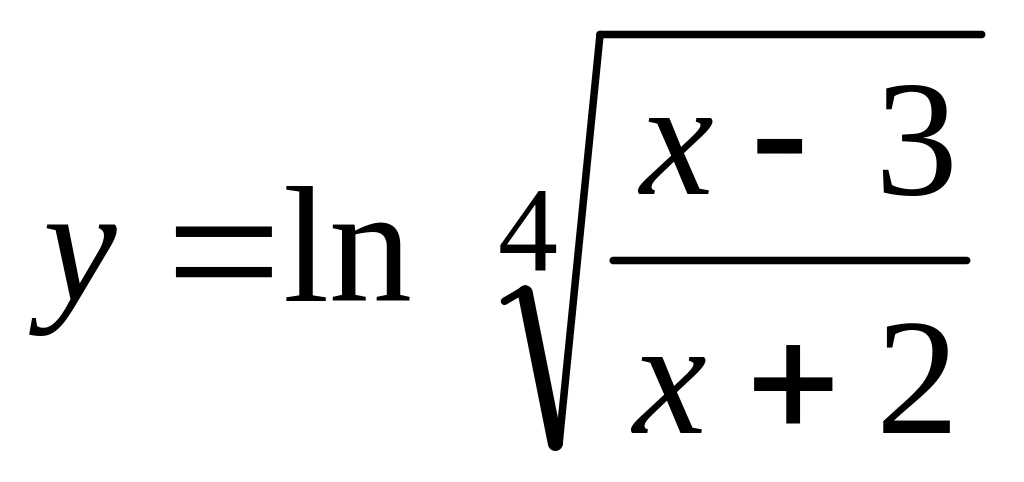
а)
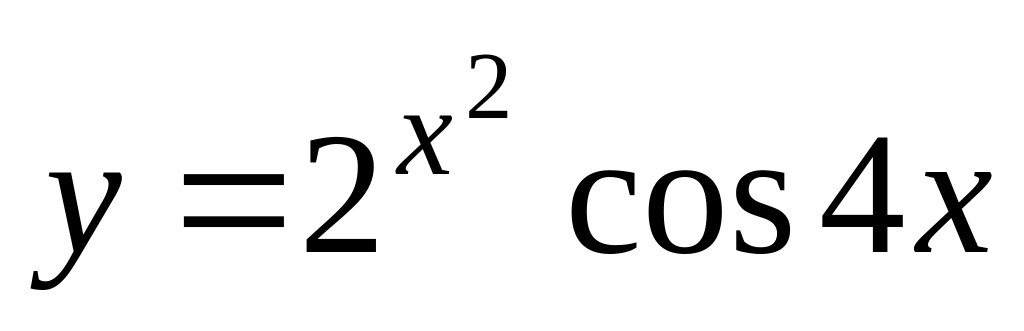 ;
б)
;
б)
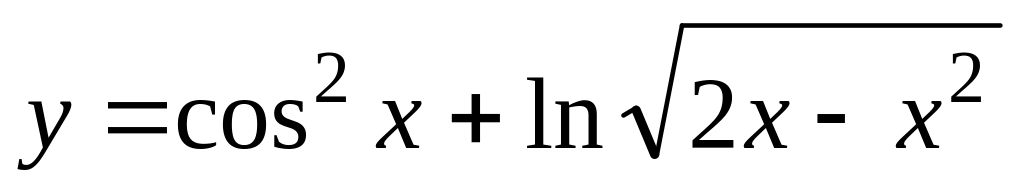 ;
в)
;
в)
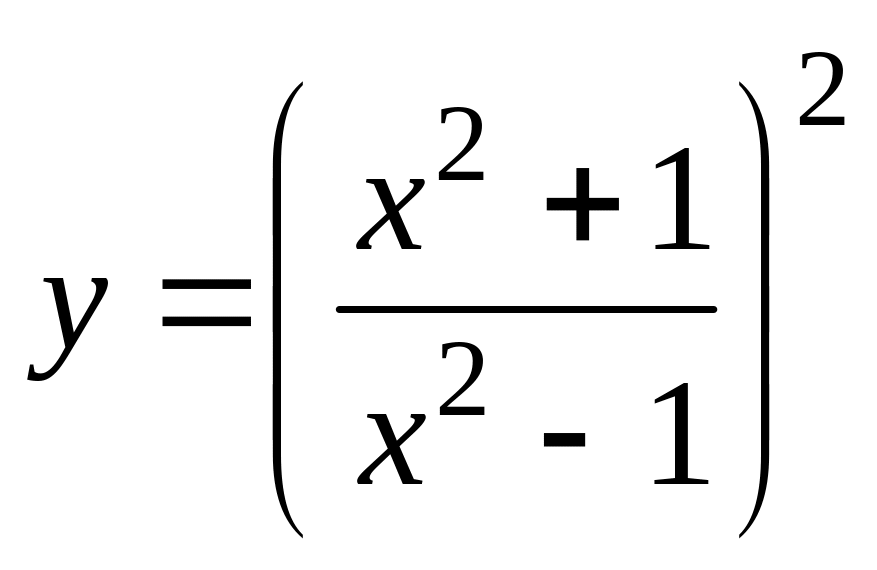 ;
г)
;
г)
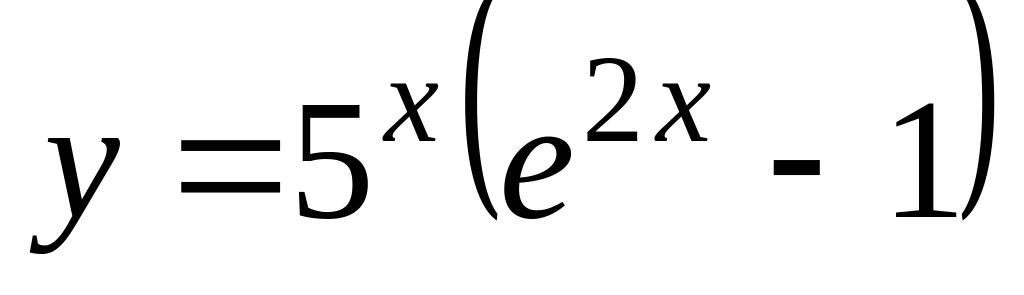
а)
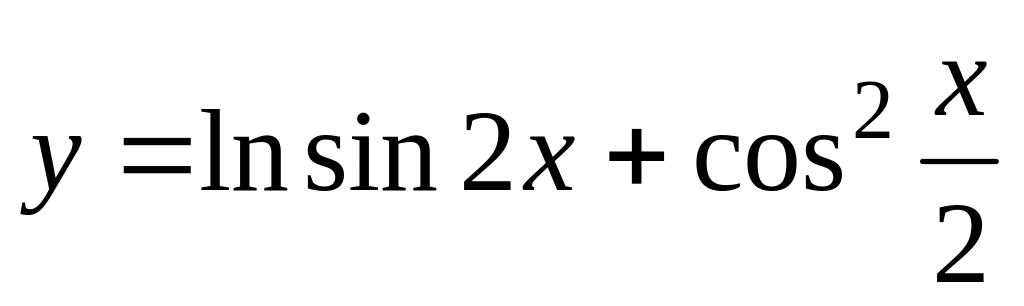 ;
б)
;
б)
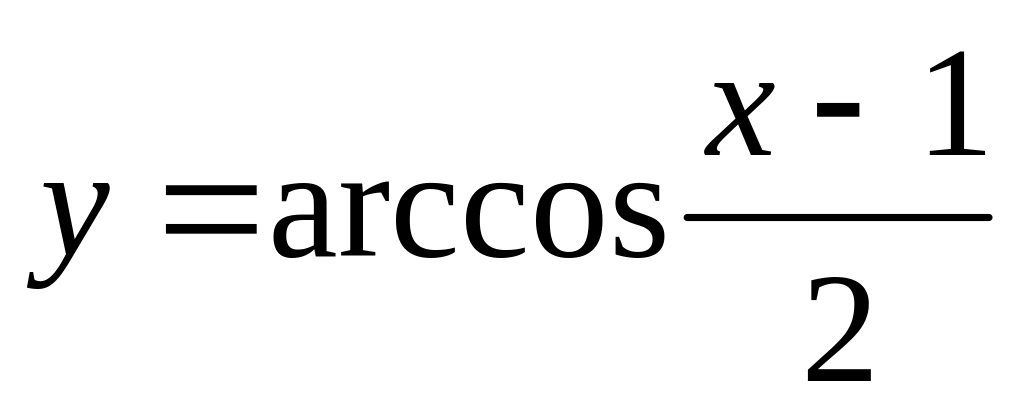 ;
в)
;
в)
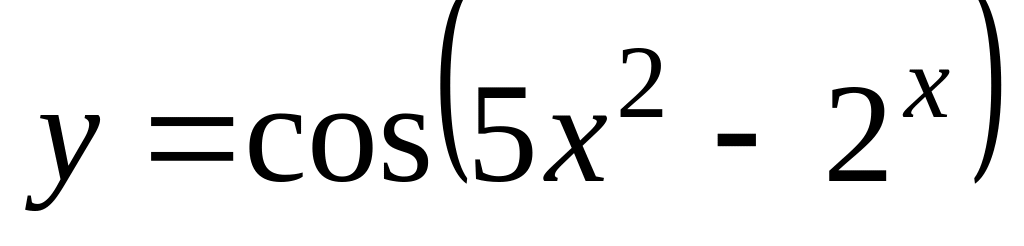 ;
г)
;
г)
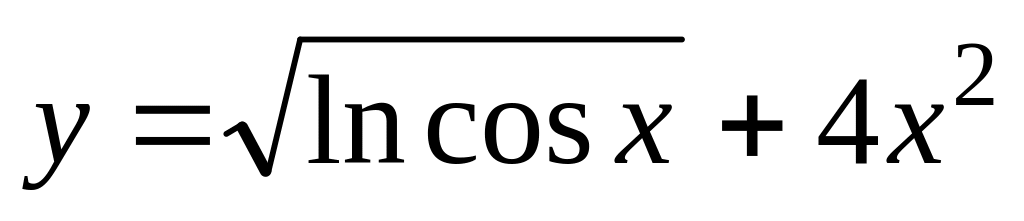
Найти пределы, используя правило Лопиталя:
а)
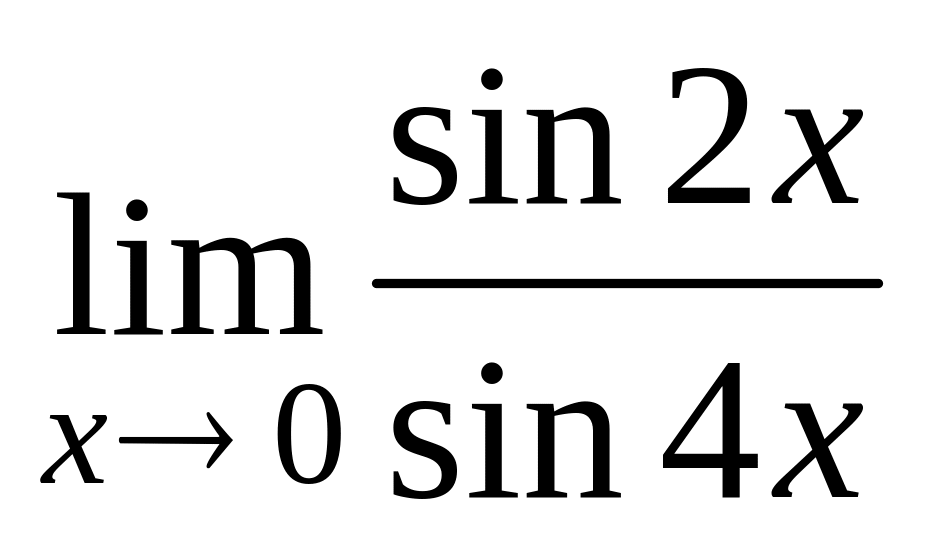 ;
б)
;
б)
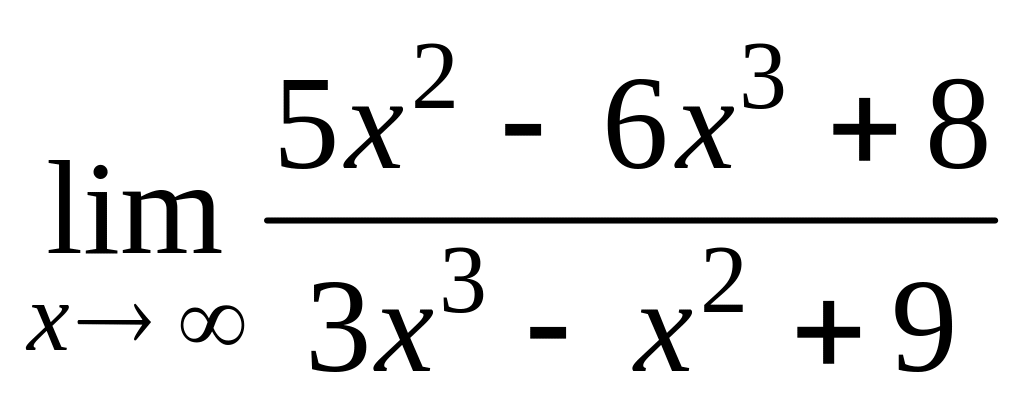 ;
в)
;
в)
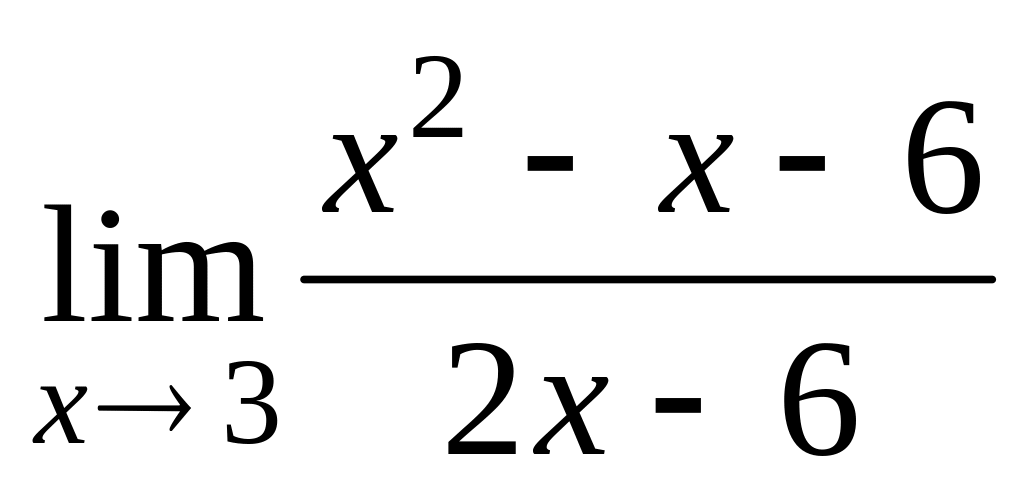 ;
г)
;
г)
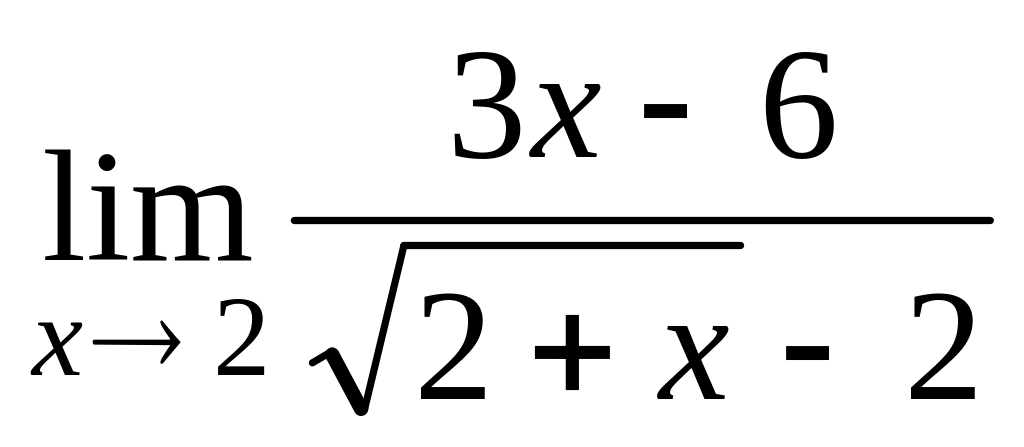 ;
д)
;
д)
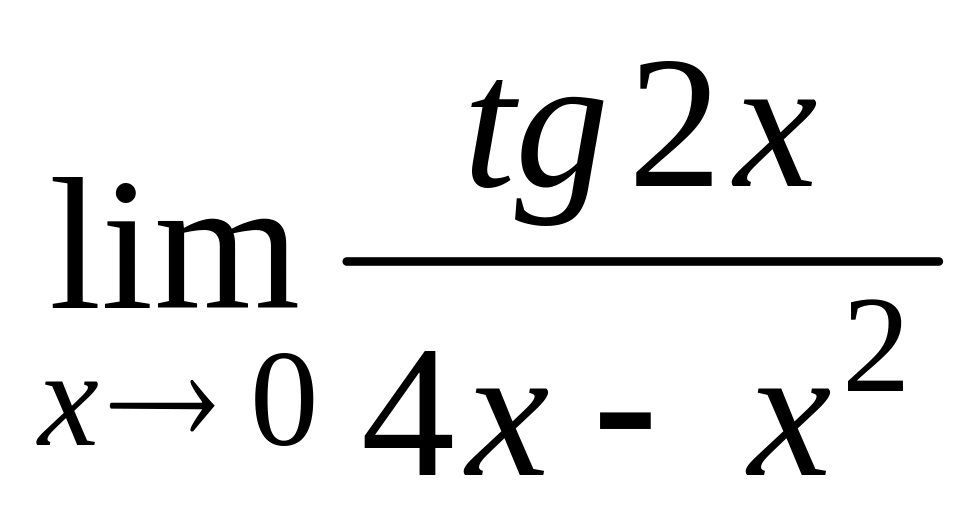 ;
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
Исследовать функцию и построить ее график: а) ;
Вариант № 3
Найти производные функции: а)
 ;
б)
;
б)
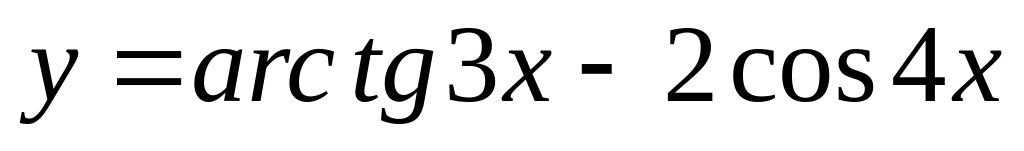 ;
в)
;
в)
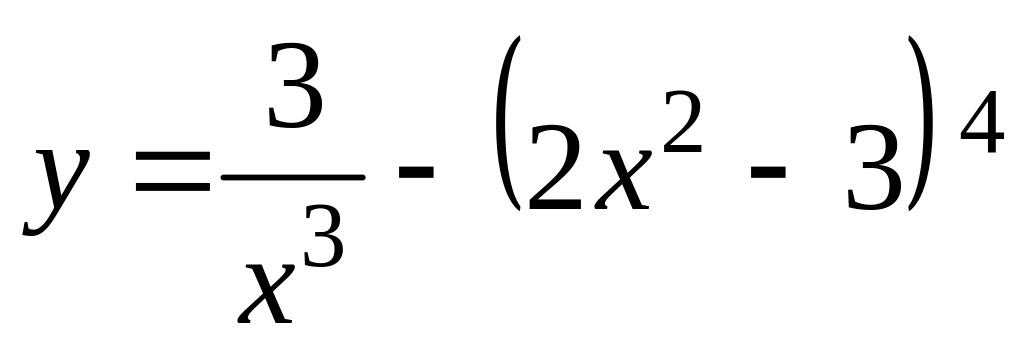
а)
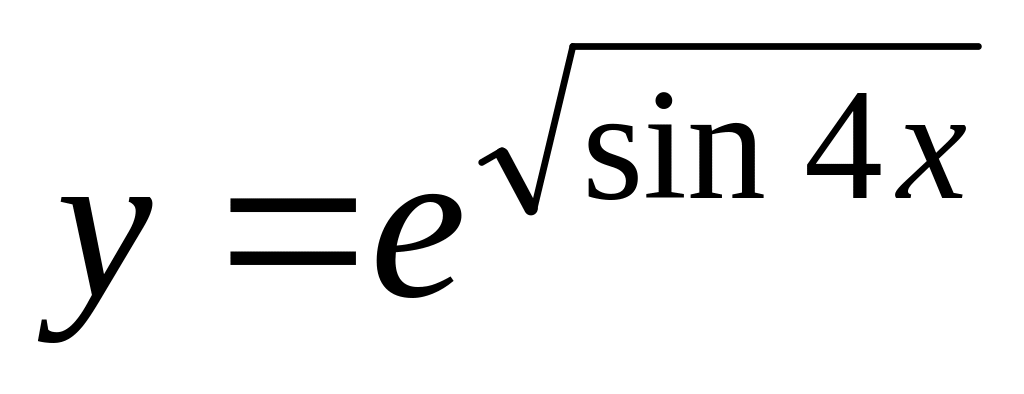 ;
б)
;
б)
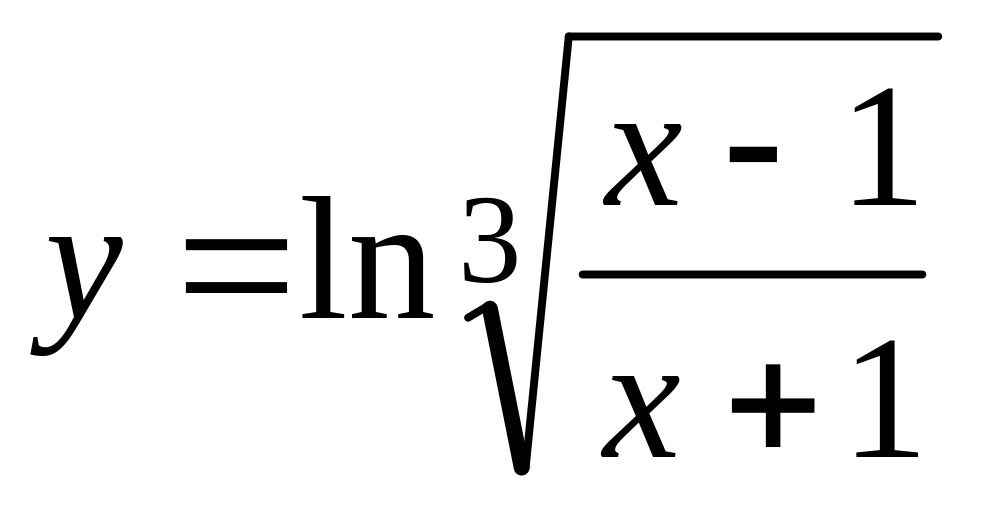 ;
в)
;
в)
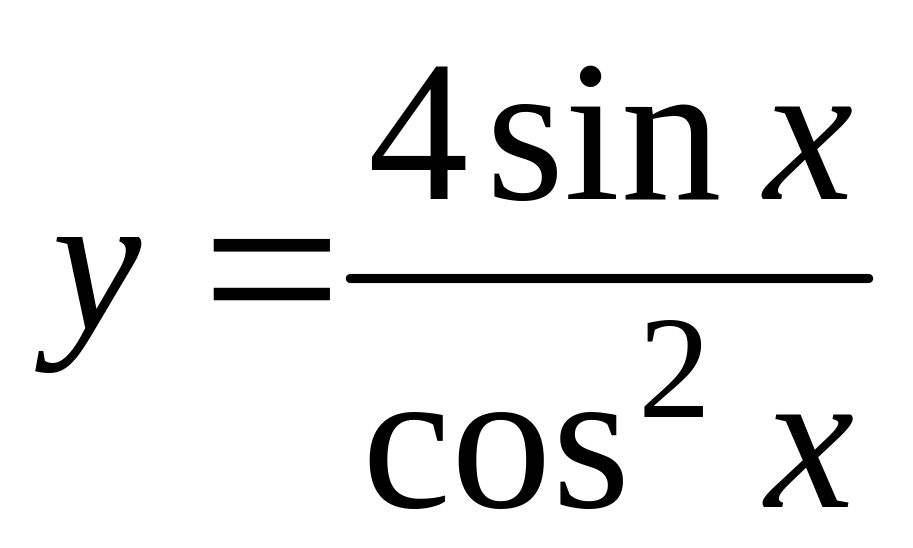
а)
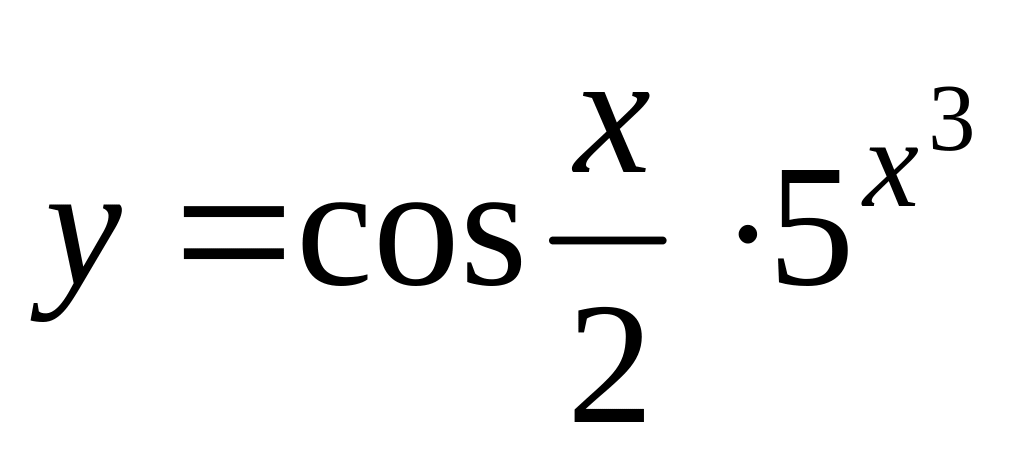 ;
б)
;
б)
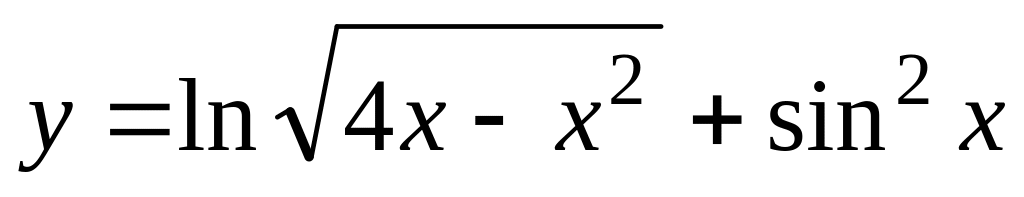 ;
в)
;
в)
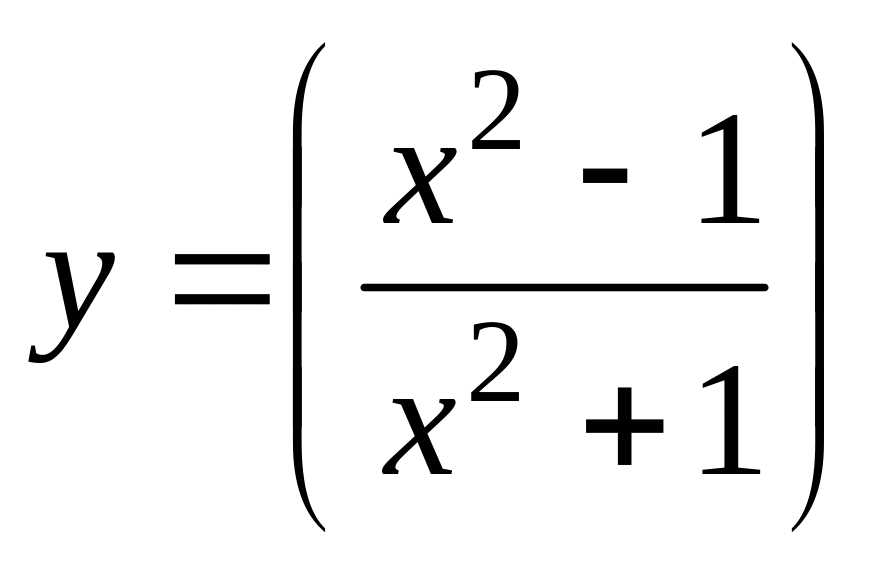 ;
г)
;
г)
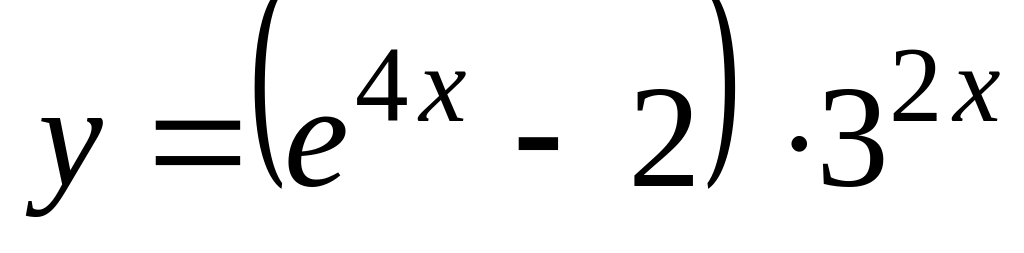
а)
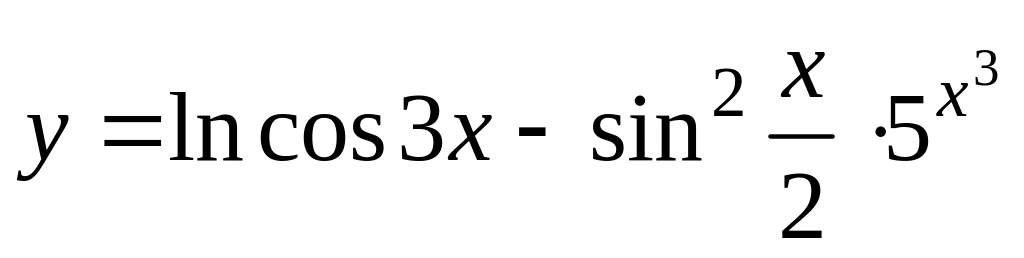 ;
б)
;
б)
 ;
в)
;
в)
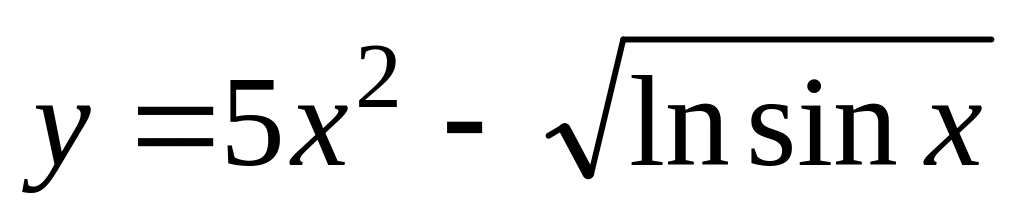 ;
г)
;
г)

Найти пределы, используя правило Лопиталя:
а) ; б)
 ;
в)
;
в)
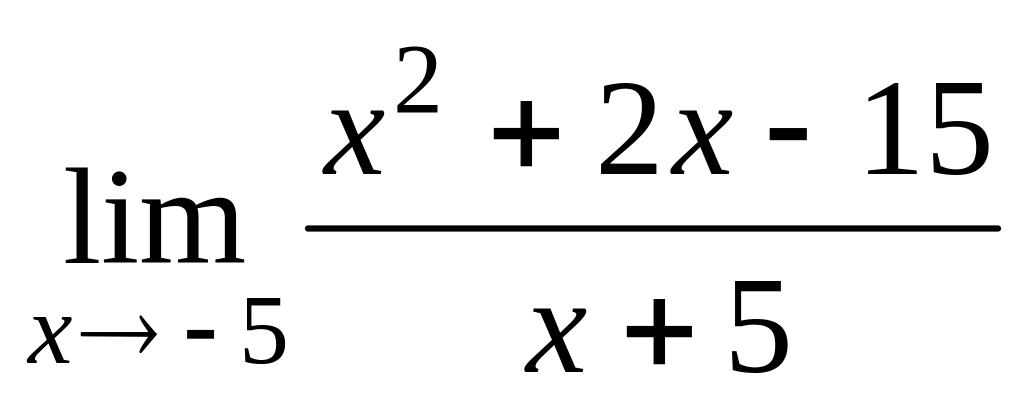 ;
г)
;
г)
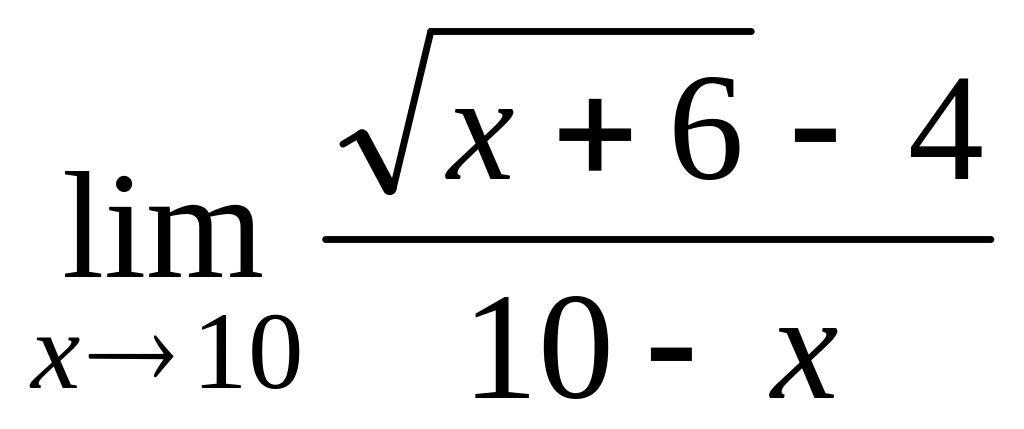 ;
д)
;
д)
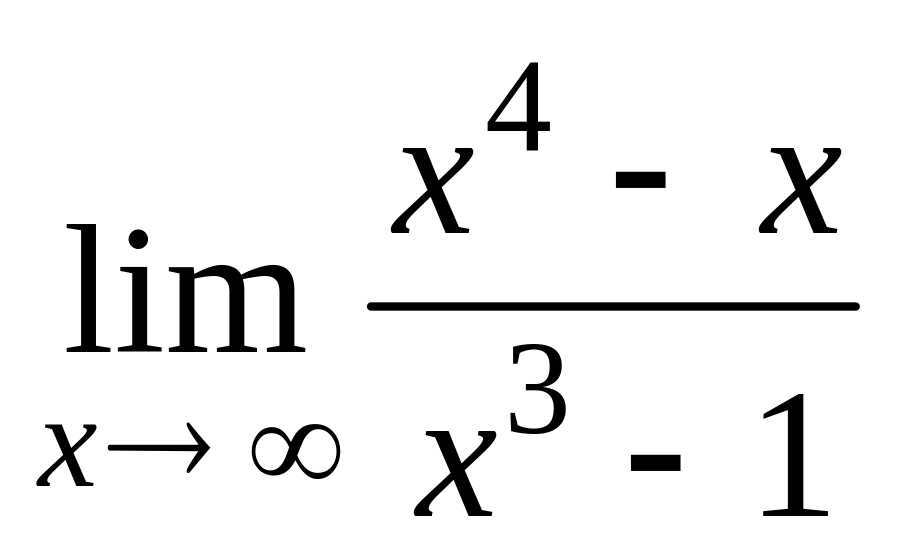
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
Исследовать функцию и построить ее график: а) ;
Вариант №4
Найти производные функции: а)
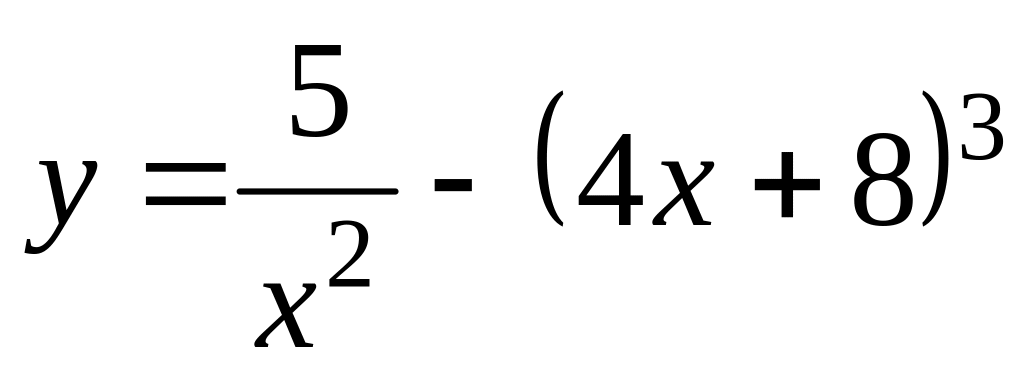 ;
б)
;
б)
 ;
в)
;
в)
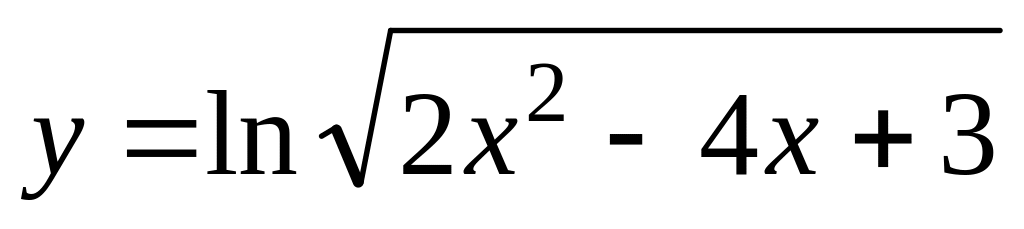
а)
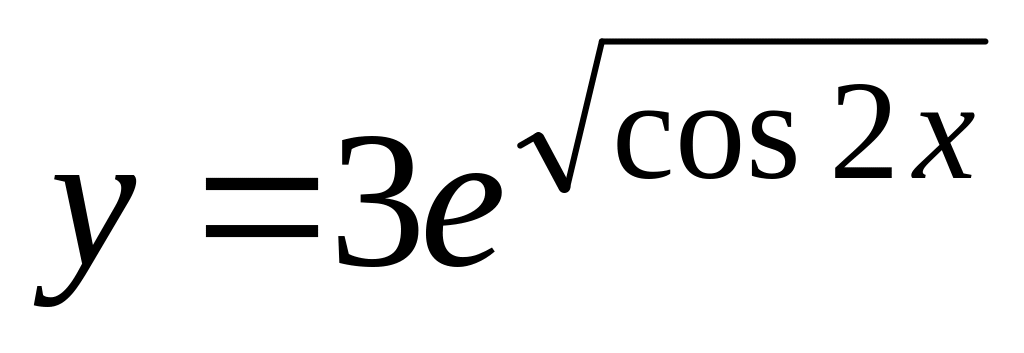 ;
б)
;
б)
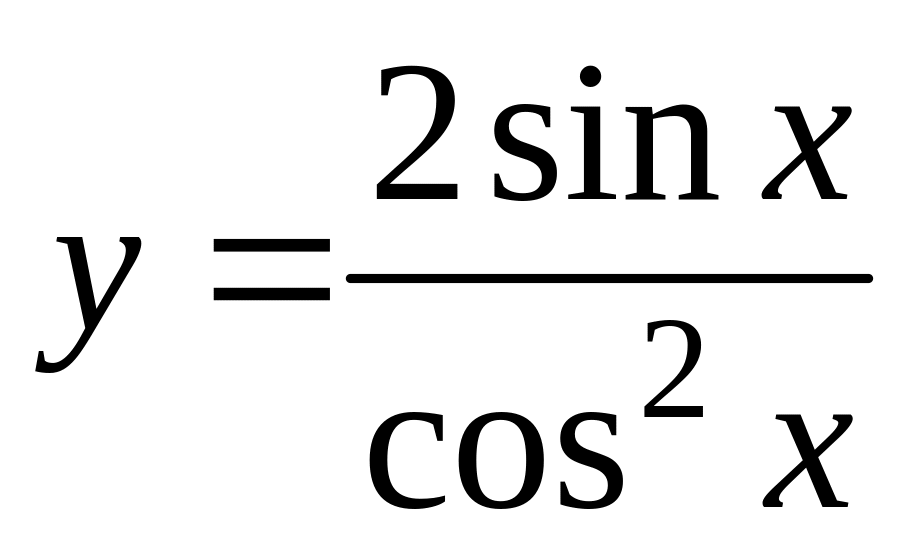 ;
в)
;
в)
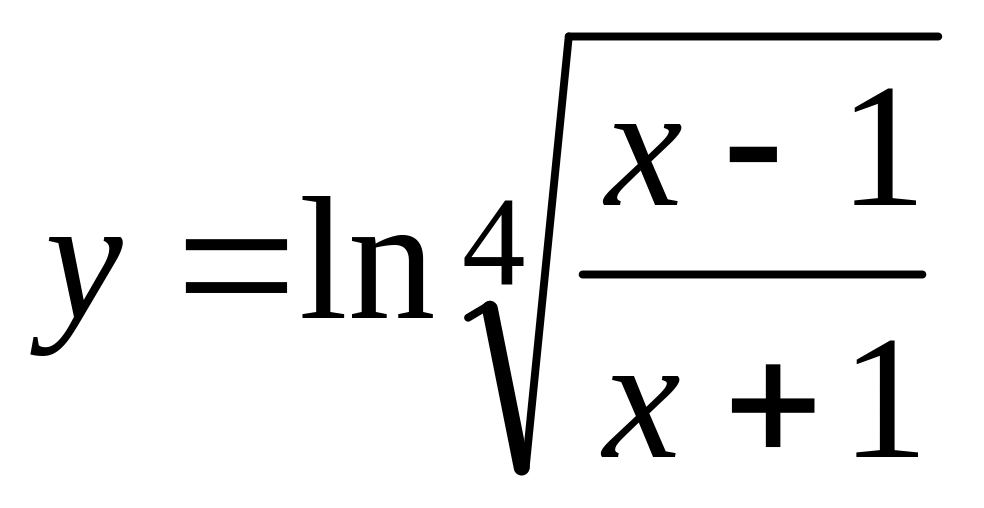
а)
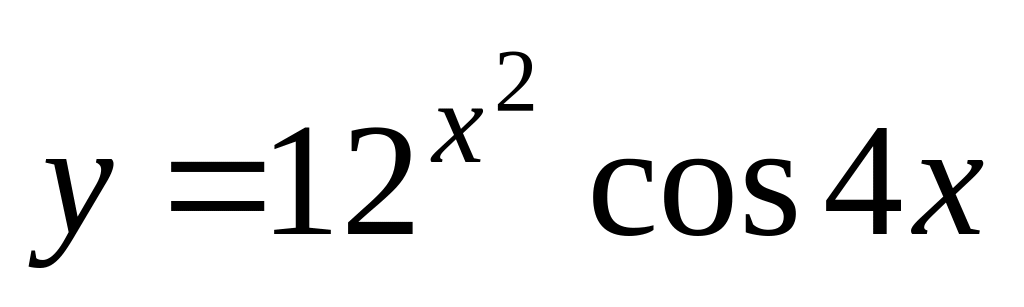 ;
б)
;
б)
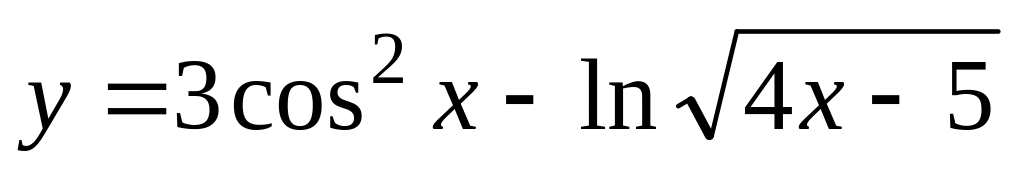 ;
в)
;
в)
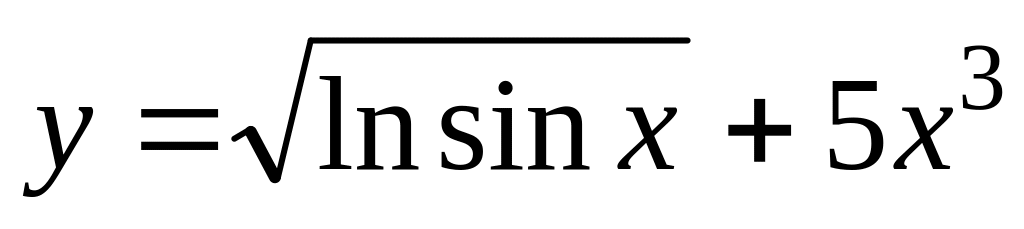 ;
г)
;
г)
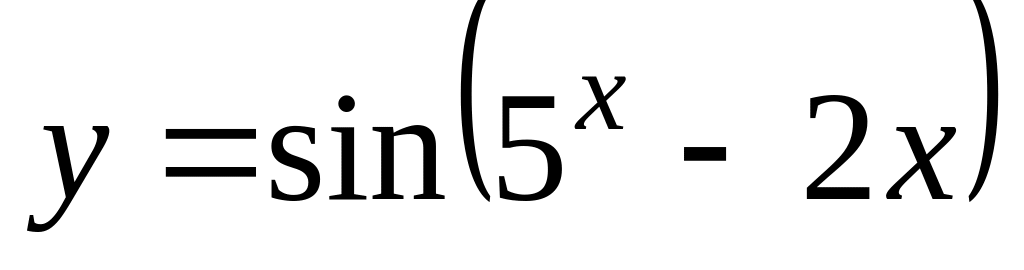
а)
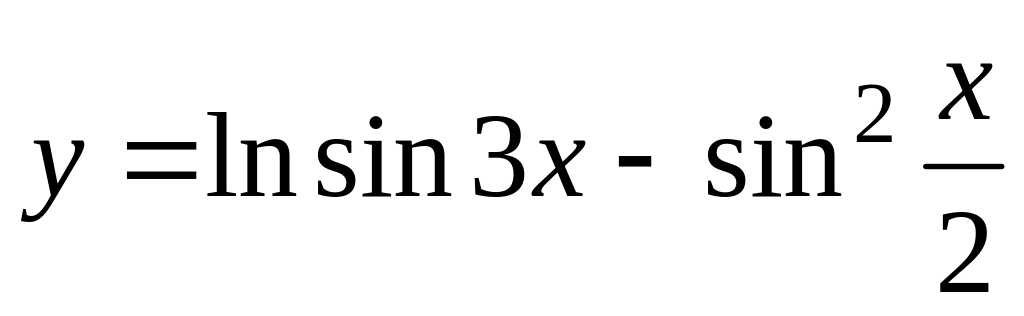 ;
б)
;
б)
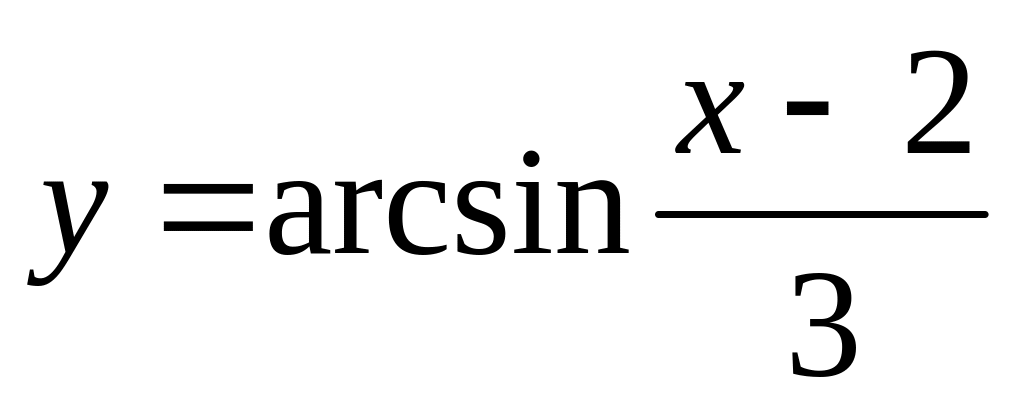 ;
в)
;
в)
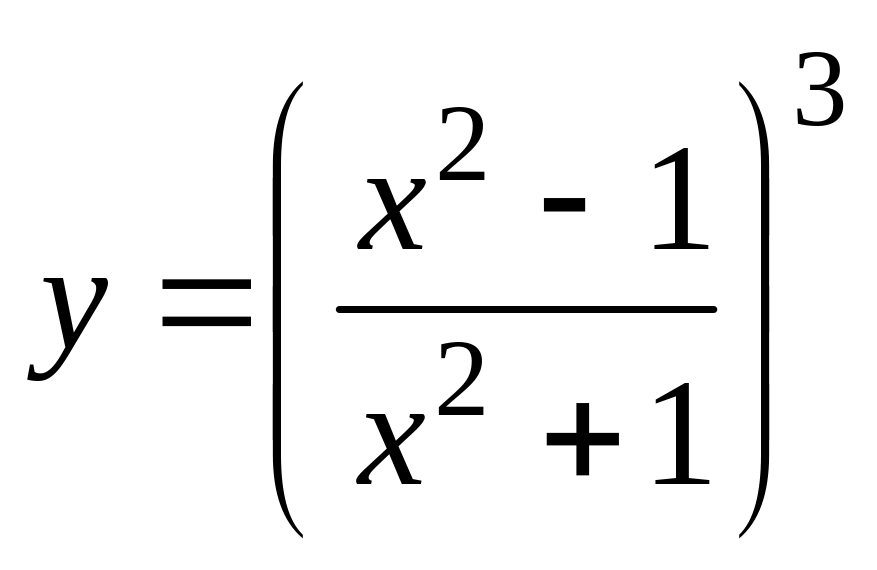 ;
г)
;
г)
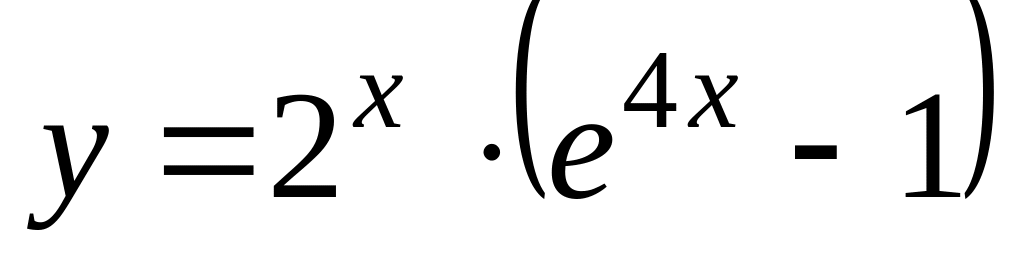
Найти пределы, используя правило Лопиталя:
а)
 ;
б)
;
б)
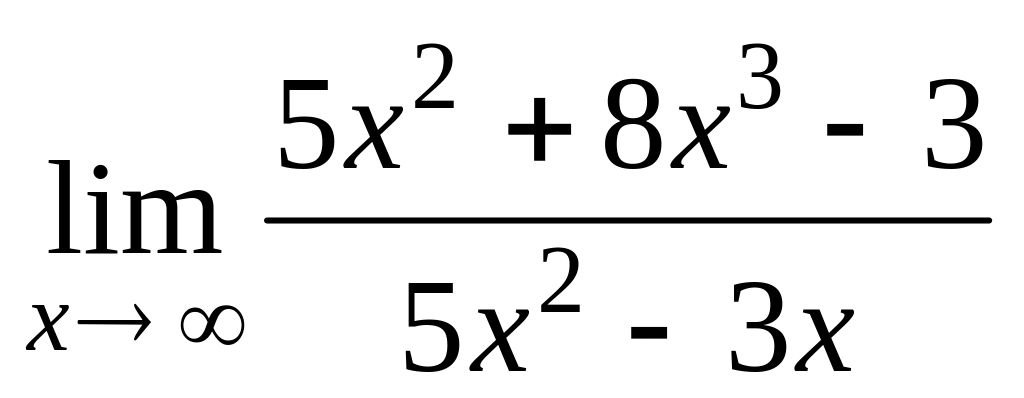 ;
в)
;
в)
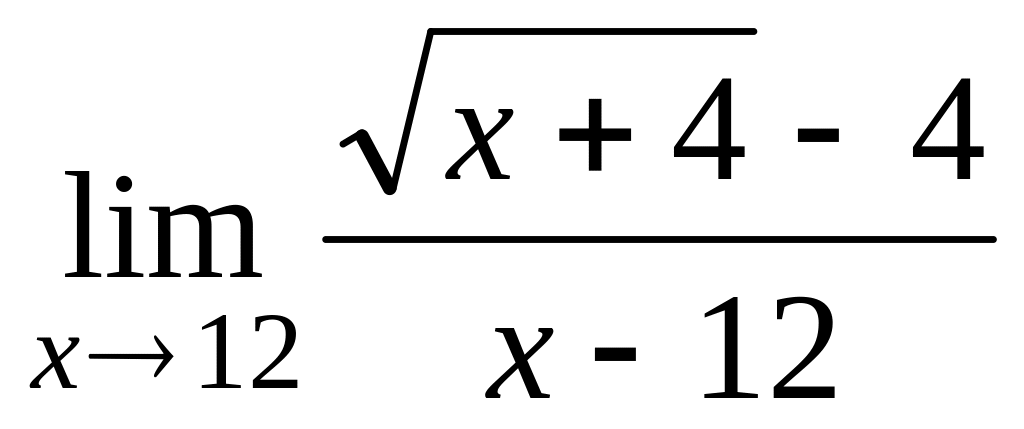 ;
г)
;
г)
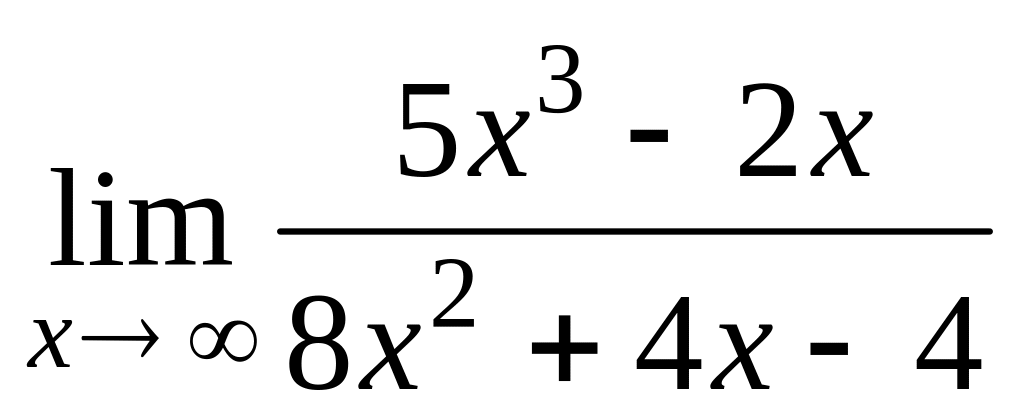 ;
д)
;
д)
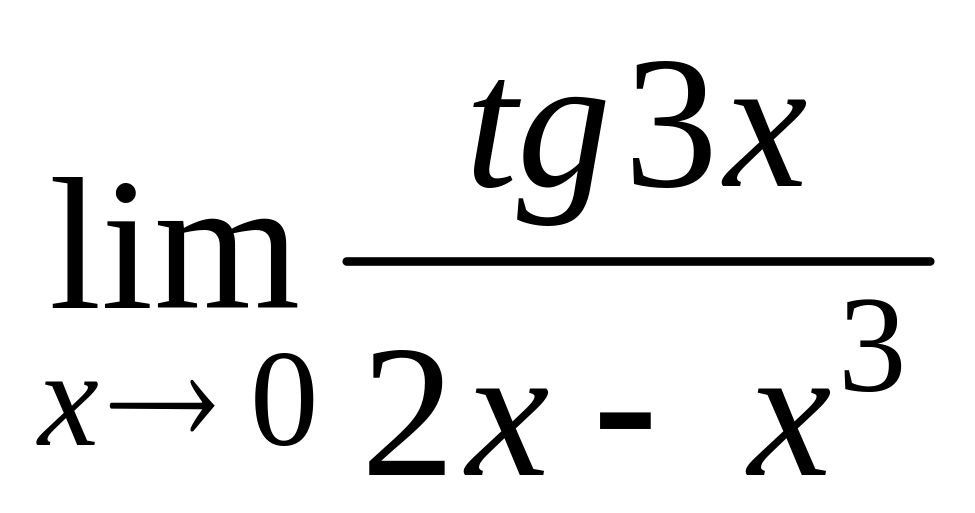 ;
;
е)
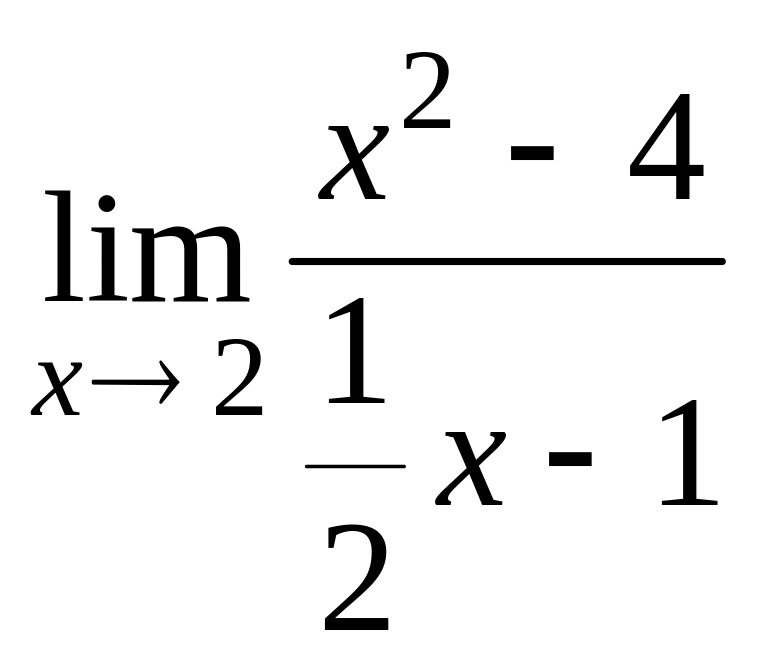 ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
Исследовать функцию и построить ее график: а) ;
Примерные тестовые задания по математическому анализу
Предел функции
![]() равен….
равен….
Ответ:
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4) 1
;
4) 1
2) Пределы функций
![]() и
и
![]() равны
равны
Ответ:
10 и
 ;
2)3 и 0,5; 3) -10 и 0,5; 4) 0 и 0,5
;
2)3 и 0,5; 3) -10 и 0,5; 4) 0 и 0,5
3) Производные функций
![]() и
и
![]() имеют вид…
имеют вид…
Ответ:
1)![]() и
и
![]() ;
2)
;
2)
![]() и -2tg x; 3)
и -2tg x; 3)
![]() и -2tg 4x;
4)
и 4tg 4x
и -2tg 4x;
4)
и 4tg 4x
4)Наименьшее и
наибольшее значение функции
![]() на отрезке
на отрезке
![]() равны…
равны…
Ответ:
1)-20 и 60; 2) 2 и 66; 3) -2 и 30; 4) 0 и 48
5) График функции
для на которой на всем отрезке
![]() одновременно выполняются условия
одновременно выполняются условия
![]() ,
,
![]() ,
,
![]() имеет вид…
имеет вид…
Ответ:
1
 )
2)
)
2)


3) 4)
20) Асимптотами
графика функции
![]() являются прямые …
являются прямые …
Ответ:
1)
![]() ,
y = 0; 2) x = 1,
y = x – 1; 3)
x = 1, y
= x; 4) x
= 1, y = x + 1
,
y = 0; 2) x = 1,
y = x – 1; 3)
x = 1, y
= x; 4) x
= 1, y = x + 1
6) Угловой коэффициент прямой проходящей через точки A(0;0); B(-1;4) равен…
Ответ:
-4; 2)
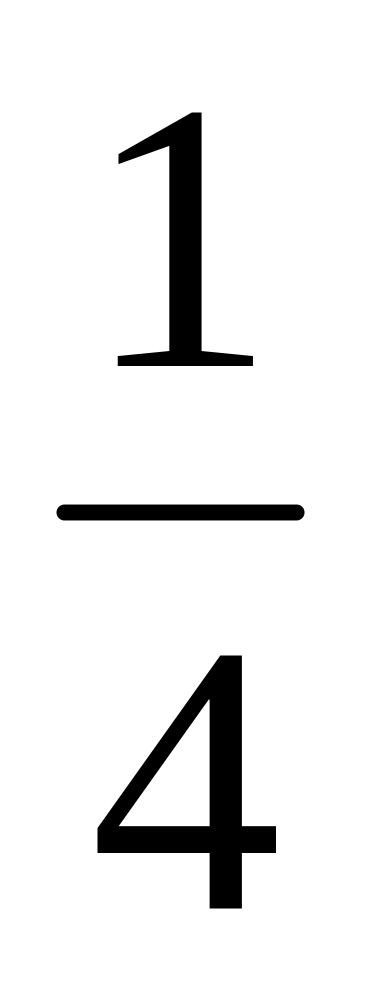 ;
3)
;
3)
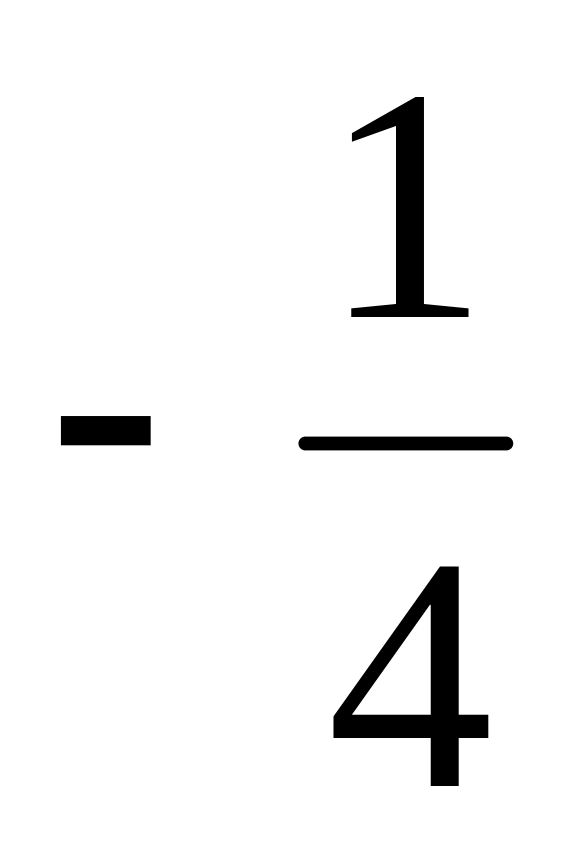 ;
4) 4
;
4) 4
22) Закон движения
материальной точки имеет вид x(t)![]() ,
где x(t) –
координаты точки в момент времени t.
Тогда скорость точки при t=7
равна ….
,
где x(t) –
координаты точки в момент времени t.
Тогда скорость точки при t=7
равна ….
Ответ: 1) 11; 2) 13; 3) 9; 4) 7,5
7) Общий член
последовательности
![]() имеет вид…
имеет вид…
Ответ:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
8) Суммы числовых рядов
![]() и
и
![]() соответственно равны…
соответственно равны…
Ответ:
2 и
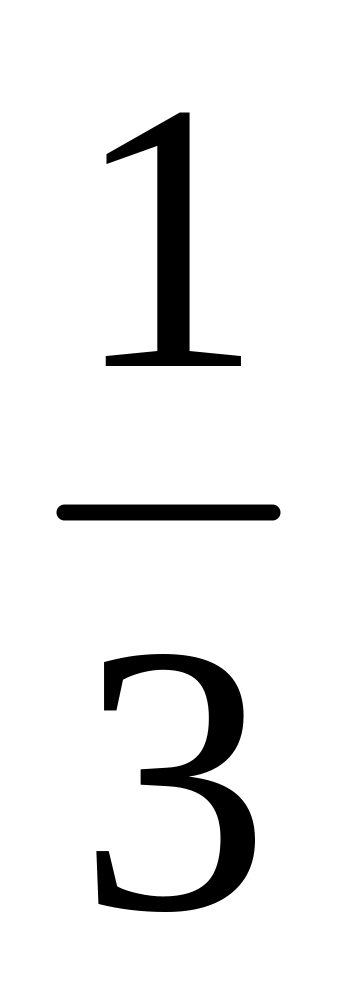 ;
2) 2 и 0,5; 3) 0,5 и 0,5; 4) 1 и
.
;
2) 2 и 0,5; 3) 0,5 и 0,5; 4) 1 и
.
9)Укажите правильное утверждение относительно сходимости числовых рядов
![]() и
и
![]()
Ответ:
1)А – расходится, В – сходится; 2) А и В расходится; 3) А и В – сходятся 4) А – сходится, В – расходится.
10)Если радиус
сходимости степенного ряда
![]() равен 5, то интервл его сходимости имеет
вид…
равен 5, то интервл его сходимости имеет
вид…
Ответ: 1) (-5;0); 2)
(0;5); 3) (-![]() ;5);
4) (-5;5).
;5);
4) (-5;5).
Коэффициент
 в разложении функции
в разложении функции
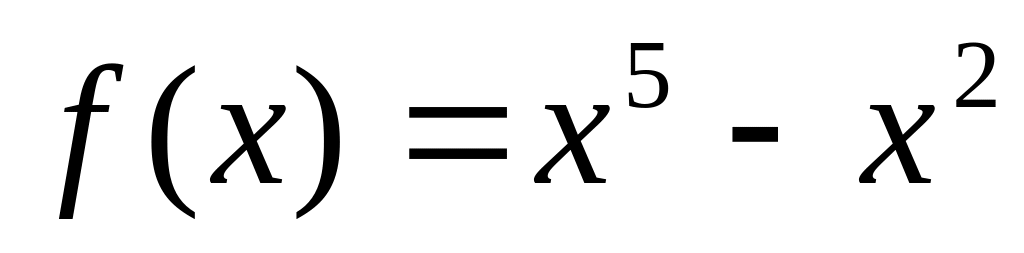 в ряд Тейлор по степеням (х-1) равен….
в ряд Тейлор по степеням (х-1) равен….
Ответ: 1) 3; 2) 12; 3) 1; 4) 24.
12) Неопределенные
интегралы
![]() и
и
![]() имеют вид …
имеют вид …
Ответ: 1) 2sin(2x+1)+c
и
![]() ;
2)
;
2)
![]() sin(2x+1)+c
и
sin(2x+1)+c
и
![]() ;
3) - 2sin(2x+1)+c
и
;
3) - 2sin(2x+1)+c
и
![]() ;
4)
;
4)
![]() sin(2x+1)+c
и
sin(2x+1)+c
и
![]()
Определенные интегралы
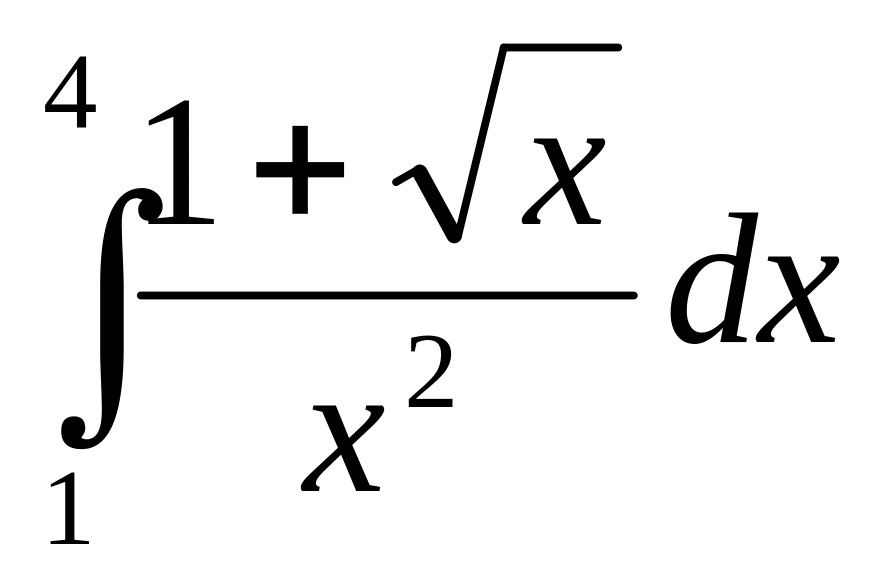 ;
;
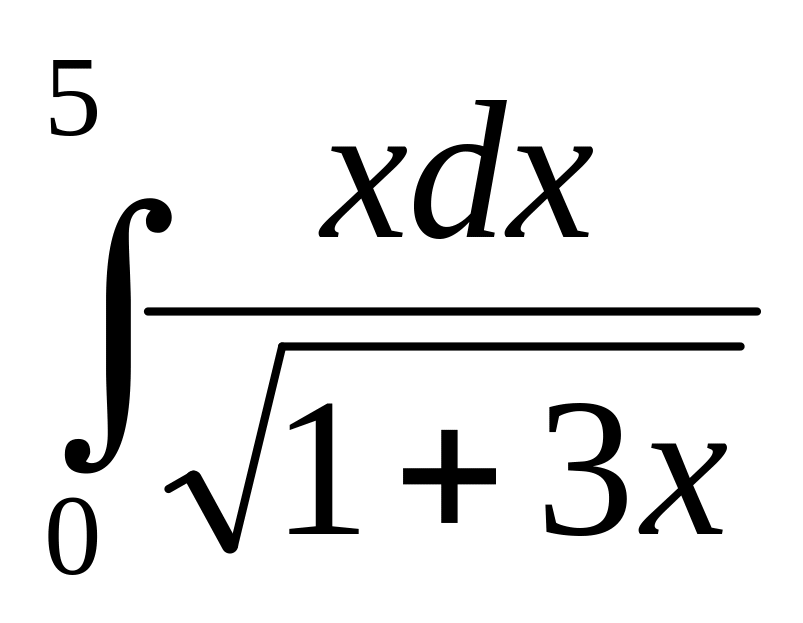 соответственно равны…
соответственно равны…
Ответ: 1)
![]() и 3; 2)
и 3; 2)
![]() и 14; 3)
и 14; 3)
![]() и 2; 4)
и 4.
и 2; 4)
и 4.
Частные производные от функции
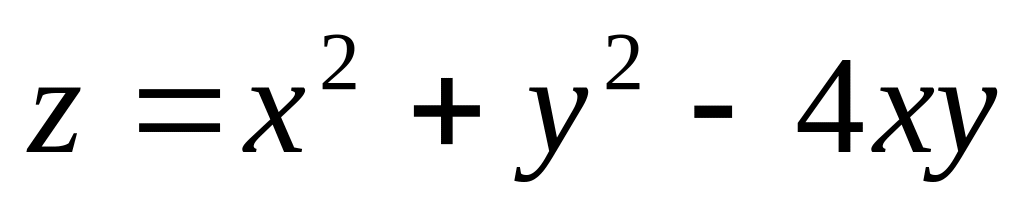 и
и
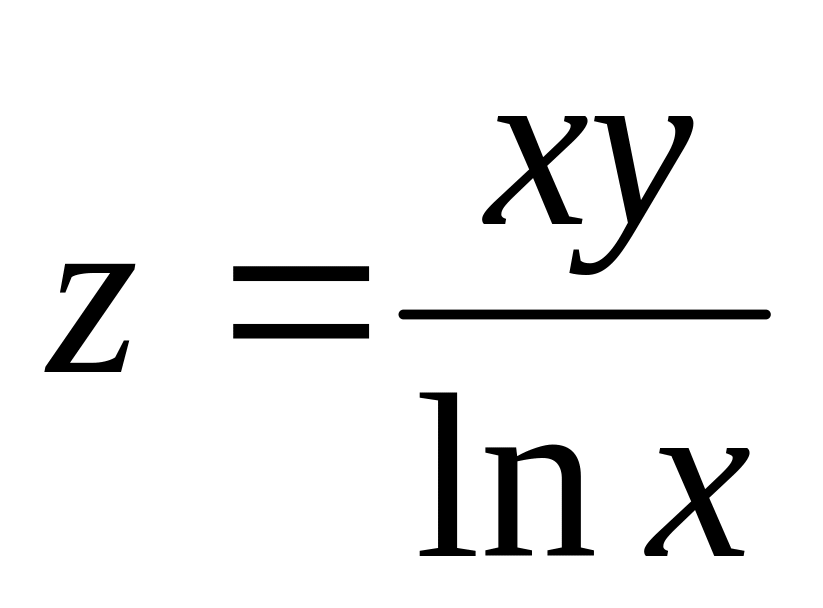 по переменной х имеют вид…
по переменной х имеют вид…
Ответ: 1) 2x
– 4y;
![]() ;
2) 2x – xy;
;
2) 2x – xy;
![]() ;
3) 2x – 2y;
;
3) 2x – 2y;
![]() ;
4) 2x + 4y;
;
4) 2x + 4y;
![]() ;
;
Частная производная функции

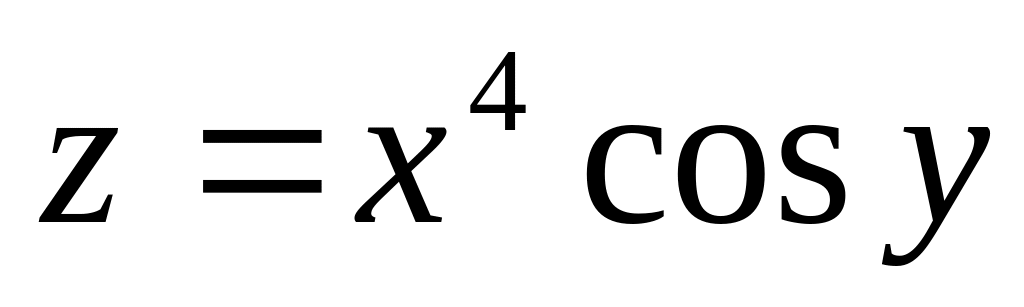 по переменной у в точке
по переменной у в точке
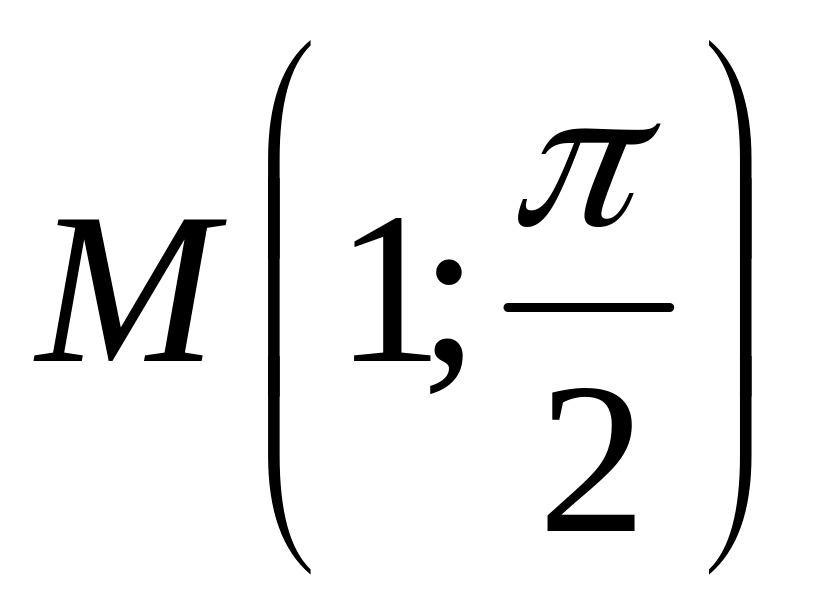 равна …
равна …
Ответ: 1) 0; 2) 4; 3) 1; 4) -1.
Дифференциальное уравнение
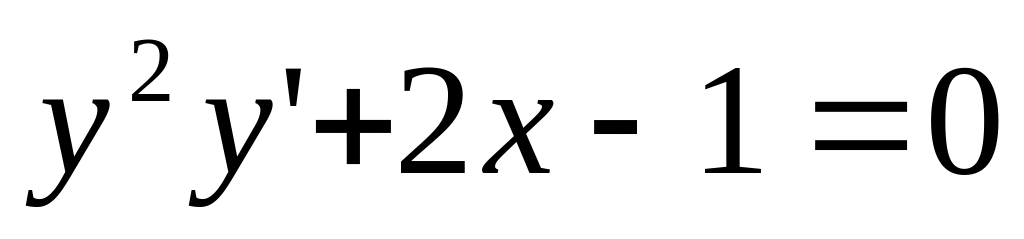 является ….
является ….
Ответ: 1) уравнением Бернулли; 2) линейным неоднородным дифференциальным уравнением; 3) однородным дифференциальным уравнением; 4) уравнением с разделяющимися переменными.
Дано дифференциальное уравнение
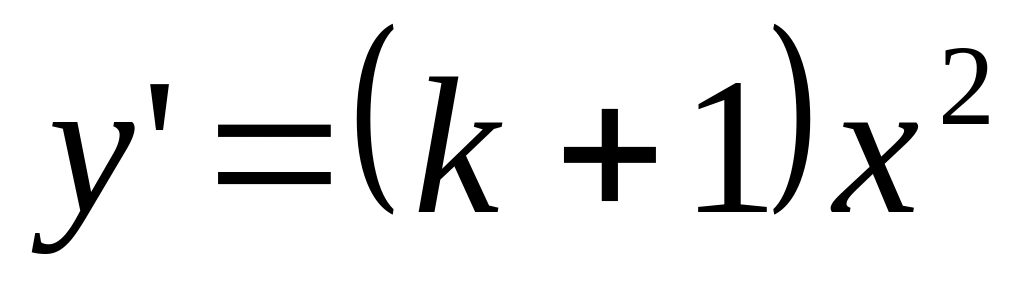 ,
тогда функция
,
тогда функция
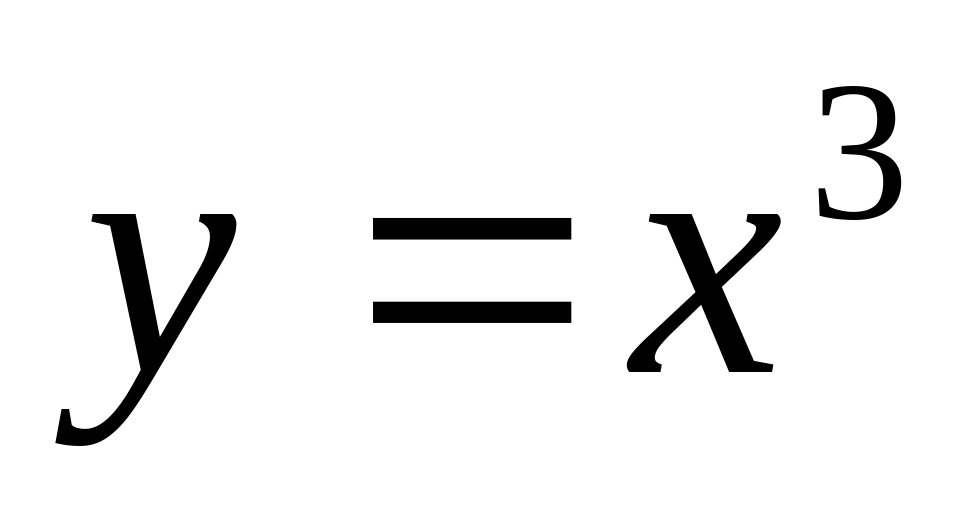 является его решением при
является его решением при
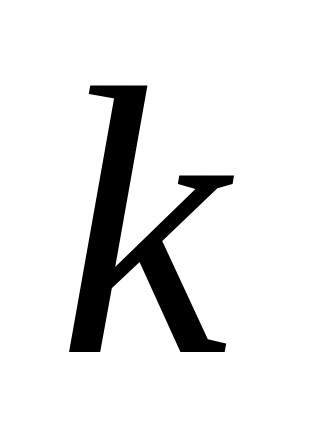 равно…
равно…
Ответ: 1) 1; 2) 0; 3) 2; 4) 3.
Общее решение линейного однородного дифференциального уравнения
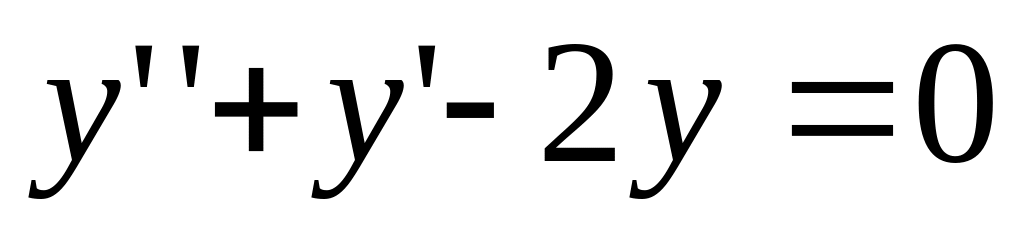 имеет
вид…
имеет
вид…
Ответ: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() 4)
4)
![]()
частному решению линейного неоднородного дифференциального уравнения
 по виду его правой части соответствует
функция…
по виду его правой части соответствует
функция…
Ответ: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Интегральная кривая, соответствующая уравнению y’= x и удовлетворяющая начальному условию
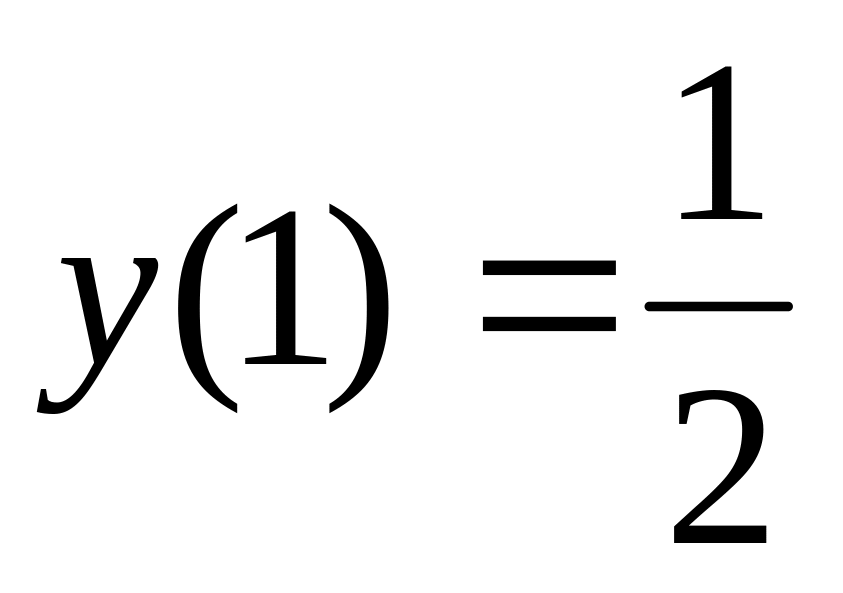 изображена графиком…
изображена графиком…
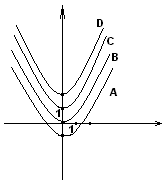
Ответы 1) D; 2) B; 3) C; 4) A
Решения уравнения
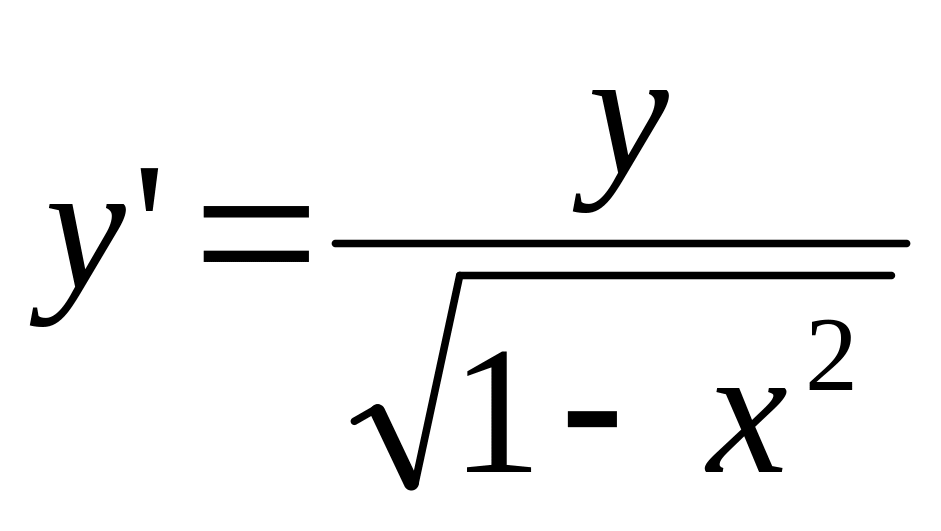 имеет вид….
имеет вид….
Ответ: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
21) Из уравнений
A)
![]()
B)
![]()
C)
![]()
D)
![]() дифференциальными являются …
дифференциальными являются …
Ответы:
1) все уравнения;
2) уравнения A, B, C;
3) уравнения A, B, D;
4) уравнения A, B.
22) Являются ли решением данных дифференциальных уравнений указанные функции:
A)
![]()
B)
![]()
Ответы:
1) A - является, B – не является;
2) A и B - являются;
3) A и B – не являются;
4) A – не является, B является.
23) Дано дифференциальное
уравнение
![]() ,
тогда функция
,
тогда функция
![]() является его решением при k равном …
является его решением при k равном …
Ответы:
1) 1;
2) 0;
3) 2;
4) 3.
24) Интегральная
кривая, соответствующая уравнению
![]() и удовлетворяющая начальному условию
и удовлетворяющая начальному условию
![]() изображена графиком …
изображена графиком …
Ответы:
1) D;
2) A;
3) B;
4) C.
25) Уравнение
![]() является …
является …
Ответы:
1) Уравнением Бернулли;
2) линейным неоднородным уравнением;
3) однородным дифференциальным уравнением;
4) дифференциальным уравнением с разделяющимися переменными;
26) Уравнение
![]() является …
является …
Ответы:
1) Уравнением Бернулли;
2) линейным неоднородным уравнением;
3) линейным однородным уравнением;
4) уравнением с разделяющимися переменными;
27) Решением уравнения
с разделяющимися переменными
![]() является …
является …
Ответы:
1)![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
28) Являются ли дифференциальные уравнения
A)
![]()
B)
![]()
уравнениями в полных дифференциалах?
Ответы:
1) A – не является, B – является;
2) A и B – не являются;
3) A и B – являются;
4) A – является, B не является.
29) Решением
однородного уравнения
![]() при
при
![]()
является …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
30) Решением линейного
неоднородного уравнения
![]() ,
удовлетворяющим условию
,
удовлетворяющим условию
![]() является …
является …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
31) Интеграл уравнения
![]() имеет вид …
имеет вид …
Ответы:
1) ;
2) ;
3)
![]() ;
;
4) ;
32). Дано линейное
однородное дифференциальное уравнение
![]() .
Тогда его общее решение имеет вид …
.
Тогда его общее решение имеет вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
33) Общее решение
линейного однородного уравнения
![]() имеет вид …
имеет вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
34) Частному решению
линейного неоднородного дифференциального
уравнения
![]() по виду его правой части соответствует
функция …
по виду его правой части соответствует
функция …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
35) Частное решение
уравнения
![]() будем искать в виде …
будем искать в виде …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
36) Решение
дифференциального уравнения
![]() имеет вид …
имеет вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
37). Решением
дифференциального уравнения
![]() является …
является …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
38) Решение уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() имеет вид …
имеет вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
39). Общее решение
системы уравнений
![]() имеет
вид …
имеет
вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
40) Общим решением
системы уравнений
![]() является …
является …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
41). Общее решение
однородной системы
![]() имеет вид …
имеет вид …
Ответы:
1)
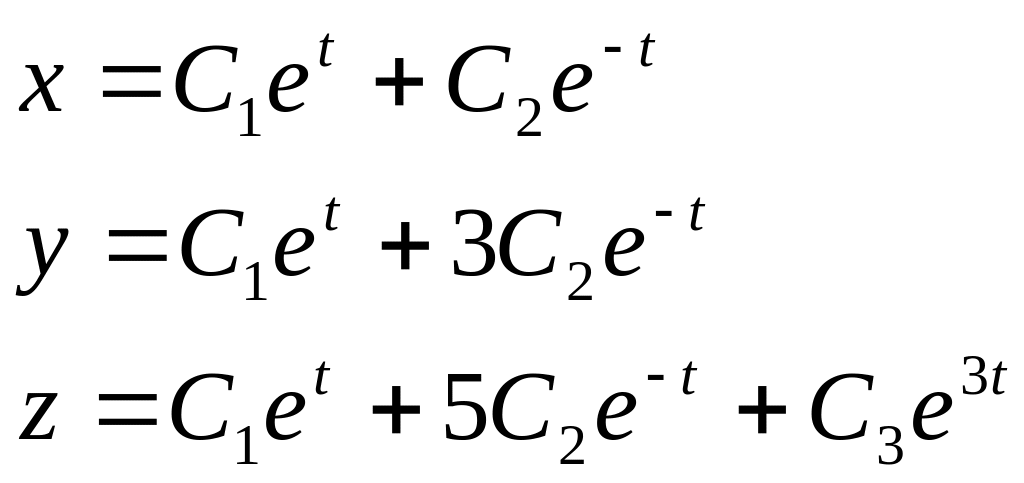 ;
;
2)
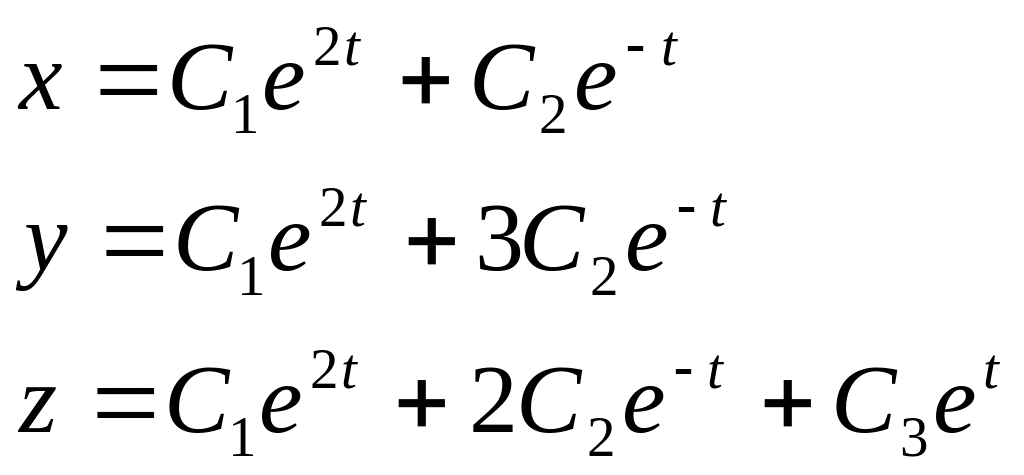 ;
;
3)
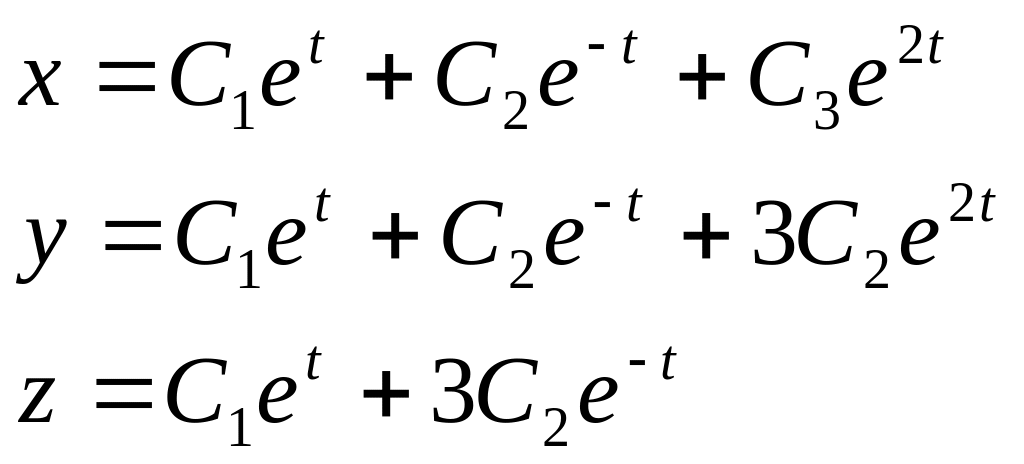 ;
;
4)
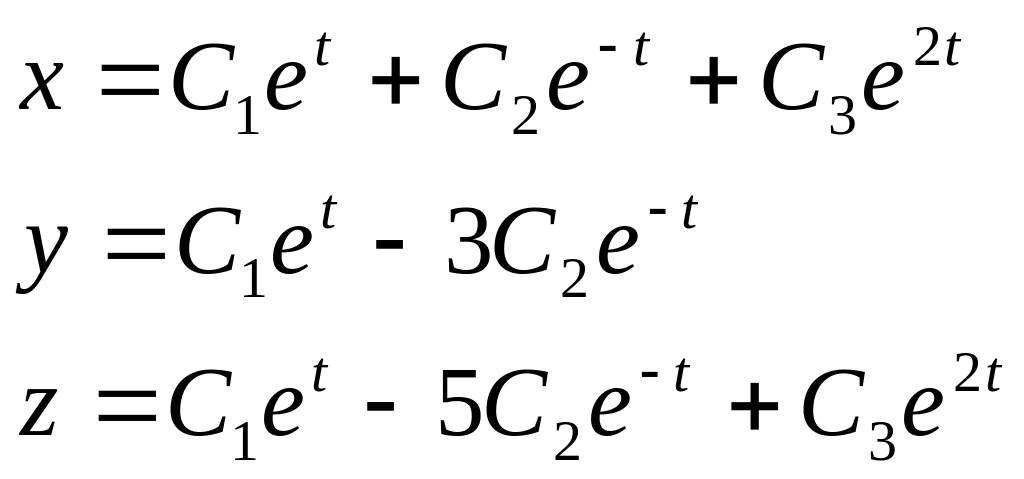 ;
;
42). Общее решение
неоднородной системы
![]() имеет вид …
имеет вид …
Ответы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
