6. Границы случайной погрешности

Доверительные границы случайной погрешности вычисляются при доверительной вероятности P = 0,95, а также при P = 0,99, если измерения в дальнейшем повторить нельзя:

, (1.19)

где t_p – коэффициент Стьюдента, определяемый по табл. П.4 при заданной доверительной вероятности P и числе степеней свободы k. Для прямых измерений

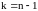. (1.20)

7. Границы неисключенной систематической погрешности

В качестве составляющих неисключенной систематической погрешности рассматриваются погрешности метода, погрешности средств измерений (например, пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение, и тогда границы неисключенной систематической погрешности результата при числе составляющих m > 4 определяют как

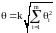, (1.21)

где – границы отдельных составляющих общим числом m;

k – коэффициент, равный 1,1 при доверительной вероятности P = 0,95 и 1,4 при P = 0,99. Если же число суммируемых погрешностей m  4, то коэффициент k определяется по графику (рис. 1.1).

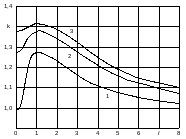
Рис. 1.1. График зависимости

1 – m = 2; 2 – m = 3; 3 – m = 4;

При трех или четырех слагаемых в качестве ₁ принимается составляющая, по числовому значению наиболее отличающаяся от других, в качестве ₂ следует принять ближайшую к ₁ составляющую.

8. Граница погрешности результата измерения

Если выполняется условие

, (1.22)

то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата

. (1.23)

Если

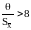, (1.24)

то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата

. (1.25)

Если оба условия (1.22) и (1.24) не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины:

, (1.26)

где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей:

; (1.27)

S_ – оценка суммарного среднеквадратического отклонения результата измерения:

. (1.28)

9. Запись результата

Окончательный результат измерений записывается в виде:

, P. (1.29)

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности .

2. Ход работы

Выполним для примера обработку результатов 20 измерений температуры термометром с точностью ±1,0 °C, не содержащих систематическую погрешность, сведенных в табл. 1.2.

Таблица 1.2

Результаты измерений температуры

Xi	Xi	Xi	Xi	Xi
32,1	36,5	32,5	30,3	29,5
34,3	37,7	34,7	40,4	26,4
34,3	43,6	35,3	34,6	38,7
35,4	34,1	35,6	33,7	31,4

1. Исключаем систематическую погрешность. Так как по условиям эксперимента систематическая погрешность отсутствует, то поправки вносить не следует, исправленные результаты измерений совпадают с неисправленными X_i.

2. Находим оценку математического ожидания (1.2):

.

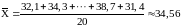Результаты всех промежуточных расчетов должны содержать 1 – 2 лишних десятичных знака относительно точности исходного массива.

3. Среднеквадратическое отклонение (1.3):

.

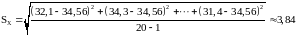Среднеквадратическое отклонение среднего арифметического (1.4):

.

4. Проверка закона распределения на нормальность. Так как число измерений менее 40, то в качестве критерия следует применять составной критерий.

Критерий 1. Находим смещенное среднеквадратическое отклонение по (1.12):

.

Находим квантиль d по (1.11):

.

По табл. П.2 при уровне значимости q₁ = 0,02 и числе измерений 20 находим с использованием линейной интерполяции:

; .

Так как неравенство (1.13) соблюдается:

,

то критерий 1 выполняется.

Критерий 2. По табл. П.3 при уровне значимости q₂ = 0,02 определяем:

m = 1;  = 0,99.

Применяя (1.16) и табл. П.6 находим для :

.

Ширина интервала по (1.15):

.

Ни одна из разностей (1.14) не превзошла пороговую величину 9,9, следовательно, критерий 2 выполняется.

Таким образом, с уровнем значимости % гипотеза о нормальности полученных данных принимается.

5. Проверка на промахи. Подозрительными на промах являются значения и . Для них по (1.5):

; .

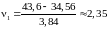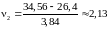По табл. П.6 при n = 20 и q = 5 % определяем граничное значение :

.

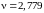Так как и , то ни , ни промахом не являются.

6. Границы случайной погрешности. По табл. П.4 при числе степеней свободы k = 20 – 1 = 19 определяем t_p для двух доверительных вероятностей p:

t_p = 2,093 при p = 0,95;

t_p = 2,861 при p = 0,99.

Границы случайной погрешности определяются по (1.19):

при p = 0,95;

при p = 0,99.

7. Граница неисключенной систематической погрешности определяется по (1.21). Так как по условию задачи есть только одна неисключенная систематическая погрешность, то

.

8. Чтобы найти границу погрешности результата измерения, необходимо проверить условия (1.22) и (1.24), где . Таким образом, оба условия не соблюдаются, и для расчета границы погрешности результата измерения следует воспользоваться формулой (1.26) для двух доверительных вероятностей p:

при p = 0,95;

при p = 0,99.

9. При записи результата производится округление до первоначальной точности исходного массива чисел:

°C при p = 0,95;

°C при p = 0,99.