Нелинейное программирование Постановка и особенности задач нелинейного программирования

К задачам нелинейного программирования относятся такие задачи, в которых или целевая функция, или система ограничений, или и целевая функция и система ограничений содержат выражения, нелинейные относительно переменных. Такого рода задачи возникают на практике в тех случаях, когда, например, затраты растут не пропорционально количеству произведенной или закупленной продукции.

Задачи нелинейного программирования можно классифицировать в соответствии с видом целевой функции f(Х), функциями ограничений и количеством переменных в задаче (размерностью вектора решений Х).

Обобщенно классификация может быть представлена в следующем виде:

Таблица 1

Классификация задач нелинейного программирования

Вид функции f(Х)	Вид функций ограничений	Число переменных	Название задачи
Нелинейная	Отсутствуют	Одна	Безусловная однопараметрическая оптимизация
Нелинейная	Отсутствуют	Более одной	Безусловная многопараметрическая оптимизация
Нелинейная	Нелинейные или линейные	Более одной	Условная нелинейная оптимизация
Линейная	Нелинейные	Более одной	Условная нелинейная оптимизация

В общем виде задача нелинейного программирования формулируется так:

найти значения вектора Х переменные x_j ( j=1÷ n ), при которых f(X) =

= f(x₁, x₂, …,x_n)max (min)

при ограничениях g_i(x₁, x₂, …,x_n) ≤ (≥, =) a_i0, i=1÷m;

где f и g - заданные функции от n переменных.

Для задач нелинейного программирования, в отличие от линейных задач, нет универсального метода решения. Напомним некоторые свойства задач линейного программирования:

• множество допустимых решений выпукло. Это выпуклое множество имеет конечное число вершин, которые обычно называют крайними или угловыми точками;

• целевая функция, принимая определенное значение, представляет собой гиперплоскость (линию) уровня. Все гиперплоскости (линии) уровня, соответствующие разным значениям целевой функции, параллельны между собой;

• для задач линейного программирования не существует понятий локального максимума (минимума) и глобального. На множестве допустимых решений локальный оптимум является также и глобальным;

• если область допустимых решений ограничена, то задача линейного программирования всегда имеет решение, которое достигается, по крайней мере, в одной из вершин (крайних, угловых точках) множества допустимых решений.

В произвольной задаче нелинейного программирования многие перечисленные свойства могут отсутствовать.

Рассмотрим некоторые особенности задач нелинейного программирования.

1. Область допустимых решений не обязательно является выпуклым множеством.

Пример 1. Дана система ограничений:

(x₁ – 2)² + (x₂ – 2)² ≤ 4

(x₁ – 3)² + (x₂ – 3)² ≥ 1

x₁ 0; x₂ 0

и целевая функция maxZ = 1,5x₁+1,5x₂ .

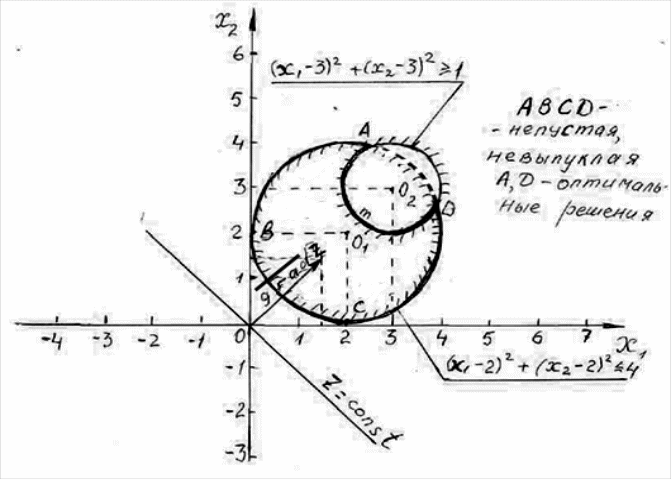
Рис.1. Область допустимых решений - невыпуклое множество

Заменим неравенство на равенство: (x₁ – 2)² + (x₂ – 2)² = 4. Данное выражение геометрически представляет собой окружность с центром в точке с координатами (2; 2) и радиусом, равным =2.

Аналогично со вторым ограничением: (x₁ – 3)² + (x₂ – 3)² =1. Строим окружность с центром в точке (3; 3) и радиусом, равным 1.