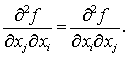Рекомендуемая литература

А

Абсолютный минимум – функция имеет в точке абсолютный (глобальный) минимум, если выполняется неравенство , где - любая точка, принадлежащая области определения функции.

Абсолютный максимум - функция имеет в точке абсолютный (глобальный) максимум, если выполняется неравенство , где - любая точка, принадлежащая области определения функции.

Разница между локальным и абсолютным максимумами та, что абсолютный максимум достигается во всей области определения, а локальный лишь в окрестности точки.

Антиградиент- вектор Z = Z(X) = Z(x₁, x₂,...,x_n) - выпуклая целевая функция.

В каждой точке области, где определена и дифференцируема функция Z, определяется вектор антиградиент antigrad Z= -iZ/x₁-jZ/x₂- ...-kZ/x_n .

Антиградиент Z может иметь другие обозначения:

antigrad Z = - grad Z= -{Z/x₁;Z/x₂; ...;Z/x_n } или

- grad Z= - Z (набла).

Б

Базисная переменная – переменная, коэффициенты которой образуют единичный столбец.

Базисное решение – система ограничений приведена к единичному базису, свободные переменные равны нулю, а все базисные переменные равны свободным членам.

В

Вейерштрасс теорема Теорема Вейерштрасса. Непрерывная функция, определенная на ограниченном, замкнутом множестве, в одной из точек множества принимает максимальное (минимальное) значение.

Вектор градиент - Z = Z(X) = Z(x₁, x₂,...,x_n) - выпуклая целевая функция.

В каждой точке области, где определена и дифференцируема функция Z, определяется градиент grad Z= iZ/x₁+jZ/x₂+ ...+kZ/x_n .

Градиент Z может иметь другие обозначения:

grad Z= {Z/x₁;Z/x₂; ...;Z/x_n } или grad Z= Z (набла).

Вогнутая функция. Функция называется вогнутой (выпуклой вниз) на промежутке Х, если для любых двух значений х₁ и х₂, принадлежащих промежутку Х, выполняется неравенство f[(х₁ + х₂)/2]  [f(х₁) + f(х₂)] /2.

Вогнута функция (выпукла вниз) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке Х монотонно возрастает (теорема). Геометрически – угол наклона касательных к графику функции возрастает. Дуга между точками на кривой f (X), выражающей вогнутую (выпуклую вниз) функцию, всегда лежит ниже прямой, соединяющей эти точки (секущей).

Выпуклое множество Множество  называется выпуклым, если для любых двух несовпадающих точек найдется отрезок прямой, соединяющий эти точки и целиком принадлежащий множеству .

Выпуклое множество. Пусть функции - выпуклые. Тогда множество , определяемое условиями :

является выпуклым множеством, так как пересечение выпуклых функций - выпуклое множество, если оно непустое

Выпуклое программирование. Задачи выпуклого программирования – это задачи минимизации нелинейной, но гладкой функции выпуклой или вогнутой при ограничениях, заданных нелинейными или линейными неравенствами, определяющими выпуклое множество.

Если задача имеет выпуклую целевую функцию и выпуклую систему ограничений, то такая задача называется выпуклой задачей математического программирования.

Задача выпуклого программирования, если и - выпуклые функции, .

Выпуклая функция. Функция называется выпуклой на выпуклом множестве , если она обладает следующим свойством где ; ; - выпуклое множество.

Выпуклые функции не имеют перемежающихся подъемов и спусков, и, следовательно, локальных экстремумов. Дуга между точками на кривой f (X), выражающей выпуклую функцию, всегда лежит выше ниже прямой, соединяющей эти точки.

Выпуклая функция. Функция называется выпуклой (выпуклой вверх) на промежутке Х, если для любых двух значений х₁ и х₂, принадлежащих промежутку Х, выполняется неравенство f[(х₁ + х₂)/2]  [f(х₁) + f(х₂)] /2.

Выпукла функция (выпукла вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке Х монотонно убывает (теорема). Геометрически – угол наклона касательных к графику функции убывает. Дуга между точками на кривой f (X), выражающей выпуклую (выпуклую вверх) функцию, всегда лежит выше прямой, соединяющей эти точки (секущей).

Выпуклые и гладкие функции (свойства).

Выпуклые функции не имеют перемежающихся подъемов и спусков, и, следовательно, локальных экстремумов. Дуга между точками на кривой f (X), выражающей выпуклую функцию, всегда лежит выше ниже прямой, соединяющей эти точки.

1. Если умножить выпуклую функцию на (-1), то функция вогнутая и наоборот.

2. Сумма конечного числа выпуклых функций - выпуклая функция.

- невыпуклые функции

, , , - выпуклые функции

- выпуклая функция, так как является суммой конечного числа выпуклых функций.

3. Пусть функции

- выпуклые. Тогда множество , определяемое условиями :

является выпуклым множеством, так как пересечение выпуклых функций - выпуклое множество, если оно непустое.

Г

Гессе матрица —матрица вторых частных производных функции нескольких переменных

Гессианом называется определитель этой матрицы. Характеристика гессиана матрицы . (ее отрицательная или положительная определенность и полуопределенность) служит условием для определения вида стационарной точки: является ли она соответственно максимумом, минимумом или седловой точкой в задаче оптимизации функции

Гладкая функция. Гладкость функций означает непрерывность ее первых производных или существование и непрерывность ее частных производных первого порядка.

Градиент — вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении: где символами e_i обозначены единичные векторы осей координат (орты).

Д

Дифференцирование функции — операция определения производной рассматриваемой функции. Например, производная линейной функции (bx + a)′ = b, т. е. является константой; производная степенной функции (xⁿ)′ = nx ^n-1 .

Дифференцируемая функция — функция, имеющая в каждой точке области, на которой она определена, полный дифференциал, а в случае функции одной переменной — производную.

Операция нахождения производных называется дифференцированием функции. Функция, имеющая производную в точке x₀, называется дифференцируемой в этой точке, причем она обязательно непрерывна в этой точке. Функция, имеющая непрерывную производную в каждой точке некоторого интервала, называется непрерывно дифференцируемой на этом интервале (промежутке).

И

Итеративные методы решения оптимизационных задач — заключаются в том, что вычислительный процесс начинают с некоторого пробного (начального, произвольного) допустимого, а затем применяют алгоритм, обеспечивающий последовательное улучшение этого решения. Процесс таких проб продолжается до тех пор, пока не станет ясно, что либо дальнейшее улучшение решения невозможно (достигнут оптимум, причем во многих случаях требуется дополнительно проверить — локалиный или глобальный), либо дальнейшие вычисления нецелесообразны, поскольку возможное улучшение результата не окупит дополнительных затрат. (В последнем случае для определения момента окончания вычислений используется прием, называемый методом Лас-Вегаса.)

Алгоритмы, применяемые при этом (итеративные алгоритмы методов последовательного улучшения плана), можно разделить на три класса:

1) при которых известно, что на каждой итерации решение улучшается, причем число таких итераций для достижения оптимума конечно;

2) при которых также каждая итерация улучшает решение, но оптимум достигается лишь как предел бесконечной последовательности решений (бесконечного вычислительного процесса);

3) алгоритмы, основанные на методе проб и ошибок, обеспечивают улучшение решения в целом, но не на отдельной итерации.

К

Квадратичное программирование — раздел выпуклого программирования: совокупность методов решения экстремальных задач, в которых целевая функция (критерий) представляет собой многочлен второй степени, а ограничения линейны. В матричной форме может быть записана следующим образом:

min Z=f(X) = Z(x₁, x₂, ... , x_n) = C₁₁ x₁² + C₁₂ x₁x₂ + C₁₃ x₁x₃ +...+ C_1nx₁x_n + C₂₂ x₂² + C₂₃ x₂x₃ +...+ C_2nx₂x_n +... + C_nn x_n² + C₁ x₁ + C₂ x₂ +...+ C_nx_n + C₀

.

Квадратичное программирование. Задача называется задачей квадратичного программирования, если целевая функция содержит переменные во второй степени, а система ограничений - линейные выражения. Задачи выпуклого программирования делятся на общую задачу выпуклого программирования, специальную задачу выпуклого программирования и задачу квадратичного программирования.

Квадратичного программирования задача имеет квадратичную целевую функцию и линейную систему ограничений.

min Z=f(X) = Z(x₁, x₂, ... , x_n) = C₁₁ x₁² + C₁₂ x₁x₂ + C₁₃ x₁x₃ +...+ C_1nx₁x_n + C₂₂ x₂² + C₂₃ x₂x₃ +...+ C_2nx₂x_n +... + C_nn x_n² + C₁ x₁ + C₂ x₂ +...+ C_nx_n + C₀

Может быть построена и двойственная задача квадратичного программирования.

Конечные методы математического программирования — численные методы, позволяющие получить решение задачи за определенное (не обязательно известное заранее) количество шагов (итераций).

Куна-Таккер теорема. Теорема Куна –Таккера (для седловой точки).

Пусть задана область решений задачи выпуклого программирования где выпуклые функции, .

Если эта область имеет внутренние точки, то есть выполняется условие Слейтера: существует решение X , такое, что _i(X) < 0 для всех i, i = 1  m. Тогда для того чтобы X* было оптимальным решением задачи, необходимо и достаточно, чтобы существовал неотрицательный m-мерный вектор λ*(λ*₁,λ*₂,…,λ*_m) такой, что пара (X*, λ*) является седловой точкой функции Лагранжа. , где ≥0 можно записать в виде неравенств, т.е.

f(X)+ λ*_i·_i(X) ≥ f(X*)+ λ*_i ·_i(X*) ≥ f(X*)+ λ_i ·_i(X*), i = 1  m.

λ_i≥0, i = 1  m.

Кусочно-линейные приближения — метод решения задач нелинейного программирования (главным образом выпуклого программирования) путем предварительной линейной аппроксимации целевой функции и ограничений, т. е. их замены близкими к ним кусочно-линейными функциями.. Это означает, что кривая данной функции заменяется вписанными в нее ломаными прямыми линиями. Полученная приближенная задача решается с помощью методов линейного программирования.

Кусочно-линейная функция— нелинейная функция f(x) = f(x₁, x₂, ..., x_n), которая (при ее геометрическом представлении) состоит из переходящих друг в друга линейных участков. Любая функция от одного аргумента, непрерывная в замкнутом интервале, может быть с заданной точностью аппроксимирована кусочно-линейная функция.

Л

Лагранжа метод — метод решения ряда классов задач математического программирования с помощью нахождения седловой точки (x*, λ*) функции Лагранжа, что достигается приравниванием нулю частных производных этой функции по x_i и λ_i. , где λ_{i –} множители, i = 1 m.

Лагранжа множители — дополнительные множители, преобразующие целевую функцию экстремальной задачи выпуклого программирования (в частности, линейного программирования) при ее решении одним из классических методов — методом разрешающих множителей (методом Лагранжа). Полученная функция носит название лагранжиан, или функция Лагранжа.

Локальное свойство функции показывает степень ее гладкости, т.е показывает свойства, связанные с непрерывностью функции, существованием и непрерывностью ее частных производных по направлению.

Локальный максимум. Функция в точке имеет локальный максимум, если у точки имеется окрестность любого, в том числе и бесконечно малого радиуса , для которого выполняется неравенство , где - любая точка, принадлежащая окрестности.

Локальный экстремум. Теорема о совпадении локального экстремума с глобальным (абсолютным). В любой задаче выпуклого программирования любой локальный минимум обязан совпадать с глобальным.

То есть если найден минимум в задаче выпуклого программирования, то в задаче найдено оптимальное решение. Этот минимум являеться и глобальным, и локальным.

Локальный случайныйо поиск на минимум целевой функции.

Найти min Z = f( )

при условии а_j ≤ x_j ≤ b_j; j = 1 ÷ n,

где f( )– выпуклая функция.

1. Выписываем область допустимых значений ω( а_j ≤ x_j ≤ b_j ); где j=1÷n.

2. Подготавливаем начальный вектор (а₁, а₂, ..., а_n) = (x_{1нижняя граница}, x_{2нижняя граница},…, x_{nнижняя граница}) = ( x₁⁰, x₂⁰, ..., x_n⁰ ), координатами служат нижние границы измерения координат из области допустимых решений ω.

3. Вводим целевую функцию Z = f( ).

4. Вычисляем целевую функцию при = , Z = f( ).

5. Вводим счетчик неудачных испытаний S = 0, N = 1000 – контрольное число.

6. Формируем массив случайных чисел λ.

7. Формируем случайный вектор , где  , координаты которого вычисляются по формуле: = x_j⁰ +P_j · , где - заданное для данной задачи число, например, если =1, то = + · 1. Вектор сам является случайным вектором, координаты которого принадлежат какому-то заданному интервалу,

≤ P_j ≤ . Например, интервалу . Координаты вектора формируются по формуле P_j =A+ λ_jּB, где λ_j - число из массива случайных чисел λ.

8. Следовательно, x_j¹ = x_j⁰ + (A+ λ_jּB) · .В этой задаче можно значение менять по формуле = до какого-то заданного предела .

9. Вычисляем целевую функцию при = , Z = f( ).Сравниваем f( ) и f( ).

10. Если испытание удачное, то есть если f( ) <f( ), то переход к пункту 11, иначе переход к пункту 12.

11. = и Z =f( ) = f( ).Переход к пункту 7.

12. Если f( ) ≥ f( ), то ведем счет неудачных испытаний

S = S + 1.

13. Сравниваем S и N, где N – контрольное число неудачных испытаний.

14. Если S ≤ N, то переходим к пункту 7, иначе переход к пункту 15.

15. Конец вычислений. Запись ответа Z = f( ) и .

М

Минор элемента a_ij матрицы (n)-ого порядка - определитель (n-1) порядка, полученный вычеркиванием i-ой строки и j-го столбца в исходной матрице.

Н

Наискорейший подьем (рост), наискорейший спуск — направления поиска экстремума (максимальной или минимальной точек) в задачах нелинейного (математического) программирования при их решении градиентными методами.

Нелинейность, нелинейная функция — термины, относящиеся к зависимостям, графики которых не являются прямыми линиями.

Нелокальный случайный поиск на минимум целевой функции

Найти min Z = f( )

при условии а_j ≤ x_j ≤ b_j; j = 1 ÷ n,

где f( )– выпуклая функция

1. Выписываем область допустимых значений ω( а_j ≤ x_j ≤ b_j ); где j=1÷n.

2. Подготавливаем начальный вектор (а₁, а₂, ..., а_n) =

= (x_{1нижняя граница}, x_{2нижняя граница},…, x_{nнижняя граница}) =

= ( x₁⁰, x₂⁰, ..., x_n⁰ ), координатами служат нижние границы измерения координат из области допустимых решений ω.

3. Вводим целевую функцию Z = f( ).

4. Вычисляем целевую функцию при = , Z = f( ).

5. Вводим счетчик неудачных испытаний S = 0, N = 1000 – контрольное число.

6. Формируем массив случайных чисел λ.

7. Формируем случайный вектор , где  , координаты которого вычисляются по правилу x_j¹ = x_{j нижняя граница} + λ_j ּx_{jверхняя граница} = а_j + λ_j ּb_j.

8. Вычисляем целевую функцию при = , Z = f( ).

9. Сравниваем f( ) и f( ).

Если испытание удачное, то есть если f( ) <f( ), то переход к пункту 11, иначе переход к пункту 12.

10. = и Z =f( ) = f( ).

Переход к пункту 7.

11. Если f( ) ≥ f( ), то ведем счет неудачных испытаний S = S + 1.

12. Сравниваем S и N, где N – контрольное число неудачных испытаний. Если S ≤ N, то переходим к пункту 7, иначе переход к пункту 13

13. Конец вычислений. Запись ответа Z =f( ) и .

Непрерывная функция — во-первых, функция называется непрерывной в точке M₀, если для любого числа ε > 0 можно указать окрестность S_r(M₀) (S точки M₀) так, что для всех точек M  S выполняется неравенство |f(M) – f(M₀) |< ε; а во-вторых, функция f(M) называется непрерывной на множестве V, если она непрерывна в каждой точке этого множества.

Или непрерывность функции означает, что в результате небольшого изменения значения аргумента в любой точке области определения функции значение функции также изменится мало.

Ньютона метод— вычислительный алгоритм решения широкого класса экстремальных задач (на отыскание безусловного минимума функции), использующий вторые частные производные минимизируемой функции. Обладает сравнительно быстрой сходимостью (искомая точка достигается через небольшое число итераций), но требует трудоемких вычислений.

О

Общая задача выпуклого программирования имеет выпуклую целевую функцию и систему ограничений, состоящую из выпуклых функций.

min Z=f(X)

φ_i(X) ≤ 0, i=1m,

x_j ≥0; j=1n,

где f(X) – выпуклая функция,

φ_i(X), i=1m – выпуклые функции.

Ограничение – это математическое выражение, связывающее переменные в виде равенств или неравенств. Все ограничения образуют систему ограничений задачи. Ограничения бывают трех типов: равенства (=), неравенства типа меньше либо равно ( ), неравенства типа больше либо равно ( ).

Определитель матрицы, детерминант — число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A): det A. Например, определитель (второго порядка) матрицы

обозначается и вычисляется следующим образом:

det A = a₁₁a₂₂ — a₁₂a₂₁.

Оптимальное решение – решение, в котором достигается экстремум (максимум или минимум) целевой функции.

П

Поиска метод. Все методы решения, основанные на исследоваии функций в небольшой окрестности последовательно выбираемых точек, называют методами поиска. Следует отметить, что все методы поиска - вычислительные, а следовательно, проводятся с ограниченной точностью. Методы поиска весьма разнообразны и включают целый ряд различных алгоритмов.

Производная. Для функции от одной переменной f(x) — производная df/dx — это скорость ее изменения, т. е.

Необходимы различные обобщения этого понятия на более сложные функции. Например, если рассматривается функция многих переменных f (x₁, ..., x_n), то оказывается возможным использовать производные по одной из них (принимая остальные за неизменные). Такая производная называется частной и обозначается df/dx. Любая частная производная есть в свою очередь функция переменных x₁, ..., x_n — поэтому можно рассматривать вторые частные производные

Важное свойство вторых частных производных — их симметричность; если функция f непрерывна, имеет непрерывные первую и вторую частные производные, то безразлично, в каком порядке функцию дифференцировать:

Кроме обозначения производных, указанного выше, используется штрих ′ или апостроф ', например, производная функции f(x) обозначается либо df / dx, либо f′(x).

Производная частная — понятие дифференциального исчисления: производная функции нескольких переменных по одной из них. Характеризует скорость изменения функции, когда меняется только один аргумент, а все остальные принимаются неизменными.

С

Седловой точкой действительной функции f (x,y), определённой для всех x  A, y B, называется точка (x₀ , y₀ ), где x₀  A, y₀  B, если выполнены следующие условия:

1. x  A, f (x , y, x₀, y₀), f (x₀ , y₀), f (x, y).

2. x В, f (x , y, x₀, y₀), f (x₀ , y₀), f (x, y).

Специальная задача выпуклого программирования имеет выпуклую целевую функцию и линейную систему ограничений.

min Z=f(X) = Z(x₁, x₂, ... , x_n)

, где f(X) – выпуклая функция.

Стационарная точка - точка X* , в которой все частные производные функции Z = f (Х) равны 0.

Ц

Целевая функция - Z = f (Х) - математическое выражение, для которого требуется найти экстремальное (то есть максимальное или минимальное) значение. Целевую функцию называют также функционалом. Целевая функция математически записывает критерий оптимальности, критерий качества.

Ш

Штраф за дефицит - это убытки, связанные с отсутствием запаса

Штрафные функции — вспомогательные функции, применяемые при численном решении некоторых классов задач математического программирования; метод штрафных функций основан на сведении задачи с ограничениями к задаче без ограничений. Например, может быть построена штрафная функция, равная нулю в допустимой области и быстро возрастающая вне ее. После этого решается задача минимизации суммы штрафных функций и целевой функции исходной задачи с помощью одного из известных вычислительных алгоритмов.

Штрафная функция – это вспомогательныя функция - взвешенная сумма квадратов невязок, т.е. штраф за невыполнение ограничений Задача с ограничениями в этом случае сводится к задаче без ограничений.